El producto escalar se comprende mas fácilmente cuando se estudian sus propiedades geométricas a partir de las definiciones de suma y diferencia de vectores.
Por ejemplo, al calcular la magnitud del vector 
en función de las componentes de A y B de acuerdo con la Figura 1 se obtiene la siguiente relación:
en función de las componentes de A y B de acuerdo con la Figura 1 se obtiene la siguiente relación:
La misma distancia se puede obtener geométricamente por el teorema del coseno:
Figura 1. Diferencia de vectores
Dado que es la misma distancia obtenida por dos procedimientos diferentes, se hace evidente la igualdad:
La cual se puede reducir de forma algebraica como sigue:
Esto es equivalente a:
Cuando se cancelan los factores comunes a ambos lados de la igualdad se llega a la ecuación mas conocida del producto escalar de vectores:
Ecuación 1 Producto escalar de dos vectores
Esta ecuación resulta de gran utilidad porque permite calcular el producto escalar a través de las componentes, al tiempo que permite calcular el ángulo formado entre dos vectores sin necesidad de hacer abstracción geométrica de los mismos.
Como se puede deducir de la Ecuación 1, el producto escalar de un vector por si mismo es igual al cuadrado de su magnitud.
Ecuación 2 Producto escalar de un vector por si mismo.
El producto escalar cumple además la propiedad distributiva del producto con respecto a la suma.
Ecuación 3 Propiedad distributiva del producto escalar con respecto a la suma
Como se observa en el Ejemplo 2 , un producto escalar negativo indica que el ángulo entre los vectores implicados se encuentra ubicado en el segundo cuadrante; cuando el producto es positivo, entonces se debe asumir que este se encuentra en el primer cuadrante. Cuando los vectores son ortogonales el producto escalar es nulo.
Las relaciones geométricas enunciadas anteriormente no son las únicas relaciones que se pueden hallar para la completa interpretación del producto escalar.
A partir de dos vectores A y B que se ubican como se muestra en la Figura 1 , es posible deducir otra relación geométrica importante en el producto escalar.
Figura 2. Proyección escalar de un vector sobre otro.
El producto escalar equivale a la relación:
Cuando se usa esta relación se puede calcular la proyección de un vector sobre otro con base en el producto escalar y las proyecciones mostradas en la Figura 2 :
Ecuación 4 Proyección escalar de un vector sobre otro usando el producto escalar.
La interpretación geométrica del producto escalar como proyección de un vector sobre otro resulta altamente útil cuando uno o dos de los vectores se hacen unitarios, en este caso, la magnitud de A o de B se hacen “ 1” y la proyección se reduce simplemente al producto punto de vectores.
Cuando se desea calcular la componente normal o tangencial de un vector sobre una superficie dada, basta con encontrar un vector unitario normal o tangencial a dicha superficie y multiplicarlo mediante producto escalar con el vector deseado.
En física, cuando aplicamos una fuerza a un cuerpo y éste se mueve decimos que hacemos un trabajo.
Sobre un suelo horizontal con un fuerza F trasladamos un peso de 100 kilos a una distancia d.
El producto
nos da el valor del trabajo(T).
El producto
nos da el valor del trabajo(T).
Esto quiere decir que:
Cuanto más fuerza tenemos que hacer, el trabajo será mayor.
Cuanto mayor sea la distancia a la que hemos desplazado el cuerpo, mayor será el trabajo que hemos hecho.
Entendemos como trabajo, en Física (mecánica), como el producto de una Fuerza por la Distancia que recorre un cuerpo al que le hemos aplicado la fuerza.
La distancia que recorre es una magnitud vectorial porque tiene una medida –módulo-, una dirección y un sentido.
Lo mismo sucede con la fuerza que hacemos sobre el objeto. Tenemos que indicar de cuanto es el valor de la misma, su dirección y sentido, incluso podemos hablar de su punto de aplicación.
Entendemos como trabajo, en Física (mecánica), como el producto de una Fuerza por la Distancia que recorre un cuerpo al que le hemos aplicado la fuerza.
La distancia que recorre es una magnitud vectorial porque tiene una medida –módulo-, una dirección y un sentido.
Lo mismo sucede con la fuerza que hacemos sobre el objeto. Tenemos que indicar de cuanto es el valor de la misma, su dirección y sentido, incluso podemos hablar de su punto de aplicación.
La fuerza la puedes aplicar en el mismo sentido que el desplazamiento. Tal como aparece en la última figura.
Pero el ángulo que forma la fuerza con el desplazamiento puede variar entre un ángulo de 0º a 90º.
- En el primer caso, el ángulo entre F y d es de 0º.
- En el segundo caso, el ángulo entre F y d es de 22º.
- En el tercer caso, el ángulo entre F y d es de 90º.
¿Puede influir el ángulo en la cantidad de trabajo que tenemos que hacer?
La respuesta es sí.
¿Por qué?
No es lo mismo hacer una fuerza en una dirección distinta a la del desplazamiento.
El valor de la fuerza que actúa sobre el sólido en este caso, no tiene el mismo valor que si las direcciones de la fuerza y desplazamiento coincidieran.
Cuando existe un ángulo entre F y d, tenemos que calcular la fuerza (f) que actúa en el sólido en la misma dirección que su desplazamiento:
Como f es el cateto contiguo, hallamos el coseno de 45º:
La verdadera fuerza que actúa sobre el sólido es f. Es la fuerza que tiene la misma dirección que el desplazamiento.
La fórmula completa del trabajo será:
- El coseno de 30ºvale >0, 8660.
- El coseno de 45º vale 0, 7071.
- El coseno de 70º vale 0, 3421.
- El coseno de 90º vale 0, 0000.
Ves que a medida que aumenta el valor del ángulo, el valor del
Volvemos al origen del tema que estamos tratando.
Producto escalar de dos vectores.
Según vemos, el producto de dos vectores F y d siendo αel ángulo entre ellos es un valor escalar que procede de multiplicar los valores escalares de dichos vectores por el coseno del ángulo.
A partir de ahora, tenemos en cuenta que dos vectores no sean perpendiculares tal como lo hemos considerado hasta ahora.
A partir de ahora, tenemos en cuenta que dos vectores no sean perpendiculares tal como lo hemos considerado hasta ahora.
A los vectores los representamos con letras minúsculas y con una pequeña flecha sobre ellas indicando dirección y sentido: 
.
Sus valores escalares o módulos los representamos:
El valor escalar del vector
.Sus valores escalares o módulos los representamos:
El valor escalar del vector
Es decir, 
Al coseno del ángulo que forman los vectores
lo representamos por 
.Ten en cuenta que
son números reales o escalares. En cambio,
son vectores y los representamos:
El producto escalar de los dos vectores - 
- es:
- es:
Como verás, en la fórmula del Trabajo decíamos que:
y lo que hemos hecho aplicar lo anteriormente explicado.
21.20 Calcula el ángulo formado por los vectores
y 
.Respuesta: 31º Solución: Tomamos la fórmula:
y despejamos: 
Recuerda que los módulos 
valen:
valen:
Sustituyendo los datos conocidos:
que corresponde a un ángulo de 31°21.21 Calcula el ángulo formado por los vectores
y 
.Respuesta: 22º
21.22 ¿Qué ángulo forman los vectores
Respuesta: 42º
Solución:
que corresponde a un ángulo de 42°
DOS MODOS DE CALCULAR EL PRODUCTO ESCALAR DE DOS VECTORES:
Hemos estudiado que el producto escalar de dos vectores:
podemos hacerlo 
De donde obtenemos:
También sabemos que podemos calcular el producto de dos vectores conociendo el ángulo que forman dichos vectores:
Calculamos:
Sustituimos los valores hallados en la fórmula (I):
Representación Gráfica del Producto Escalar
El producto escalar de un vector a⃗ y otro b⃗ , denotado como a⃗ ⋅ b⃗ devuelve un número (escalar) tal que,
donde α es el angulo que forman los vectores a⃗ y b⃗ .
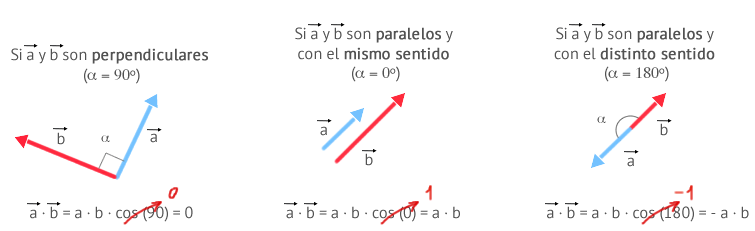
El cálculo del producto escalar de estos dos vectores se simplifica cuando estos son perpendiculares o paralelos entre si:
- Si son perpediculares, el ángulo forma 90º y el producto es 0
- Si son paralelos, tenemos dos posibilidades:
- Si tienen el mismo sentido, el producto escalar es la multiplicación de sus módulos
- Si NO tiene el mismo sentido, el producto escalar es la multiplicación de sus módulos añadiéndole el signo negativo.
Interpretación Geométrica del Producto Escalar
El producto escalar de dos vectores a⃗ y b⃗ no nulos se puede entender como el producto del módulo de b⃗ por el valor de la proyección de a⃗ sobre la recta que define la dirección de b⃗ .
Representación Analítica del Producto Escalar
El producto escalar de dos vectores a⃗ y b⃗ devuelve un escalar que se obtiene como la suma de las multiplicaciones una a una de las componentes cartesianas de los 2 vectores a⃗ y b⃗ . En el caso de vectores en dos dimensiones, podemos usar la expresión:
No hay comentarios:
Publicar un comentario