El magnetismo es una propiedad de la materia que se manifiesta por unas fuerzas de atracción y repulsión. Esta propiedad se pone de manifiesto con determinados minerales, como lamagnetita (mineral de hierro). Los imanes permanentes son barras construidas con minerales naturales o con aleaciones especiales de hierro, cobalto y níquel.
Las propiedades que se observan en los imanes son:
- Todos los imanes poseen dos polos o regiones próximas a sus extremos en las que se concentra la actividad magnética.
- Existen dos tipos de polos magnéticos: uno de ellos se denomina polo norte y el otro se denomina polo sur.
- Los imanes se orientan libremente en la Tierra, de forma que uno de sus polos se orienta siempre hacia el polo norte geográfico (este polo es el que se denomina polo norte magnético). En esta propiedad se basa la utilización de la brújula como instrumento de orientación. De lo anterior se puede deducir que la Tierra se comporta como un imán.
- Polos de idéntico nombre se repelen y polos de distinto nombre se atraen.
- Existen materiales, como el hierro dulce, que son atraídos siempre por cualquiera de los polos de un imán. Este tipo de sustancias se dice que están desimantadas.
- No se han observado nunca polos magnéticos aislados.
La magnetostática es la parte de la física que estudia los fenómenos relativos a los imanes y al campo magnético creado por éstos, así como el comportamiento de los diferentes materiales sometidos a la acción de dicho campo.
En 1820 el físico danés Hans Christian Oersted observó que una aguja magnética o brújula se orientaba en una determinada dirección en las proximidades de un hilo por el que circulaba corriente eléctrica.
La orientación que adquiría la brújula era tal que dependía de la dirección de la corriente eléctrica por el hilo conductor. Esta orientación es siempre perpendicular a la dirección de la corriente eléctrica, y el polo norte de la brújula se orienta en la dirección de los dedos extendidos de la mano derecha, cuando el dedo pulgar está extendido en la dirección de la corriente eléctrica.
el polo sur del imán de las brújulas apunta siempre hacia el norte magnético de la tierra
La experiencia anterior puede realizarse espolvoreando pequeñas limaduras de hierro sobre una cartulina, que es atravesada perpendicularmente por un hilo conductor. Las pequeñas limaduras se orientan formando círculos concéntricos alrededor del hilo conductor.
De las experiencias indicadas es fácil deducir que una corriente eléctrica se comporta como un imán, o expresándolo de otra forma, se puede decir que una corriente eléctrica crea en sus proximidades un campo magnético, entendido este campo como zona en la que se manifiestan efectos magnéticos.
Como la corriente eléctrica es un flujo de cargas eléctricas, entonces, puede afirmarse que el campo magnético no sólo es generado por imanes sino también por la presencia de cargas eléctricas en movimiento ordenado, es decir, por densidades de corriente.
Entonces, puede definirse al campo magnético como la modificación del espacio debido a la presencia de imanes o densidades de corriente.
Si por el momento se consideran a los alambres que transportan corrientes como las fuentes típicas de campos magnéticos y como los objetos típicos sobre los cuales pueden actuar los campos magnéticos, entonces, es posible sugerir que las corrientes generan campos magnéticos y que los campos magnéticos ejercen fuerzas sobre las corrientes.
Ampere formuló la idea de que las propiedades magnéticas de los materiales denominados imanes eran debidas a pequeñas corrientes eléctricas que existían en dichos materiales.
Hoy día se sabe que los electrones de los átomos presentan dos momentos magnéticos debidos a ser una carga eléctrica en movimiento; estos momentos son el magnético de espín y el magnético orbital (debido al movimiento orbital de los electrones).
En general, el valor del campo magnético en las proximidades de un imán o de una corriente eléctrica depende del medio material que rodee al conductor o al imán, debido a la interacción de los momentos magnéticos de los electrones de los átomos del material.
En la actualidad, la relación cuantitativa entre la corriente "I" y la inducción magnética "B" se representa de la siguiente manera:
y se conoce con el nombre de la ley de Ampere. Esta relación indica que la intensidad de un campo magnético sobre un contorno cerrado equivale a la corriente que atraviesa a la superficie limitada por este contorno.
B = m H
H es el campo magnético.
Una manera de demostrar lo anteriormente dicho es haciendo el siguiente análisis:
Por un cable conductor pasa una densidad de corriente G, entonces, la intensidad de corriente eléctrica es
I = ò ò G.dF
La ley de Ampere puede escribirse como:
Por lo tanto
por lo tanto
rot H = G (1)
Todo esto indica que en cada espacio donde existan densidades de corriente existen también rotacionales o remolinos del campo magnético.
Basándose en estas observaciones, es válido decir que no existen cargas magnéticas, pues, el campo magnético es generado por dipolos magnéticos y por lo tanto, su divergencia es nula.
div H = 0
por ser la inducción magnética un vector linealmente dependiente del campo magnético su divergencia también es nula:
div B = 0
Dado que la divergencia del campo magnético es nula, es decir, el campo magnético no tiene fuentes, entonces, este se puede expresar como el rotacional de un campo vectorial libre de fuentes, en otras palabras, como el rotacional de un campo no gradiental.
div B = 0 Þ B = rot A Ù div A = 0 (2)
con (1):
G = rot H Þ m G = rot B
Con (2):
mG = rot rot A Þ mG = -D A (3)
Supóngase el caso en el que el campo magnético es generado por la corriente que fluye a través de un inductor de espiras muy finas. El volumen encerrado por el inductor no contiene densidades de corriente, por lo tanto G = 0.
Ä corriente que entra. · corriente que sale.
Con (1) se obtiene que rot H = 0, por lo tanto el campo magnético puede expresarse como el gradiente de un potencial escalar magnético:
H = -grad Vm
Como el campo magnético no tiene fuentes:
div B = 0 Þ m div (-grad Vm) = 0 Ù \ div grad Vm = 0
D Vm = 0 (4)
esta es la ecuación de Laplace del campo magnético libre de densidades de corriente.
Es preciso resaltar la analogía que se puede establecer entre el campo magnético y el campo eléctrico para observar la dualidad de sus ecuaciones:
CAMPO ELÉCTRICO
|
CAMPO MAGNÉTICO
| |||
rot E = 0
E = -grad V
|
rot H = 0 Þ H = -grad Vm
| |||
Densidad
D = e E
|
Inducción o Densidad
B = m H
| |||
Constante dieléctrica del vació
en el vacío e 0 = 8,85 X 10-12 C/Nm2
|
Permeabilidad magnética del vacío
en el vacío m 0 = 4p · 10-7 Tm/A
| |||
Constante dieléctrica
e = e 0 e r
|
Permeabilidad magnética
m = m 0 m r
| |||
Flujo eléctrico
y e = ò ò D . dF
|
Flujo magnético
y m = ò ò B . dF
| |||
El campo magnético H en las proximidades de un elemento de corriente eléctrica es:
- Directamente proporcional al valor de la densidad de corriente que circula por el hilo, G.
- Inversamente proporcional a la distancia del punto considerado al hilo conductor, r.
En general:
dH = -(1/4p ){G x (1/r3)r}dv
La expresión anterior recibe el nombre de Ley de Biot-Savart, que es la ley del campo magnético, equivalente a la ley de Coulomb para el campo eléctrico.
La expresión que determina la forma de H alrededor del cable conductor es:
H = 1/4p ò ò ò v{-G x (1/r3)r}dv
Imagínese a dos electrodos inmersos en un medio conductor ideal que están a potenciales diferentes medidos respecto a tierra.
El electrodo 1 se encuentra a un potencial más elevado que el electrodo 2. k es la conductividad del medio por el que fluye la corriente I. La superficie cerrada F encierra al electrodo 1 y, por lo tanto, es atravesada por la corriente I. La corriente atraviesa al medio conductor con una densidad G y así mismo a cualquier superficie que encierre al electrodo 1.
Experimentalmente puede observarse que la carga eléctrica del electrodo 1 disminuye en función del tiempo, como era de esperarse según la ley de la conservación de la carga, que reza que la carga no se crea ni se destruye.
I = - Dt Q (6)
donde Q es la carga espacial encerrada por la superficie F
Q = ò ò ò v r dv (7)
Con el teorema de Gauss se obtiene la siguiente expresión:
con las ecuaciones (6), (7) y (8) se llega a la ecuación de la continuidad
Esta ecuación comprueba la existencia de las corrientes de desplazamiento.
Forma de las ecuaciones
Las Ecuaciones de Maxwell surgen de la teoría electromagnética y son el resumen esta teoría desde un punto de vista macroscópico. Esas ecuaciones tienen la forma más general:
Y son, por tanto, un total de ocho ecuaciones escalares (tres para cada uno de los rotacionales de los campos eléctrico y magnético y una para las divergencias).
2 Parámetros presentes
Los parámetros que intervienen en la formulación de las ecuaciones de Maxwell son los siguientes:
- Campo eléctrico existente en el espacio, creado por las cargas.
- Campo dieléctrico que resume los efectos eléctricos de la materia.
- Campo magnético existente en el espacio, creado por las corrientes.
- Campo magnético que resume los efectos magnéticos de la materia.
- Densidad de cargas existentes en el espacio.
- Densidad de corriente, mide el flujo de cargas por unidad de tiempo y superfície y es igual a
.
- Permitividad eléctrica, característica de los materiales dieléctricos.
- Permeabilidad magnética, característica de los materiales paramagnéticos.
3 Significado físico
Cuando Maxwell resumió la teoría electromagnética de su época en sus ecuaciones escribió las siguientes ecuaciones:
que no es nada más que la ley de Gauss, que se reduce a la ley de Coulomb para cargas puntuales.
que no tiene nombre y expresa la inexistencia de monopolos magnéticos en la naturaleza, es decir, esta es la explicación de que al romper un imán obtengamos dos imanes, y no dos medio-imanes.
que es la expresión diferencial de la ley de Faraday.
que es la ley de Ampère. Sin embargo encontró que esta última ecuación, juntamente con la ley de Faraday conducían a un resultado que violaba el principio de conservación de la carga, con lo cual decidió modificarla para que no violase este principio dándole la forma
que ahora se conoce como ley de Ampère modificada. El término introducido recibe el nombre de corriente de desplazamiento.
Sin embargo estas ocho ecuaciones no son suficientes para resumir todo el conocimiento de la electrodinámica clásica, nos hace falta una ecuación más, esa es la expresión de la fuerza de Lorentz:
4 Soluciones de las ecuaciones
4.1 Las ecuaciones en función de dos campos
En ocasiones es conveniente expresar esas ecuaciones en función de sólo dos campos (uno eléctrico y otro magnético) relacionando los campos mediante las ecuaciones constitutivas (aquí se dan para medios isotrópicos homogéneos lineales):
con lo que podemos transformar las ecuaciones de Maxwell a la forma siguiente:
4.2 Electrostática y magnetostática
Cuando consideramos que los campos eléctrico y magnético no dependen del tiempo las ecuaciones de Maxwell se nos quedan en:
De  sacamos que el campo eléctrico se deriva del gradiente de un potencial, es decir,
sacamos que el campo eléctrico se deriva del gradiente de un potencial, es decir,  , como se desprende de la ley de Coulomb.
, como se desprende de la ley de Coulomb.
De  deducimos que el campo magnético es el rotacional de un potencial vector, es decir,
deducimos que el campo magnético es el rotacional de un potencial vector, es decir,  , obteniendo el mismo resultado que a partir de la ley de Biot-Savart.
, obteniendo el mismo resultado que a partir de la ley de Biot-Savart.
4.3 Ecuaciones de Maxwell en el vacío
Cuando estamos en el vacío podemos suponer que no existen fuentes (es decir, que  y
y  ) y las ecuaciones de Maxwell nos quedan de la forma:
) y las ecuaciones de Maxwell nos quedan de la forma:
En este caso se puede demostrar que tanto el campo  como el campo
como el campo  toman la forma de una ecuación de ondas con una velocidad
toman la forma de una ecuación de ondas con una velocidad  igual a la velocidad de la luz, de donde Maxwell extrajo la hipótesis de que la luz no eran más que ondas electromagnéticas propagándose en el vacío, hipótesis verificada esperimentalmente por Hertz algunos años después de la muerte de Maxwell.
igual a la velocidad de la luz, de donde Maxwell extrajo la hipótesis de que la luz no eran más que ondas electromagnéticas propagándose en el vacío, hipótesis verificada esperimentalmente por Hertz algunos años después de la muerte de Maxwell.
A partir de estas cuatro ecuaciones (dos de ellas vectoriales, con lo que en realidad son ocho ecuaciones escalares) se deduce la óptica electromagnética.
4.4 Caso general
El caso más general se obtiene cuando se consideran campos dependientes del tiempo y con fuentes tanto escalares como vectoriales. En ese caso resulta muy práctico obtener una expresión que nos exprese el campo electromagnético como derivación de potenciales.
De la ecuación  podemos extraer, de la teoría elemental de campos, que
podemos extraer, de la teoría elemental de campos, que  . Si sustituímos esto en la ecuación del rotacional del campo eléctrico obtenemos:
. Si sustituímos esto en la ecuación del rotacional del campo eléctrico obtenemos:
Con lo cual ya tenemos dos expresiones que nos dan la forma de los campos  y
y  en función de dos potenciales
en función de dos potenciales  y
y  . Sin embargo estos potenciales presentan cierta libertad a la hora de escogerlos lo que les hace poseer una importante característica: una simetría gauge. En efecto, si tomamos un campo escalar
. Sin embargo estos potenciales presentan cierta libertad a la hora de escogerlos lo que les hace poseer una importante característica: una simetría gauge. En efecto, si tomamos un campo escalar  y redifinimos los potenciales como
y redifinimos los potenciales como  y
y  obtenemos el mismo campo electromagnético (que al fin y al cabo es nuestro observable).
obtenemos el mismo campo electromagnético (que al fin y al cabo es nuestro observable).
5 Teoremas de conservación
De las ecuaciones de Maxwell surgen de modo natural teoremas de conservación de la carga, la energía, el momento lineal y el momento angular.
La ecuación de conservación de la carga se expresa mediante:
La ecuación de conservación de la energía toma la forma:
donde  es el vector de Poynting.
es el vector de Poynting.
La ecuación de conservación del momento lineal es:
donde  es el tensor de tensiones de Maxwell con componentes
es el tensor de tensiones de Maxwell con componentes
6 Obtención de las ecuaciones de Maxwell
Históricamente las ecuaciones de Maxwell se obtuvieron a partir de leyes empíricas que se fueron generalizando de un modo inteligente hasta llegar al conocimiento actual de la interacción electromagnética desde el punto de vista clásico. Sin embargo es posible obtener las ecuaciones de Maxwell desde un punto de vista más teórico: la teoría de la relatividad.
Podemos definir el cuadrivector potencial (se podría demostrar que éste se transforma como un cuadrivector) como:
y definir el tensor electromagnético como:
recorriendo los índices  ,
,  los índices 0 ,
los índices 0 ,  ,
,  y
y  y siendo
y siendo  .
.
Con todo esto el tensor electromagnético queda de la forma
Podemos definir también el cuadrivector corriente  (aquí se usa el convenio según el cual los índices repetidos están sumados) de forma que las ecuaciones de Maxwell se recuperan mediante la ecuación
(aquí se usa el convenio según el cual los índices repetidos están sumados) de forma que las ecuaciones de Maxwell se recuperan mediante la ecuación  .
.
7 Aplicabilidad
Las ecuaciones de Maxwell constituyen un pilar básico de la teoría electromagnética ya que por ahora se demostraron como válidas siempre. Esto es debido a que la teoría electromagnética siempre fue, sin saberlo, una teoría relativista.
De hecho, cuando se estudia desde el punto de vista cuántico estas ecuaciones sólo deben ser revisadas para tener en cuenta el carácter discreto de los fotones, pero cuando tenemos gran cantidad de ellos podemos aplicar los resultados contínuos sin ningún problema.
No fue sino hasta el año de 1820, cuando Hans Christian Ørsted descubrió que el fenómeno magnético estaba ligado al eléctrico, que se obtuvo una teoría científica para el magnetismo.7 La presencia de una corriente eléctrica, o sea, de un flujo de carga debido a una diferencia de potencial, genera una fuerza magnética que no varía en el tiempo. Si tenemos una carga q a una velocidad  , en un campo magnético
, en un campo magnético  aparecerá una fuerza magnética inducida por el movimiento en esta carga, así:
aparecerá una fuerza magnética inducida por el movimiento en esta carga, así:
 , en un campo magnético
, en un campo magnético  aparecerá una fuerza magnética inducida por el movimiento en esta carga, así:
aparecerá una fuerza magnética inducida por el movimiento en esta carga, así:
Para determinar el valor de ese campo magnético, Jean Baptiste Biot en 1820,8dedujo una relación para corrientes estacionarias, ahora conocida como ley de Biot-Savart:
Donde 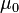 es un coeficiente de proporcionalidad conocido como permeabilidad magnética,
es un coeficiente de proporcionalidad conocido como permeabilidad magnética,  es la intensidad de corriente, el
es la intensidad de corriente, el  es el diferencial de longitud por el que circula la corriente y
es el diferencial de longitud por el que circula la corriente y  es la distancia de este elemento de longitud el punto donde se evalúa la inducción magnética. De manera más estricta,
es la distancia de este elemento de longitud el punto donde se evalúa la inducción magnética. De manera más estricta,  es la inducción magnética, dicho en otras palabras, es el flujo magnético por unidad de área. Experimentalmente se llegó a la conclusión que las líneas de fuerza de campos magnéticos eran cerradas, eliminando la posibilidad de un monopolo magnético. La relación matemática se la conoce como ley de Gauss para el campo magnético:
es la inducción magnética, dicho en otras palabras, es el flujo magnético por unidad de área. Experimentalmente se llegó a la conclusión que las líneas de fuerza de campos magnéticos eran cerradas, eliminando la posibilidad de un monopolo magnético. La relación matemática se la conoce como ley de Gauss para el campo magnético:
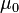 es un coeficiente de proporcionalidad conocido como permeabilidad magnética,
es un coeficiente de proporcionalidad conocido como permeabilidad magnética,  es la intensidad de corriente, el
es la intensidad de corriente, el  es el diferencial de longitud por el que circula la corriente y
es el diferencial de longitud por el que circula la corriente y  es la distancia de este elemento de longitud el punto donde se evalúa la inducción magnética. De manera más estricta,
es la distancia de este elemento de longitud el punto donde se evalúa la inducción magnética. De manera más estricta,  es la inducción magnética, dicho en otras palabras, es el flujo magnético por unidad de área. Experimentalmente se llegó a la conclusión que las líneas de fuerza de campos magnéticos eran cerradas, eliminando la posibilidad de un monopolo magnético. La relación matemática se la conoce como ley de Gauss para el campo magnético:
es la inducción magnética, dicho en otras palabras, es el flujo magnético por unidad de área. Experimentalmente se llegó a la conclusión que las líneas de fuerza de campos magnéticos eran cerradas, eliminando la posibilidad de un monopolo magnético. La relación matemática se la conoce como ley de Gauss para el campo magnético:(2)
Además en la magnetostática existe una ley comparable a la de Gauss en la electrostática, la ley de Ampère. Ésta ley nos dice que la circulación en un campo magnético es igual a la densidad de corriente que exista en una superficie cerrada:
Cabe indicar que esta ley de Gauss es una generalización de la ley de Biot-Savart. Además que las fórmulas expresadas aquí son para cargas en el vacío, para más información consúltese los artículos principales.





No hay comentarios:
Publicar un comentario