Con la tercera ecuación de Maxwell, en forma diferencial, la ausencia de fuentes del campo eléctrico
div B = 0
Se puede pensar que B = rot A(z, t), donde A(z, t) es el potencial electrodinámico vectorial libre de fuentes, es decir div A(z, t) = 0.
Sustituyendo B = rot A(z, t) en la segunda ecuación de Maxwell, la ley de Ampere, se llega a la siguiente expresión
lo que quiere decir que E + ¶/ ¶ t {A(z, t)} es el gradiente de una función escalar.
Sea j el potencial electrodinámico escalar, entonces, se puede afirmar que en una forma general
grad j = E + ¶ /¶ t {A(z, t)}
como A(r, t) es un campo que cumple con la ecuación de onda en un medio libre de fuentes, entonces, todos gradientes deben ser nulos y, por lo tanto, para que grad j = 0, debe cumplirse lo siguiente
E = -¶ /¶ t [A(z, t)]
Si se considera en z la propagación de la onda solo incidente, entonces, A(z, t) adopta la forma siguiente
A(z, t) = A1 f1( z - Vt )
Como div A(z, t) = 0, entonces
div A(z, t) = A1 grad f1( z - Vt ) + f1 div A1
donde el segundo término del segundo miembro de la igualdad es igual a cero porque A1 es un vector constante, entonces esta ecuación puede ser escrita de la manera siguiente
div A(z, t) = A1 ez ¶ ¤ ¶ z { f1( z - Vt )} = 0
lo que quiere decir que A1 es perpendicular a la dirección de propagación y, como E = -¶/¶t [A(z, t)], entonces, el campo eléctrico no tiene componente en la dirección de propagación.
Con la tercera ecuación de Maxwell, en forma diferencial, la ausencia de fuentes del campo eléctrico
div B = 0
Se puede pensar que B = rot A(z, t), donde A(z, t) es el potencial electrodinámico vectorial libre de fuentes, es decir div A(z, t) = 0.
Si se considera en z la propagación de la onda solo incidente, entonces, A(z, t) adopta la forma siguiente
A(z, t) = A1 f1( z - Vt )
Con la tercera ecuación material de Maxwell, la inducción magnética ( B = m H ), se llega a la siguiente expresión
m H = rot [A1 f1( z - Vt )] = f1( z - Vt ) rot A1 - A1 x grad f1( z - Vt )
Donde el primer término del tercer miembro de la igualdad es igual a cero ya que A1 es un vector constante. Entonces, despejado H en esta expresión se obtiene lo siguiente:
H = (1/ m )[ - A1 x ez ¶ /¶t {f1( z - Vt )}
Sustituyendo z = Vt en esta ecuación se llega a la siguiente expresión
H = ( x /m )½[ ez x E ]
Esta expresión dice que el campo magnético es ortogonal tanto al campo eléctrico como a la dirección de propagación, por lo tanto la componente del campo magnético en la dirección de propagación es cero.
Este tipo de onda, cuyas componentes del campo eléctrico y magnético en la dirección de propagación son respectivamente nulas, se conoce como onda plana.
Todas se propagan en el vacío a una velocidad constante, muy alta (300 0000 km/s) pero no infinita. Gracias a ello podemos observar la luz emitida por una estrella lejana hace tanto tiempo que quizás esa estrella haya desaparecido ya. O enterarnos de un suceso que ocurre a miles de kilómetros prácticamente en el instante de producirse.
Las ondas electromagnéticas se propagan mediante una oscilación de campos eléctricos y magnéticos. Los campos electromagnéticos al "excitar" los electrones de nuestra retina, nos comunican con el exterior y permiten que nuestro cerebro "construya" el escenario del mundo en que estamos.
Las O.E.M. son también soporte de las telecomunicaciones y el funcionamiento complejo del mundo actual.
Las cargas eléctricas al ser aceleradas originan ondas electromagnéticas
Para saber más sobre su origen y propagación pulsa aquí
Las O.E.M. son también soporte de las telecomunicaciones y el funcionamiento complejo del mundo actual.
ORIGEN Y FORMACIÓN
Las cargas eléctricas al ser aceleradas originan ondas electromagnéticas
| El campo E originado por la carga acelerada depende de la distancia a la carga, la aceleración de la carga y del seno del ángulo que forma la dirección de aceleración de la carga y al dirección al punto en que medimos el campo( sen q). Un campo electrico variable engendra un campo magnético variable y este a su vez uno electrico, de esta forma las o. e.m. se propagan en el vacio sin soporte material |
CARACTERÍSTICAS de LA RADIACIÓN E.M.
- Los campos producidos por las cargas en movimiento puden abandonar las fuentes y viajar a través del espacio ( en el vacio) creándose y recreándose mutuamente. Lo explica la tercera y cuarta ley de Maxwell.
- Las radiaciones electromagnéticas se propagan en el vacio a la velocidad de la luz "c". Y justo el valor de la velocidad de la luz se deduce de las ecuaciones de Maxwell, se halla a partir de dos constantes del medio en que se propaga para las ondas electricas y magnética .
- Los campos electricos y magnéticos son perpendiculares entre si ( y perpendiculares a la dirección de propagación) y estan en fase: alcanzan sus valores máximos y mínmos al mismo tiempo y su relación en todo momento está dada por E=c· B
- El campo eléctrico procedente de un dipolo está contenido en el plano formado por el eje del dipolo y la dirección de propagación. El enunciado anterior también se cumple si sustituimos el eje del dipolo por la dirección de movimiento de una carga acelerada
- Las ondas electromagnéticas son todas semejantes ( independientemente de como se formen) y sólo se diferencian e n su longitud de onda y frecuencia. La luz es una onda electromagnética
- Las ondas electromagnéticas transmiten energía incluso en el vacio. Lo que vibra a su paso son los campos eléctricos y magnéticos que crean a propagarse. La vibracion puede ser captada y esa energía absorberse.
- Las intensidad instantánea que posee una onda electromagnética, es decir, la energía que por unidad de tiempo atraviesa la unidad de superficie, colocada perpendicularmente a la direción de propagación es: I=c· eoE2. La intensidad media que se propaga es justo la mitad de la expresión anterior.
- La intensidad de la onda electromagnética al espandirse en el espacio disminuuye con el cuadrado de la distancia y como "I "es proporcional a E2 y por tanto a sen2Q . Por lo tanto existen direcciones preferenciales de propagación.
ORIGEN Y PROPAGACIÓN DE LAS O.E.M. |
Los campso no necesitan un medio deformable que vibre a su paso, lo único que vibra son los valores de los campos E y B en cada lugar.
Las ecuaciones de Maxwell explican esta propagación:
La carga eléctrica en movimiento crea a su alrededor un campo electromagnético, cuyas componentes E y B son perpendiculares . Sus valores en cada punto y en función del tiempo son:
E=Eosen( wt -kx)
B=Bosen( wt -kx
Las cargas eléctricas al ser aceleradas originan ondas electromagnéticas
En efecto, un campo eléctrico variable engendra un campo magnético variable que, a su vez, engendra otro eléctrico y así avanzan por el espacio.
LEYES DE MAXWELL| La variación del flujo magnético que atraviesa una superficie engendra un campo eléctrico cuya circulación a lo largo de la curva que cierra esa superficie viene dado por la fórmula aquí mostrada ( tercera ecuación de Maxweell) | |
| La variación del flujo eléctrico que atraviesa una superficie engendra un campo magnético cuya circulación a lo largo de curva que cierra dicha supericie viene dado por la fórmula aquí mostrada (cuarta ecuación de Maxwell) |
E=Eosen( wt -kx)
B=Bosen( wt -kx
Las cargas eléctricas al ser aceleradas originan ondas electromagnéticas
| Podemos elegir como modelo de formación de ondas electromagnéticas al dipolo eléctrico oscilante (dos cargas iguales y opuestas cuya separación varía armonicamente con el tiempo). Según la teoría electromagnética clásica una carga que oscila con Movimineto Armónico Simple de frecuencia "n" radia energía de la misma frecuencia. La energía que emite la transporta un campo electrico y otro magnético. Veamos como son y como se forman. |
La expresión del campo electrico (E) creado por una carga acelerada es una corrección de la deducida de la Ley de Coulomb ( E=F / q) y tiene tres términos.
El segundo introduce el efecto de la carga en el pasado. Como el campo se establece a la velocidad de la luz debemos saber donde estaba la carga y como se movía en un tiempo anterior ( el que tardo en llegar la radiación, viajando a la velocidad "c", en llegar al punto en que se mide). La carga que crea el campo, viajando a la velocidad "v", en ese momento que yo mido el campo está en otro punto distinto al que estaba cuando creo el campo E, que detectamos en ese punto de medida .
El tercer término agrega una corrección que es la variación del tiempo de retardo.
Cuando medimos E en puntos alejados de la carga oscilante el único término de la expresión que influye es el tercero.
El campo B se obtiene a partir de E
La fórmula de E refleja que el campo es función de: la acelerción de vibación del dipolo (se obtiene del tercer término); del seno del ángulo formado por la dirección de vibración y la de propagación hacia el observador; de la distancia, disminuye inversamente con la distancia ( no con el cuadrado de la distancia). La velocidad de la luz (c) aparece porque el campo no se establece instantáneamente y la carga que se mueve ejerce un efecto desde donde está y donde estuvo. Por todo lo anterior la fórmula del campo es:
cero en la dirección del eje de la antena y máximo en la dirección perpendicular a la misma.
máximo cuando "a" es máxima y varía senoidalmente como "a" ( a=- w2A·sen wt) .
E disminuye sólo inversamente proporcional a la distancia del punto en que se mide a la carga que lo crea, cuando las cargas son grandes.
La intensidad de radiación I depende del campo E radiado por una antena y es:I=c· eoE2
ESPECTRO ELECTROMAGNÉTICO |
Las ondas electromagnéticas se agrupan bajo distintas denominaciones según su frecuencia, aunque no existe un límte muy presiso para cada grupo. Además, una misma fuente de ondas electromagfnéticas puede generar al mismo tiempo ondas de varios tipos. 


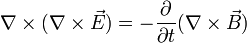
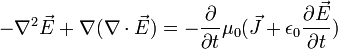
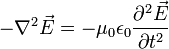

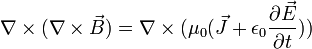

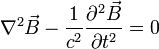
- Ondas de radio: son las utilizadas en telecomunicaciones e incluyen las ondas de radio y televisión. Su frecuencia oscila desde unos pocos hercios hasta mil millones de hercios. Se originan en la oscilación de la carga eléctrica en las antenas emisoras (dipolo radiantes).
- Microondas: Se utilizan en las comunicaciones del radar o la banda UHF ( Ultra High Frecuency) y en los hornos de las cocinas. Su frecuencia va desde los milmillones de hercios hasta casi el billon.Se producen en oscilaciones dentro de un aparato llamado magnetrón. El magnetrón es una cavidad resonante formada por dos imanes de disco en los extremos, donde los electrones emitidos por un cátodo son acelerados originado los campos electromagnéticos oscilantes de la frecuencia de microondas.
- Infrarrojos: Son emitidos por los cuerpos calientes. Los transitos energéticos implicados en rotaciones y vibraciones de las moléculas caen dentro de este rango de frecuencias. Los visores nocturnos detectan la radiación emitida por los cuerpos a una temperatura de 37 º .Sus frecuencias van desde 10 11Hz a 4·1014Hz. Nuestra piel también detecta el calor y por lo tanto las radiaciones infrarrojas.
- Luz visible: Incluye una franja estrecha de frecuencias, los humanos tenemos unos sensores para detectarla ( los ojos, retina, conos y bastones). Se originan en la aceleración de los electrones en los tránsitos energéticos entre órbitas permitidas. Entre 4·1014Hz y 8·1014Hz
- Ultravioleta: Comprende de 8·1014Hz a 1·1017Hz. Son producidas por saltos de electrones en átomos y molécualas excitados. Tiene el rango de energía que interviene en las reacciones químicas. El sol es una fuente poderosa de UVA ( rayos ultravioleta) los cuales al interaccionar con la atmósfera exterior la ionizan creando la ionosfera. Los ultravioleta puden destruir la vida y se emplean para esterilizar. Nuestra piel detecta la radiación ultravioleta y nuestro organismo se pone a fabricar melanina para protegernos de la radiación. La capa de ozono nos proteje de los UVA.
- Rayos X: Son producidos por electrones que saltan de órbitas internas en átomos pesados. Sus frecuencias van de 1'1·1017Hz a 1,1·1019Hz. Son peligrosos para la vida: una exposición prolongada produce cancer.
- Rayos gamma: comprenden frecuencias mayores de 1·1019Hz. Se origina en los procesos de estabilización en el núcleo del átomo después de emisiones radiactivas. Sus radiación es muy peligrosa para los seres vivos.
Los campos electromagnéticos se propagan por el espacio en forma de ondas, que pueden viajar a través de un medio así como en el vacío. Las ecuaciones de onda electromagnéticas son necesarias para describir la propagación de las ondas electromagnéticas, tanto en presencia de materia como en el vacío.
Ecuaciones de onda y las ecuaciones de Maxwell
Como se puede apreciar tenemos ecuaciones de onda tanto para el campo eléctrico  como para el campo magnético
como para el campo magnético  , que son obtenidas a partir de las ecuaciones de Maxwell teniendo que:
, que son obtenidas a partir de las ecuaciones de Maxwell teniendo que:
 como para el campo magnético
como para el campo magnético  , que son obtenidas a partir de las ecuaciones de Maxwell teniendo que:
, que son obtenidas a partir de las ecuaciones de Maxwell teniendo que:

Para obtener las ecuaciones es necesario aplicar el operador rotacional a ambas.
Ecuación de onda para E
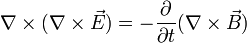
Sustituyendo 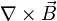 y aplicando identidad de rotacional tenemos:
y aplicando identidad de rotacional tenemos:
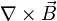 y aplicando identidad de rotacional tenemos:
y aplicando identidad de rotacional tenemos: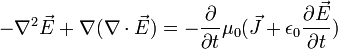
Ahora bien, sabemos que la segunda parte del lado izquierdo es cero y 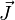 es cero en el vacío, quedándonos solo
es cero en el vacío, quedándonos solo
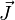 es cero en el vacío, quedándonos solo
es cero en el vacío, quedándonos solo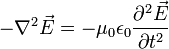
Ahora, igualando a cero y sabiendo que  , siendo c la velocidad de la luz, tenemos la ecuación de onda para
, siendo c la velocidad de la luz, tenemos la ecuación de onda para  :
:
 , siendo c la velocidad de la luz, tenemos la ecuación de onda para
, siendo c la velocidad de la luz, tenemos la ecuación de onda para  :
:
Ecuación de onda para B
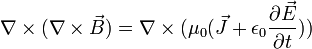
Aplicando las mismas identidades que con  y sabiendo que
y sabiendo que 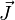 , también es cero, nos queda:
, también es cero, nos queda:
 y sabiendo que
y sabiendo que 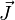 , también es cero, nos queda:
, también es cero, nos queda:
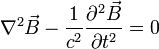
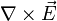 e igualando a cero, tenemos la
e igualando a cero, tenemos la
No hay comentarios:
Publicar un comentario