Impulso y cantidad de movimiento
Cantidad de movimiento
Aquellas magnitudes que se conservan constantes durante algún proceso de interacción, son muy útiles para la determinación de las cantidades físicas involucradas en el proceso antes y después de realizado, como es el caso de la ley de la conservación de la energía o el teorema trabajo-energía. Ahora identificaremos otra cantidad que se conserva en los sistemas aislados: la cantidad de movimiento. Como el nombre lo indica este concepto es otra magnitud derivada del movimiento de los cuerpos y está relacionado con la segunda ley de Newton.La segunda ley de Newton (F = ma) mantiene su certeza aun en el caso de sistemas donde la masa cambie, se agregue o quite masa del sistema. Si consideramos ahora que en un proceso físico donde se aplique una fuerza constante a un cuerpo, la masa del cuerpo cambie una cantidad finita fija esta ley se puede expresar como:
| (ecuación 1) |
Agrupando los términos de otra forma por conveniencia podemos llega a:
| (ecuación 2) |
Figura 1 |
p = mv (ecuación 3)
La cantidad de movimiento es un vector cuya dirección es la misma que la de la velocidad y cuya unidad, como se puede deducir de la ecuación 3, es kg·m/seg.
Sustituyendo en la ecuación 2 el factor (mv) por el nuevo concepto de cantidad de movimiento, tendremos una expresión de la segunda ley de Newton en términos de cantidad de movimiento:
| (ecuación 4) |
Esta expresión, en palabras, significa que cuando a un cuerpo se le aplica una fuerza su cantidad de movimiento cambia con respecto al tiempo, y es evidente, ya que la fuerza provoca una aceleración, por lo tanto un cambio de velocidad lo que según la definición, p = mv, produce también un cambio en la cantidad de movimiento del cuerpo.
La importancia de la cantidad de movimiento no solo radica en que es una presentación de la segunda ley de Newton en una nueva forma, si no, también, porque juega un rol central en una importante ley de conservación.
Conservación de la cantidad de movimiento.
Consideremos la interacción entre dos cuerpos 1 y 2 de la figura 1. Aquí hemos considerado los cuerpos como puntuales, pero el procedimiento es utilizable para cuerpos reales utilizando su centro de masa. Decir que dos cuerpos interactúan es lo mismo que decir que uno ejerce una fuerza sobre el otro, y según la tercera ley de Newton, de la acción y la reacción, los cuerpos reciben mutuamente una fuerza de igual magnitud y de sentido contrario.Cuando interactúan las dos partículas lo pueden hacer de varias formas, pueden estar en contacto (figura 1a), como cuando chocan dos bolas, lo pueden hacer a distancia (figura 1b), que es el caso de la fuerza de atracción de la Tierra y la luna, o también a través de un elemento elástico (figura 1c) como un resorte. Nombremos como F12 a la fuerza que ejerce el cuerpo 1 sobre el cuerpo 2 y F21 a la que hace el cuerpo 2 sobre el 1. La tercera ley de Newton establece que:
F12 = - F21 (ecuación 5)
El signo menos en la parte derecha de la ecuación 5 significa que las fuerzas tienen sentido contrario.
Si expresamos las fuerzas en términos de la cantidad de movimiento:
| (ecuación 6) |
| (ecuación 7) |
Ahora la expresión 5 toma la forma:
| (ecuación 8) |
O bien:
| (ecuación 9) |
La ecuación 9 dice que la suma de la tasa de cambio con respecto al tiempo, de las cantidades de movimiento de dos cuerpos que interactúan es cero, lo que significa que:
p1 + p2 = una constante (expresión 1)
La expresión 1 es la presentación matemática de un principio físico importante:
La suma de las cantidades de movimiento de un sistema aislado de dos cuerpos que ejercen fuerzas uno al otro es una constante, no importa la forma en que las fuerzas se ejerzan.


La cantidad de movimiento sirve, por ejemplo, para diferenciar dos cuerpos que tengan la misma velocidad, pero distinta masa. El de mayor masa, a la misma velocidad, tendrá mayor cantidad de movimiento.

m = Masa
v = Velocidad (en forma vectorial)
p = Vector cantidad de movimiento

Dado que el impulso es igual a la fuerza por el tiempo, una fuerza aplicada durante un tiempo provoca una determinada variación en la cantidad de movimiento, independientemente de su masa:





b) Velocidades de igual dirección y sentido contrario.




Esta regla es una profunda y general ley de la naturaleza con la que se pueden resolver muchos problemas.
Matemáticamente puede expresarse como:
Donde Fp es la magnitud promedio de la fuerza actuante y Δt = t2 - t1 , el lapso de tiempo en el actúa la fuerza. No es difícil determinar que las unidades del impulso son las mismas que para la cantidad de movimiento, kg·m/seg.
El concepto de impulso encuentra su mayor aplicación en el caso de las llamadas fuerzas impulsivas, que son aquellas que actúan sobre un cuerpo durante un breve período de tiempo, como en el caso de los choques, las explosiones y otros fenómenos de esa naturaleza.
Impulso
El impulso y la cantidad de movimiento son conceptos muy íntimamente relacionados, tanto, que en ocasiones se pueden confundir, pero son aspectos diferenciados de la acción de fuerzas sobre los cuerpos. Habíamos visto arriba que la cantidad de movimiento era p = mv lo que implica que cualquier cuerpo de masa m que se mueve a cierta velocidad tiene una cierta cantidad de movimiento, si consideramos ahora que sobre el cuerpo actúa una fuerza por cierto tiempo, esta fuerza modificará la cantidad de movimiento del cuerpo, debido a que necesariamente cambiará su velocidad, en esta situación es que entra en juego el concepto de impulso, el que podía definirse como:
El impulso es el cambio en la cantidad de movimiento de un cuerpo que produce una fuerza que actúa durante un cierto tiempo.
Matemáticamente puede expresarse como:
I = FpΔt (ecuación 10)
Donde Fp es la magnitud promedio de la fuerza actuante y Δt = t2 - t1 , el lapso de tiempo en el actúa la fuerza. No es difícil determinar que las unidades del impulso son las mismas que para la cantidad de movimiento, kg·m/seg.
El concepto de impulso encuentra su mayor aplicación en el caso de las llamadas fuerzas impulsivas, que son aquellas que actúan sobre un cuerpo durante un breve período de tiempo, como en el caso de los choques, las explosiones y otros fenómenos de esa naturaleza.
Impulso y cantidad de movimiento
Impulso
El impulso es el producto entre una fuerza y el tiempo durante el cual está aplicada. Es unamagnitud vectorial. El módulo del impulso se representa como el área bajo la curva de la fuerza en el tiempo, por lo tanto si la fuerza es constante el impulso se calcula multiplicando la F por Δt, mientras que si no lo es se calcula integrando la fuerza entre los instantes de tiempo entre los que se quiera conocer el impulso.Cantidad de Movimiento
La cantidad de movimiento es el producto de la velocidad por la masa. La velocidad es un vector mientras que la masa es un escalar. Como resultado obtenemos un vector con la misma dirección y sentido que la velocidad.La cantidad de movimiento sirve, por ejemplo, para diferenciar dos cuerpos que tengan la misma velocidad, pero distinta masa. El de mayor masa, a la misma velocidad, tendrá mayor cantidad de movimiento.
m = Masa
v = Velocidad (en forma vectorial)
p = Vector cantidad de movimiento
Relación entre Impulso y Cantidad de Movimiento
El impulso aplicado a un cuerpo es igual a la variación de la cantidad de movimiento, por lo cual el impulso también puede calcularse como:Dado que el impulso es igual a la fuerza por el tiempo, una fuerza aplicada durante un tiempo provoca una determinada variación en la cantidad de movimiento, independientemente de su masa:
IMPULSO Y CANTIDAD DE MOVIMIENTO
Según el principio de masa, si a ésta se le aplica una fuerza F adquiere una aceleración a:
F = m.a
Siendo:
F: fuerza [F] = N (Newton)
a: aceleración [a] = m/s²
m: masa [m] = kg
Multiplicando ambos miembros por el tiempo T en que se aplica la fuerza F:
F.t = m.a.t
Como:
a.t = v
siendo:
v: velocidad [v] = m/s
t: tiempo [t] = s
Tenemos:
F.t = m.v
Al término F.t se lo denomina impulso de la fuerza y al término m.v se lo denomina cantidad de movimiento, entonces, para el primero:
I = F.t
siendo:
I: impulso [I] = kg.m/s
para el segundo:
p = m.v
siendo:
p: cantidad de movimiento [p] = kg.m/s
Para deducir las unidades, tenemos:
F.t = m.v
N.s = kg.m/s N = kg.m/s²
kg.m/s².s = kg.m/s
luego:
[I] = [p] = kg.m/s = N.s
El impulso de la fuerza aplicada es igual a la cantidad de movimiento que provoca, o dicho de otro modo, el incremento de la cantidad de movimiento de cualquier cuerpo es igual al impulso de la fuerza que se ejerce sobre él.
Unidades en los distintos sistemas
c.g.s.
|
S.I.
|
Técnico
| |
Cantidad de movimiento
Impulso
|
g.m/s
din.s
|
kg.m/s
N.s
|
kgf.s
kgf.s
|
El impulso y la cantidad de movimiento son magnitudes vectoriales.
Conservación de la cantidad de movimiento
Si con un cuerpo de masa m1 y velocidad v1 se aplica una fuerza a otro cuerpo de masa m2 y velocidad v2, como por ejemplo, en un saque de tenis, en ese instante es aplicable el principio de acción y reacción y tenemos que:
m1.v1 = m2.v2
es decir la masa de la raqueta por su velocidad, en el momento del choque, debe ser igual a la masa de la pelota de tenis por la velocidad que adquiere.
Enunciando la Ley de conservación de la cantidad de movimiento dice:
En cualquier sistema o grupo de cuerpos que interactúen, la cantidad de movimiento total, antes de las acciones, es igual a la cantidad de movimiento total luego de las acciones.
Σm.v = 0
mi.vi = mf.vf
ΔP = Δp1 + Δp2
Choque
Se produce choque entre dos cuerpos cuando uno de ellos encuentra en su trayectoria a otro y produciéndose contacto físico.
Al producirse el choque también se producen deformaciones en ambos cuerpos, éstas pueden desaparecer de inmediato o perdurar. Si las deformaciones desaparecen rápidamente significa que se ha producido un choque elástico, por el contrario, si permanecen se ha producido un choque inelástico o plástico.
En ambos casos ocurre una variación de la energía cinética que se transformará en calor que disiparán los cuerpos.
1) Choque plástico o inelástico
a) Velocidades de igual dirección y sentido
Supongamos un cuerpo 1 de masa m1 y velocidad v1 que se dirige a hacia el cuerpo 2 de masa m2 y velocidad v2, siendo ambas velocidades de igual dirección y sentido. Sobre cada cuerpo actuó en el momento del choque, el impulso que le provocó el otro cuerpo, entonces hay dos acciones de igual intensidad y sentido contrario, en consecuencia ambas cantidades de movimiento serán iguales y de sentido contrario. Luego del choque ambos cuerpos continúan juntos con una velocidad final común a ambos.
La velocidad final será:
m1.v1i + m2.v2i = m1.v1f + m2.v2f
como v1f y v2f son iguales porque ambos cuerpos siguen juntos:
v1f = v2f = vf
m1.v1i + m2.v2i = (m1 + m2).vf
vf = (m1.v1i + m2.v2i)/(m1 + m2)
b) Velocidades de igual dirección y sentido contrario.
En este caso los cuerpos poseían velocidades de igual dirección pero de sentido contrario antes del choque, como en el caso anterior luego del impacto continúan juntos, con una velocidad final que estará dada por la diferencia de las cantidades de movimiento. La velocidad final será:
m1.v1i - m2.v2i = m1.v1f + m2.v2f
igualmente:
v1f = v2f = vf
m1.v1i - m2.v2i = (m1 + m2).vf
vf = (m1.v1i - m2.v2i)/(m1 + m2)
La velocidad final mantendrá la misma dirección pero tendrá el sentido de la velocidad del cuerpo que antes del choque tenga más cantidad de movimiento.
2) Choque elástico
a) Velocidades de igual sentido
Durante el choque cada cuerpo recibe una cantidad de movimiento que es igual a la velocidad perdida por el otro. Al recuperar su forma inicial, cada uno pierde o gana respectivamente, la cantidad de movimiento ganada o perdida en el momento del choque, la velocidad final de cada uno será:
v1f = (v2f + v2i).m2/m1 + v1i
ó:
v1f = v2f + v2i - v1i
b) Velocidades de distinto sentido
En este caso los cuerpos literalmente rebotan, y la velocidad final de cada uno será:
v1f = (v2f - v2i).m2/m1 + v1i
El principio de conservación del impulso es el mismo que el de conservación de la cantidad de movimiento.
Cabe aclarar que en la práctica podemos aplicar el principio de conservación de la cantidad de movimiento durante los choques, siempre que el tiempo que dura el impacto sea muy pequeño.
impulso a la magnitud física, denotada usualmente como I, definida como la variación en el momento lineal que experimenta un objeto físico en un sistema cerrado. El término difiere de lo que cotidianamente conocemos como impulso y fue acuñado por Isaac Newton en su segunda ley, donde lo llamó vis motrix, refiriéndose a una especie de fuerza del movimiento.
Definición formal
La Segunda ley de Newton se encarga de cuantificar el concepto de fuerza. Nos dice que la fuerza neta aplicada sobre un cuerpo es proporcional a la aceleración que adquiere dicho cuerpo . Las constante de proporcionalidad es la masa del cuerpo , de manera que podemos expresar la relación de la siguiente manera :
Definición más simple
El concepto de impulso se puede introducir mucho antes del conocimiento sobre el cálculo diferencial e integral con algunas consideraciones. Si consideramos unamasa que no varía en el tiempo sujeta a la acción de una fuerza también constante, la cantidad de movimiento se puede tomar como el simple producto entre lavelocidad (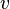 ) y la masa (
) y la masa ( ). Según la segunda ley de Newton, si a una masa
). Según la segunda ley de Newton, si a una masa  se le aplica una fuerza
se le aplica una fuerza 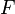 aquélla adquiere una aceleración
aquélla adquiere una aceleración  , de acuerdo con la expresión:
, de acuerdo con la expresión:
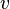 ) y la masa (
) y la masa ( ). Según la segunda ley de Newton, si a una masa
). Según la segunda ley de Newton, si a una masa  se le aplica una fuerza
se le aplica una fuerza 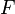 aquélla adquiere una aceleración
aquélla adquiere una aceleración  , de acuerdo con la expresión:
, de acuerdo con la expresión:
multiplicando ambos miembros por el tiempo 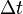 en que se aplica la fuerza designada:
en que se aplica la fuerza designada:
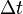 en que se aplica la fuerza designada:
en que se aplica la fuerza designada:
Como  , tenemos:
, tenemos:
 , tenemos:
, tenemos:
y finalmente:
que es equivalente a () cuando la fuerza no depende del tiempo.
Unidades
Un impulso cambia el momento lineal de un objeto, y tiene las mismas unidades y dimensiones que el momento lineal. Las unidades del impulso en el Sistema Internacional son kg·m/s.
Para deducir las unidades podemos utilizar la definición más simple, donde tenemos:
considerando que ![\left [ N \right ] = \left [ {kg} \frac{m}{s^2} \right ]](https://upload.wikimedia.org/math/8/1/5/815d94802f409501f94ade165b19021a.png) , y sustituyendo, resulta
, y sustituyendo, resulta
![\left [ N \right ] = \left [ {kg} \frac{m}{s^2} \right ]](https://upload.wikimedia.org/math/8/1/5/815d94802f409501f94ade165b19021a.png) , y sustituyendo, resulta
, y sustituyendo, resulta
y efectivamente,
con lo que hemos comprobado que ![\left [ I \right ] = \left [\Delta p \right ]](https://upload.wikimedia.org/math/8/b/d/8bd776b5dac17b47af5f2573972806ce.png) , por lo que el impulso de la fuerza aplicada es igual a la cantidad de movimiento que provoca, o dicho de otro modo, el incremento de la cantidad de movimiento de cualquier cuerpo es igual al impulso de la fuerza que se ejerce sobre él.
, por lo que el impulso de la fuerza aplicada es igual a la cantidad de movimiento que provoca, o dicho de otro modo, el incremento de la cantidad de movimiento de cualquier cuerpo es igual al impulso de la fuerza que se ejerce sobre él.
![\left [ I \right ] = \left [\Delta p \right ]](https://upload.wikimedia.org/math/8/b/d/8bd776b5dac17b47af5f2573972806ce.png) , por lo que el impulso de la fuerza aplicada es igual a la cantidad de movimiento que provoca, o dicho de otro modo, el incremento de la cantidad de movimiento de cualquier cuerpo es igual al impulso de la fuerza que se ejerce sobre él.
, por lo que el impulso de la fuerza aplicada es igual a la cantidad de movimiento que provoca, o dicho de otro modo, el incremento de la cantidad de movimiento de cualquier cuerpo es igual al impulso de la fuerza que se ejerce sobre él.Conservación del momento lineal
Como hemos visto, la variación en la cantidad del movimiento y el impulso van estrechamente ligados. La conservación de la cantidad de movimiento lineal es una de las cantidades físicas que en un sistema cerrado aparecen inalterables. Así, si sobre un sistema no se ejerce fuerza neta alguna, el momento lineal total del sistema no puede variar. Y para nuestro caso: para hacer variar la cantidad de movimiento de un cuerpo es necesario aplicarle un impulso producto de una fuerza.2
Choques
Los choques son interacciones de dos o más cuerpos en el que existe contacto entre ellos durante un tiempo tanto determinado como indeterminado. Existen distintos tipos de choque, los choques elásticos, inelásticos y perfectamente inelásticos. Todos estos choques tienen la característica de conservar su momentum o cantidad de movimiento, pero no así su energía mecánica, que en la mayoría de los casos solo se considera la energía cinética. Los choques elásticos mantienen el momentum inicial del sistema al igual que la energía cinética total del sistema. Dentro de este tipo de choque es importante mencionar un caso importante, que es el choque de dos cuerpos de igual masa y uno de ellos inicialmente en reposo. Al impactar se transferirá la energía desde el cuerpo en movimiento hacia el que no se está moviendo, quedando el cuerpo inicialmente en movimiento en reposo, mientras que el otro seguirá en movimiento, el mismo que seguía el primer cuerpo, un ejemplo de este es el juego de pool o billar. Mientras dura el choque cabe señalar que en el contacto de ambos cuerpos la energía se almacena en una deformación mínima y no permanente.
Choque elástico
En física, en el caso ideal, una colisión perfectamente elástica es un choque entre dos o más cuerpos que no sufren deformaciones permanentes debido al impacto. En una colisión perfectamente elástica se conservan tanto el momento lineal como la energía cinética del sistema. Claro está que durante una colisión, aunque sean de dos sólidos, no se puede considerar perfectamente elástico ya que siempre hay una deformación.
Las colisiones en las que la energía no se conserva producen deformaciones permanentes de los cuerpos y se denominan colisiones inelásticas.
Colisiones elásticas son aquellas en las cuales no hay intercambio de masa entre los cuerpos que colisionan, sin embargo, hay conservación neta de energía cinética.
Choque perfectamente inelástico
En un choque inelástico (o choque plástico) los cuerpos presentan deformaciones luego de su separación, esto es una consecuencia del trabajo realizado. En el caso ideal de un choque perfectamente inelástico, los objetos en colisión permanecen pegados entre sí. El marco de referencia del centro de masas permite presentar una definición más precisa. En los choques inelásticos la energía cinética no se conserva, ya que parte de ella es "usada" para deformar el cuerpo.
Es por esto que se puede decir que en el choque inelástico la energía se ve reducida debido a la incapacidad de regresar a su estado original los cuerpos.
De tal manera que en el choque inelástico habrá transformación de energía mientras en contraste, el choque elástico la mantendrá constante.
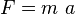



![\left [ N\,s \right ]= \left [ kg \frac {m}{s} \right ]](https://upload.wikimedia.org/math/1/e/0/1e042ac0757c967723a7c62bd220c29d.png)
![\left [kg \frac {m}{s^2}\,s \right] = \left [ kg \frac {m}{s} \right ]](https://upload.wikimedia.org/math/5/6/a/56a602f757d17bd69307bc2d4e37b28e.png)
![\left [ kg \frac {m}{s} \right ] = \left [ kg \frac {m}{s} \right ]](https://upload.wikimedia.org/math/6/3/2/63269cae07e0df62e43d178ad6d51c09.png)
No hay comentarios:
Publicar un comentario