Energía potencial eléctrica
energía potencial, o de posición, en tal objeto era posible debido a la naturaleza conservativa de la fuerza de la gravedad.
La acción a distancia de las fuerzas gravitacionales sugiere que de alguna manera debe llegar la fuerza creada por uno de los cuerpos al otro, y una forma elegante de resolver este asunto fue considerar que los cuerpos influyen en el espacio que los rodea y a esa infuencia se le llamócampo, que estaba presente aunque el otro cuerpo existiera o no, dando origen al concepto de campo gravitacional.
Del mismo modo, la fuerza de interacción entre dos cuerpos con carga eléctrica sugirió la presencia de un campo, ahora campo eléctrico, que rodeaba a los cuerpos cargados y que estaba presente aunque solo uno de los cuerpos existiera. La experimentación condujo a determinar que existe una gran similitud entre la fuerza de interacción gravitacional entre dos cuerpos con masa y la fuerza de interacción eléctrica entre dos cuerpos con carga eléctrica. Ambas fuerzas son inversamente proporcionales al cuadrado de la distancia entre los cuerpos y ambas son conservativas, con la diferencia de que siempre la fuerza de gravedad es de atracción mientras que la fuerza eléctrica puede ser de atracción o de repulsión de acuerdo al signo de las cargas involucradas.
La fuerza de atracción gravitacional entre dos cuerpos, uno de masa m y otro de masa m0 separados una distancia r reponde a la expresión:
Donde G es la constante de la gravitación universal.
Por su parte, la fuerza eléctrica sobre una carga q0 debido a una carga q separadas una distancia r es:
Donde ε0 es una constante llamada permitividad.
Ambas expresiones tienen un sorprendente parecido, en la primera el producto de las masas, afectado por la constante G, se divide por la distancia de separación entre las masas al cuadrado; en la segunda el producto de las cargas, afectado por la constante 4πε0, se divide también por la distancia entre las cargas al cuadrado.
¿En cual situación un sistema formado por dos o más masas, o por dos o más cargas, no tiene energía potencial?, el simple razonamiento nos dice que esto se da cuando la distancia entre las masas o las cargas es infinita (la fuerza en las expresiones 2 y 3 es cero). Del razonamiento de desprende que la energía potencial se adquiere cuando se produce un desplazamiento de las masas o las cargas y se colocan a una distancia finita. Pero para colocar las masas o las cargas en la nueva posición se ha tenido que realizar trabajo sobre ellas y este trabajo es el producto de la fuerza F (de las expresiones 2 y 3 según el caso) por el desplazamiento realizado.
Según la ley de la conservación de la energía el trabajo realizado solo pudo convertirse en energía potencial una vez que los cuerpos están fijos en la posición finita alcanzada. De esta situación podemos enunciar que la energía potencial eléctrica de un sitema de cargas es equivalente a la cantidad de trabajo hecho sobre las cargas eléctricas para traerlas desde el infinito hasta la posición considerada, lo que implica, de hecho, que la energia potencial es siempre una energía de posición como ya se ha dicho antes.
Note que en un sistema real de dos cargas separadas una distancia r siempre habrá una cierta cantidad de energía potencial en función de r y la magnitud de esta energía responde a la expresión que brindaremos sin demostración:
Note que de la ecuación 3 se desprende que la energía potencial eléctrica (al igual que la gravitacional) es independiente del camino seguido por las cargas durante el desplazamiento y solo depnde de la distancia r entre ellas.
Echemos un vistazo ahora al significado físico de la ecuación 3 utilizando un sistema de dos cargas que se mueven entre dos distancias, una distancia r1 y otra distancia r2 como se muestra en la figura 1. Suponga primero que las cargas se acercan. Si las cargas se repelen (el producto qq0 es positivo ya que se multiplican dos cargas del mismo signo) el cambio en la energía potencial es positiva, y se ha tenido que realizar trabajo sobre el sistema para vencer la fuerza de repulsión. Esto es como si se desplazara una roca cuesta arriba en una montaña. Si las cargas se atraen (qq0 es negativo) y el sistema pierde energía potencial cuando las cargas se acercan. Esto es como si se desplazara una roca cuesta abajo en una montaña. Como en cualquier energía potencial, la energía potencial eléctrica puede convertirse a energía cinética. Si no actúa ninguna fuerza adicional, entonces las cargas del mismo signo bajan la velocidad o la energía cinética a medida que se acercan. Similarmente las cargas de signo contrario aumentan la velocidad o ganan energía cinética cuando se acercan. El mismo análisis se puede hacer para el caso de que las cargas se separen. Las cargas que se repelen pierden energía potencial eléctrica, o ganan energía cinética a medida que se juntan si no hay otras fuerzas. Las cargas opuestas (que se atraen) ganan energía potencial eléctrica a medida que se separan y pierden energía cinética en ausencia de otras fuerzas.
La acción a distancia de las fuerzas gravitacionales sugiere que de alguna manera debe llegar la fuerza creada por uno de los cuerpos al otro, y una forma elegante de resolver este asunto fue considerar que los cuerpos influyen en el espacio que los rodea y a esa infuencia se le llamócampo, que estaba presente aunque el otro cuerpo existiera o no, dando origen al concepto de campo gravitacional.
Del mismo modo, la fuerza de interacción entre dos cuerpos con carga eléctrica sugirió la presencia de un campo, ahora campo eléctrico, que rodeaba a los cuerpos cargados y que estaba presente aunque solo uno de los cuerpos existiera. La experimentación condujo a determinar que existe una gran similitud entre la fuerza de interacción gravitacional entre dos cuerpos con masa y la fuerza de interacción eléctrica entre dos cuerpos con carga eléctrica. Ambas fuerzas son inversamente proporcionales al cuadrado de la distancia entre los cuerpos y ambas son conservativas, con la diferencia de que siempre la fuerza de gravedad es de atracción mientras que la fuerza eléctrica puede ser de atracción o de repulsión de acuerdo al signo de las cargas involucradas.
La fuerza de atracción gravitacional entre dos cuerpos, uno de masa m y otro de masa m0 separados una distancia r reponde a la expresión:
| (ecuación 1) |
Por su parte, la fuerza eléctrica sobre una carga q0 debido a una carga q separadas una distancia r es:
| (ecuación 2) |
¿En cual situación un sistema formado por dos o más masas, o por dos o más cargas, no tiene energía potencial?, el simple razonamiento nos dice que esto se da cuando la distancia entre las masas o las cargas es infinita (la fuerza en las expresiones 2 y 3 es cero). Del razonamiento de desprende que la energía potencial se adquiere cuando se produce un desplazamiento de las masas o las cargas y se colocan a una distancia finita. Pero para colocar las masas o las cargas en la nueva posición se ha tenido que realizar trabajo sobre ellas y este trabajo es el producto de la fuerza F (de las expresiones 2 y 3 según el caso) por el desplazamiento realizado.
Según la ley de la conservación de la energía el trabajo realizado solo pudo convertirse en energía potencial una vez que los cuerpos están fijos en la posición finita alcanzada. De esta situación podemos enunciar que la energía potencial eléctrica de un sitema de cargas es equivalente a la cantidad de trabajo hecho sobre las cargas eléctricas para traerlas desde el infinito hasta la posición considerada, lo que implica, de hecho, que la energia potencial es siempre una energía de posición como ya se ha dicho antes.
Note que en un sistema real de dos cargas separadas una distancia r siempre habrá una cierta cantidad de energía potencial en función de r y la magnitud de esta energía responde a la expresión que brindaremos sin demostración:
| (ecuación 3) |
Figura1. Cargas que se mueven entre r1 y r2 |
energía potencial gravitatoria estudiamos que un cuerpo que se encuentra a determinada altura de la superficie de la Tierra adquiere una determinada cantidad de energía potencial provocada por la acción de la fuerza gravitatoria. De igual forma, un cuerpo cargado que sufre la acción de unafuerza eléctrica adquiere energía potencial electrostática.
La energía potencial eléctrica que posee una carga puntual q1 en presencia de otra carga puntual q2 que se encuentran separadas cierta distancia es
donde:
- Ep es la energía potencial eléctrica. En el S.I. se mide en Julios (J).
- q1 y q2 son los valores de las dos cargas puntuales. En el S.I. se miden en Culombios (C).
- r es el valor de la distancia que las separa. En el S.I. se mide en metros (m).
- K es la constante de la ley de Coulomb. Para el vacío su valor es aproximadamente 9·109 N·m2/C2utilizando unidades en el S.I.
Date cuenta que la energía potencial eléctrica es:
- positiva si las cargas poseen el mismo signo y negativa si tienen signos distintos.
- nula cuando la distancia de separación es infinita.
Relación entre el trabajo eléctrico y la energía potencial eléctrica
Como ocurre con todas las fuerzas conservativas, existe una relación entre el trabajo eléctrico y la energía potencial eléctrica. En concreto, el trabajo que realiza una fuerza eléctrica para desplazar una carga desde un punto A hasta otro B puede expresarse de la siguiente forma:
o lo que es lo mismo:
Fuerzas Externas contrarias a la Fuerza Eléctrica
Como ya hablamos en el apartado de trabajo eléctrico, este es el trabajo que realizan las fuerzas eléctricas y no debemos confundirlo con el trabajo que puede realizar una fuerza externa en contra de las fuerzas eléctricas para intentar aproximar dos cuerpos cargados con el mismo signo (que apriori intentarán separarse) o alejar dos cuerpos cargados con distinto signo (que apriori intentarán unirse). El trabajo que realiza dicha fuerza (Wf) se relaciona con el trabajo eléctrico (We) y la energía potencial eléctrica de la siguiente forma :
A continuación, vamos a estudiar que esta relación se cumple en los dos casos comentados anteriormente.
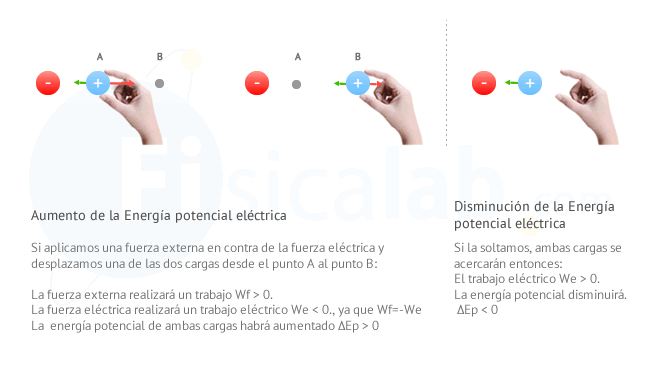
Cargas con distinto signo
Imagina dos cargas fijas, una positiva y otra negativa. En principio, dado que se trata de cargas con distinto signo en cada una de ellas aparecerá una fuerza de atracción hacia la otra. Imagina nuevamente que una de ellas se encuentra en un punto A y que podemos cogerla con la mano y situarla hasta un punto B más alejado. Al hacer esto:
- Si aplicas la definiciónde trabajo, dado que el desplazamiento se produce en la dirección y sentido de la fuerza externa, el trabajo que realiza esta fuerza (Wf) será positivo (Wf>0).
- Como el desplazamiento se produce en sentido contrario a la fuerza eléctrica, el trabajo eléctrico será negativo (We<0 span="">
- Si aplicas la definición de energía potencial eléctrica, podrás comprobar que la energía en B es mayor que en A, por tanto (ΔEp>0).
En resumidas cuentas, el trabajo que realiza la fuerza externa al alejarlas, hace que las cargas adquieran energía potencial. Si ahora la soltamos, la fuerza eléctrica se encargará de acercarlas realizando un trabajo que consumirá parte o toda la energía potencial que poseen.
Cargas del mismo signo
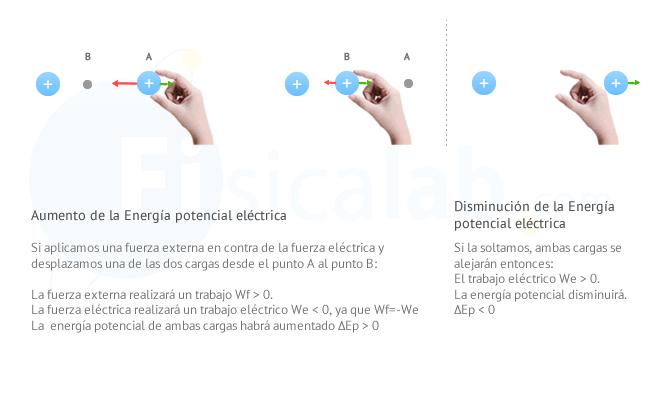
Ahora, imagina dos cargas fijas del mismo signo (positiva o negativa). En principio, dado que se trata de cargas con signos iguales en cada una de ellas aparecerá una fuerza de repulsión en contra de la otra. Imagina nuevamente que una de ellas se encuentra en un punto A y que podemos cogerla con la mano y situarla hasta un punto B más cercano. Al hacer esto, como en el caso anterior:
- Si aplicas la definiciónde trabajo, dado que el desplazamiento se produce en la dirección y sentido de la fuerza externa, el trabajo que realiza esta fuerza (Wf) será positivo (Wf>0).
- Como el desplazamiento se produce en sentido contrario a la fuerza eléctrica, el trabajo eléctrico será negativo (We<0 span="">.
- Si aplicas la definición de energía potencial eléctrica, podrás comprobar que la energía en B es mayor que en A, por tanto (ΔEp>0).
El trabajo que realiza la fuerza externa al acercarlas, hace que las cargas adquieran energía potencial. Si ahora la soltamos, la fuerza eléctrica se encargará de alejarlas realizando un trabajo que consumirá parte o toda la energía potencial que poseen.
Fíjate que tal y como indicamos en la fórmula inicial, cuando se aplica la fuerza externa, el signo del trabajo delcampo eléctrico es exactamente el contrario al del trabajo realizado por la fuerza eléctrica y al de la diferencia de energía potencial.
La Energía Potencial Eléctrica y Potencial Eléctrico
La energía potencial eléctrica y potencial eléctrico
Nos enteramos de que en el capítulo de energía de trabajo de energía, los objetos tienen energía potencial debido a sus posiciones. En este caso de carga en un campo eléctrico también la energía potencial debido a sus posiciones. Puesto que hay una fuerza sobre la carga y lo hace en contra de que esta fuerza se puede decir que se debe tener la energía para hacer el trabajo. En otras palabras, podemos decir que la energía necesaria aumentar la distancia entre dos cargas hasta el infinito, o viceversa. Energía potencial eléctrica es una magnitud escalar y Joule es la unidad de la misma. Nosotros utilizamos la siguiente fórmula para encontrar la magnitud de la EP;
Nos enteramos de que en el capítulo de energía de trabajo de energía, los objetos tienen energía potencial debido a sus posiciones. En este caso de carga en un campo eléctrico también la energía potencial debido a sus posiciones. Puesto que hay una fuerza sobre la carga y lo hace en contra de que esta fuerza se puede decir que se debe tener la energía para hacer el trabajo. En otras palabras, podemos decir que la energía necesaria aumentar la distancia entre dos cargas hasta el infinito, o viceversa. Energía potencial eléctrica es una magnitud escalar y Joule es la unidad de la misma. Nosotros utilizamos la siguiente fórmula para encontrar la magnitud de la EP;
¡Ten cuidado!
En esta fórmula si las cargas tienen signo opuesto entonces, Ep pasa a ser negativo, si son el mismo tipo de carga luego, Ep es positiva.
Si Ep es positivo, entonces, la energía potencial eléctrica es inversamente proporcional a la distancia d.
Si Ep es negativa, entonces, la energía potencial eléctrica es directamente proporcional a la distancia d.
En esta fórmula si las cargas tienen signo opuesto entonces, Ep pasa a ser negativo, si son el mismo tipo de carga luego, Ep es positiva.
Si Ep es positivo, entonces, la energía potencial eléctrica es inversamente proporcional a la distancia d.
Si Ep es negativa, entonces, la energía potencial eléctrica es directamente proporcional a la distancia d.
En la Figura 1 y Figura 2, cargas iguales se repelen entre sí, por lo tanto las fuerzas externas no funciona para disminuir la distancia entre ellos. Por el contrario, en la Figura 3, las cargas se atraen otra distancia, entre ellos se reduce por las fuerzas eléctricas, y no hay necesidad de otras fuerzas externas.
Ejemplo: Sistema que figuran a continuación se compone de los cargos, 10q, 8q y 5q-. Fin del total de la energía potencial eléctrica del sistema.
Ejemplo: Sistema que figuran a continuación se compone de los cargos, 10q, 8q y 5q-. Fin del total de la energía potencial eléctrica del sistema.
Potencial eléctrico
El potencial eléctrico es la energía potencial eléctrica por unidad de carga. Se le conoce como tensión en general, representada por V y tiene unidad de voltios (julio / C).
El potencial eléctrico es la energía potencial eléctrica por unidad de carga. Se le conoce como tensión en general, representada por V y tiene unidad de voltios (julio / C).
Carga 1C es llevado hasta el punto A desde el infinito. El trabajo hecho aquí se llama potencial de q en A. El potencial eléctrico se encuentra en la fórmula;
V = k.q / d
V es una magnitud escalar. Si q es negativa, entonces V se convierte en negativo, o si q es positiva, entonces V se convierte en positivo.
Superficies que tienen el potencial iguales se llaman superficies equipotenciales.
V = k.q / d
V es una magnitud escalar. Si q es negativa, entonces V se convierte en negativo, o si q es positiva, entonces V se convierte en positivo.
Superficies que tienen el potencial iguales se llaman superficies equipotenciales.
Potencial de una esfera cargada
Potencial en la superficie es igual a la potencial dentro de la esfera. Puesto que no hay fuerza que actúa dentro de la esfera, el trabajo no se hace para llevar la carga desde la superficie hasta el interior de la esfera. A medida que la distancia desde la superficie de la esfera de aumentar, disminuye el potencial. Cuadro que se presenta a continuación muestra el cambio en el potencial de la esfera interior, la superficie y el exterior. Como puede ver, el potencial es constante y dentro de la superficie de la esfera, sin embargo, disminuye con la distancia fuera de ella.
Potencial en la superficie es igual a la potencial dentro de la esfera. Puesto que no hay fuerza que actúa dentro de la esfera, el trabajo no se hace para llevar la carga desde la superficie hasta el interior de la esfera. A medida que la distancia desde la superficie de la esfera de aumentar, disminuye el potencial. Cuadro que se presenta a continuación muestra el cambio en el potencial de la esfera interior, la superficie y el exterior. Como puede ver, el potencial es constante y dentro de la superficie de la esfera, sin embargo, disminuye con la distancia fuera de ella.
Diferencia de potencial entre dos puntos
El trabajo realizado contra el campo eléctrico para mover la unidad de carga de un punto a otro se llama diferencia de potencial entre estos dos puntos. Esta diferencia se encuentra por las diferencias de potencial de este último punto, desde el punto inicial. Si tomamos el punto de carga de A a B, entonces la diferencia de potencial se encuentra por la fórmula;
El trabajo realizado contra el campo eléctrico para mover la unidad de carga de un punto a otro se llama diferencia de potencial entre estos dos puntos. Esta diferencia se encuentra por las diferencias de potencial de este último punto, desde el punto inicial. Si tomamos el punto de carga de A a B, entonces la diferencia de potencial se encuentra por la fórmula;
Ejemplo: Encuentra la diferencia de potencial entre los puntos A y B, en términos de VAB kq / r?
Ejemplo: Si el campo eléctrico total producido por Q y Q 'es como en la imagen a continuación, encontrar el potencial eléctrico de la A.
Escala de temperatura absoluta
Si introducimos el recipiente cilíndrico en un medio a diferentes temperaturas encontraremos que a medida que el gas se calienta su presión crece si mantenemos el volumen contante, y que su volumen crece si se mantiene la presión constante. De la misma forma, tanto el volumen como la presión disminuyen cuando el gas de enfría. Si detallamos en el asunto, hemos construido un termómetro, es decir, un sistema que cambia una de sus magnitudes medibles con el cambio de temperatura.
Nuestro termómetro está notablemente cerca de ser un termómetro universal ya que la experimentación ha demostrado que la constante de proporcionalidad es la misma para todos los gases siempre que sus densidades sean muy bajas (enrarecidos). En este estado de dilución, los gases se pueden considerar gases ideales, y nos permiten establecer una escala universal de temperatura. El grado de enrarecimiento necesaria del gas será cuestión de cuan preciso queremos que sea nuestro termómetro.
En la figura 2 se plotea la presión de un gas contra nuestra escala de temperatura, es decir en un termómetro de gas ideal a volumen constante. La parte del gráfico en las cercanías de la temperatura y presión cero aparece con linea de puntos debido a que en esa zona de temperaturas tan bajas nuestro termómetro no funciona al licuarse o congelarse el gas, y el tramo en linea de puntos es una extrapolación.
Si observamos el gráfico de la figura 2 nos podemos dar cuenta que la temperatura de un cuerpo no puede bajar indefinidamente y esta solo puede alcanzar aquel valor mínimo en el que la presión es cero. Si partimos del hecho de que la presión de un fluido sobre una superficie se debe al choque de las moléculas del fluido sobre la superficie, cuando la presión es cero las moléculas están en reposo, su energía cinética es cero, una condición límite poco menos que imposible en la práctica. Este punto hipotético de energía cinética cero produce el llamado cero absoluto de temperatura.
Ahora ajustemos la temperatura T = 0 en el lugar en el que la presión p se hace cero (si esto fuera posible), y como los experimentos indican que:
p = (una constante)T (ecuación 1)
necesitamos definir T en algún otro punto. El segundo punto establecido en 1968 fue el punto triple del agua por acuerdo internacional. Este es el punto donde el agua coexiste como vapor, líquido y sólido y se le asignó el valor de 273.16 K en la que la K significa kelvin, y la escala así nacida se llama escala Kelvin. La denominación de kelvin a la escala se hizo en honor a Sir Willian Thomson, Lord Kelvin que desarrolló importantes trabajos en el siglo XIX en los fenómenos térmicos.
tc = T - 273.15
Donde T es la temperatura en la escala Kelvin y tc es la temperatura en la escala Celsius. La escala Celsius también se conoce como escala centígrada.
Otra escala de temperatura usada en la práctica es la escala Fahrenheit en la cual la temperatura tf se mide en grados Fahrenheit (ºF) y fue establecida con la temperatura corporal humana en mente. En esta escala la temperatura de fusión del hielo corresponde a 32ºF, la temperatura del cuerpo humano es de unos 100ºF y la temperatura de ebullición del agua es 112ºF. La relación entre las escalas Fahrenheit y la Kelvin es:
tf = 9/5T - 459.67
No hay comentarios:
Publicar un comentario