Temas de física

Energía mecánica

Descripción

Cuando cargamos un objeto pesado sabemos por experiencia que para hacerlo tenemos que realizar un determinado esfuerzo muscular a fin de sostenerlo a cierta altura, y sabemos además que si lo soltamos sin cuidado puede el objeto, de hecho, caernos en un pie y producir una lesión dolorosa. Intuitivamente nos damos cuenta de que el cuerpo suspendido tiene una cierta cantidad de energía "en potencia" que puede convertirse muy fácilmente en un movimiento, y que este movimiento también tiene la energía capaz de producir la lesión a la que nos referimos. Pues bien, del experimento se puede deducir cualitativamente que la energía contenida en el objeto suspendido y luego dejado caer (que llamaremos energía mecánica) se puede manifestar de dos maneras: como una energía potencial latente cuando el cuerpo está suspendido y no se mueve; y otra forma de la energía cuando se mueve que se llama energía cinética.

Lo mismo sucede para el caso de un tanque elevado lleno de agua y del cual sale un tubo provisto de una llave de paso. Cuando la llave está cerrada no hay movimiento del agua, toda su energía, debido a la altura, es energía potencial, está latente, esperando que abramos la llave para producir una corriente de agua en movimiento, y por tanto con cierta energía cinética capaz, por ejemplo, de mover un dispositivo de riego por aspersión.
 
Veamos ahora otra situación, supongamos que uno de los carros ha sido llevado por un sistema mecánico a su punto más alto en una montaña rusa, allí, el carro tiene su máxima energía potencial, cuando emprende la primera carrera de descenso va ganando velocidad y por tanto aumentando su energía cinética. Una vez llegado al punto mas bajo, tiene una gran velocidad y alta energía cinética, y puede, por tanto, iniciar la subida de la próxima cuesta, al hacerlo va perdiendo velocidad, pero ganando en altura, es decir su energía cinética se va transformando de nuevo en energía potencial hasta llegar a la nueva cima y repetir el proceso en todos los valles y crestas de la montaña rusa. Esto significa que ambas formas de energía mecánica son transformables mutuamente, tanto en una dirección como en la otra.

Las mediciones cuidadosas hechas por los hombres de ciencia a los largo de los años han demostrado, que cuando se considera el caso ideal de que el sistema no tiene pérdidas por resistencias externas que consuman parte de la energía contenida inicialmente, esta solo puede ser transformada de una forma a la otra indefinidamente manteniendo el total energético constante. Este principio se conoce como la Ley de la Conservación de la Energía Mecánica, y es uno de los preceptos físicos mas significativos e importantes, al permitir interpretar multitud de situaciones en muchos campos de la ciencia.

Matemáticamente el principio de la conservación de la energía podía formularse así:

E = E_p + E_c = K        (ecuación 1)

Es decir la energía total E, es la suma de la energía potencial, E_p y la energía cinética E_c , e igual a una constante K.

Evaluación cuantitativa de la energía mecánica

Sin entrar en complicadas deducciones matemáticas vamos a relacionar a continuación las expresiones que sirven para evaluar la magnitud de la energía mecánica en un sistema uni-dimensional:

Energía cinética

La energía cinética de un objeto en movimiento responde a la expresión:

      (ecuación 2)

Donde v es la velocidad del objeto, y m su masa. Note que la unidad de la energía cinética es kg·m² / s²  la que ha recibido el nombre particular de joule en honor a James Joule que hizo importantes trabajos en este campo. 

Energía potencial

La energía potencial dependerá del sistema en cuestión y tiene varias expresiones de cálculo de acuerdo a esto:

Aplicación a la gravedad

Para un cuerpo suspendido a un altura y, de la superficie de la Tierra y bajo la acción de la gravedad; considerando la altura de la superficie como y = 0,  adquiere la forma:

E_p = mgy        (ecuación 3)    

Donde: m es la masa del cuerpo; y g es la aceleración de la gravedad.

Un análisis dimensional simple le dirá que la energía potencial también se expresa en joules. En la práctica la magnitud y generalmente es la altura del objeto medida desde el suelo (h), de modo que la energía potencial debido a la gravedad también puede expresarse como;

E_p = mgh

Aplicación a un resorte

Figura 1

Veamos el caso ideal de una masa m solidaria al extremo de un resorte horizontal donde no hay influencia de la gravedad, como se muestra en la figura 1.

Originalmente el muelle está en reposo, y el sistema está en equilibrio, si utilizamos una fuerza externa y estiramos o comprimimos el resorte, en este se acumula cierta cantidad de energía potencial, si llamamos x a la distancia recorrida por la masa, en la posición de estirado o comprimido el valor dex será máximo pero su velocidad será cero. Si en ese instante lo soltamos, la fuerza del resorte mueve la masa buscando de nuevo la posición de equilibrio, la velocidad de la masa comenzará a crecer y por lo tanto aumenta su energía cinética. Como sabemos que la energía total se conserva, el incremento de la energía cinética se hace a expensas de la disminución de la energía potencial inicial.

Al pasar por la posición de equilibrio, la masa tendrá una alta energía cinética y prosigue su camino al lado contrario, ahora la fuerza del resorte se opone al movimiento y la masa comienza a bajar de velocidad, la energía cinética baja y se recupera la potencial. La masa se detiene de nuevo en la posición -x, toda la energía es ahora de nuevo potencial y la cinética es cero. Este proceso se repite como un movimiento oscilatorio armónico con una constante transformación de la energía entre uno y otro tipo.

Para simplificar las situaciones donde se utilizan resortes, siempre se consideran estos sin masa, y se asume que la fuerza ejercida por el resorte es proporcional al valor de x, lo que no se aparta mucho de la realidad.

Esta proporcionalidad se puede expresa como:

F = kx         (ecuación 4)

Donde k es la constante del resorte y depende se su geometría y dimensiones.

La expresión de la energía potencial de un resorte es entonces:

         (ecuación 5) 

Ya hemos dicho arriba que la energía puede manifestarse de diversas formas, entre estas están: la energía calórica contenida en un cuerpo caliente; la energía química presente en los enlaces químicos de las sustancias, como por ejemplo, la que se libera como radiaciones elecromagnéticas (básicamente calor y luz) durante la combustión al romperse ciertos enlaces de mayor energía y formarse otros de menor energía liberando la diferencia; y la energía eléctrica que puede estar contenida en un acumulador o una pila.

La energía mecánica de un objeto está asociada a su velocidad y su posición. Resulta imposible observar la energía mecánica de un objeto. Sin embargo, podemos estudiar la energía mecánica cuando se transforma de una forma a otra o cuando se transfiere de un lugar a otro. A esta transformación o transferencia de energía la llamamos trabajo. Normalmente el concepto trabajo es asociado al esfuerzo físico o mental a través del cual en ocasiones obtenemos una remuneración económica. Sin embargo, en la ciencia trabajo se refiere única y exclusivamente a la transformación o transferencia de energía.

Consideremos un objeto que se mueve cierto desplazamiento “d”, bajo la acción de una fuerza “F”, constante. El trabajo realizado por la fuerza se define como el producto de la magnitud de la fuerza que actúa en dirección del desplazamiento y la magnitud del desplazamiento.

W = F d

De acuerdo a la definición de trabajo, una fuerza realiza trabajo en un objeto cuando las siguientes dos condiciones se cumplen:

1. el objeto se desplaza
2. la fuerza es en la dirección del desplazamiento

Si aplicamos una fuerza sobre un objeto y el mismo no se desplaza, podemos concluir que el trabajo realizado es cero. Aunque nos agotemos físicamente, no se habrá realizado trabajo.

La primera ley de Newton establece que: “Un objeto en reposo o en movimiento con velocidad constante, es decir en línea recta con rapidez constante, permanecerá así hasta que una fuerza externa no balanceada actúe sobre él”. Es decir, para cambiar el movimiento de un objeto, hace falta la acción de una fuerza. Esta fuerza causará un cambio en el estado mecánico del objeto, por lo que podemos concluir que la misma realiza trabajo. En otras palabras, ocurre una transferencia o transformación de energía. Esta energía transferida o transformada producirá un cambio observable en el movimiento del objeto.

Cuando una fuerza no balanceada actúa sobre un objeto, este acelera (F = ma). Si el objeto se desplaza una cierta magnitud “d” entonces la fuerza habrá realizado trabajo.

W = F d

W = (m a) d

Mientras la fuerza actúa en el objeto; ésta realiza trabajo en el objeto transfiriendo energía. El desplazamiento está dado por la ecuación

d = ½ (vf + vi)t

y la definición de aceleración es

a = (vf – vi) / t

entonces

W = [m (vf – vi) / t] [½ (vf + vi)t]

W = ½ m [(vf – vi) (vf + vi)]

W = ½ m (vf²– vi²)

W = (½ m vf²) – (½ m vi²)

a cada término lo llamamos energía cinética (k).

La energía cinética es la energía mecánica asociada al movimiento de un objeto. Cuando un objeto se mueve, tiene energía cinética debido a su velocidad. En términos generales a mayor velocidad mayor energía.

k = ½ m v²

Fíjate que el trabajo es igual a la diferencia en la energía cinética de un objeto.

W = (½ m vf²) – (½ m vi²)

W = kf - ki

Si el trabajo es positivo (W > 0), implica que la energía cinética final, kf, es mayor que la energía cinética inicial, ki. Esto significa que el objeto aumentaría su velocidad, siendo la fuerza en dirección del desplazamiento.

Si el trabajo es negativo (W < 0), implica que la energía cinética final, kf, es menor que la energía cinética inicial, ki. Esto significa que el objeto disminuiría su velocidad, siendo la fuerza en dirección opuesta al desplazamiento.

Si el trabajo es cero (W = 0), implica que la energía cinética final, kf, es igual a la energía cinética inicial, ki. Esto significa que el objeto mantendrá una velocidad constante o igual a cero.
               
     
     
Cuando la fuerza F actúa sobre el bloque m logrando un desplazamiento d, decimos que la fuerza ha realizado trabajo sobre el bloque. La magnitud del trabajo realizado está dado por W=Fd.
   
        
La fuerza aplicada por el niño realizará trabajo sobre la caja, solo si ésta comienza a desplazarse.
   
       
La fuerza de gravedad actúa sobre el libro atrayéndolo hacia el centro de la tierra y realizando trabajo en el libro. Como la fuerza es en dirección del desplazamiento, el trabajo realizado por la fuerza de gravedad es positivo. Esto significa que la velocidad del libro aumentará según vaya cayendo.   

Conservación de la energía mecánica

Para sistemas abiertos formados por partículas que interactúan mediante fuerzas puramente mecánicas o campos conservativos la energía se mantiene constante con el tiempo:

.

Donde:

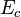, es la energía cinética del sistema.

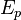, es la energía potencial gravitacional del sistema.

, es la energía potencial elástica del sistema.

Es importante notar que la energía mecánica así definida permanece constante si únicamente actúan fuerzas conservativas sobre las partículas. Sin embargo,existen ejemplos de sistemas de partículas donde la energía mecánica no se conserva:

• Sistemas de partículas cargadas en movimiento. En ese caso los campos magnéticos no derivan de un potencial y la energía mecánica no se conserva, ya que parte de la energía mecánica «se transforma» en energía del campo electromagnético y viceversa.
• Sistemas termodinámicos que experimentan cambios de estado. En estos sistemas la energía mecánica puede transformarse en energía térmica o energía interna. Cuando hay producción de energía térmica, en general, existirá disipación y el sistema habrá experimentado un cambio reversible (aunque no en todos los casos). Por lo que en general estos sistemas aún pudiendo experimentar cambios reversibles sin disipación tampoco conservarán la energía mecánica debido a que la única variable conservada es la energía interna.
• Mecánica de medios continuos disipativos que involucran fluidos disipativos o sólidos anelásticos (plasticidad, viscoelasticidad, etc), que involucran la aparición de deformaciones irreversibles y por tanto disipación, aparición de calor o cambios internos irreversibles, donde la variación de entropía no es nula.