Epónimos relacionados con las matemáticas

método de Broyden es un método cuasinewtoniano para la solución numérica de sistemas ecuaciones no lineales con más de una variable. Fue descrito originalmente por C. G. Broyden en 1965.¹

Para hallar la solución del sistema de ecuaciones ${\displaystyle \displaystyle f_{i}(x_{1},x_{2},...,x_{n})=0}$, con ${\displaystyle i=1,2,...,n}$, el método de Newton emplea el jacobiano ${\displaystyle \displaystyle J}$ en cada iteración, además de calcular su inversa. Sin embargo, computar ese jacobiano es una operación difícil y costosa. La idea que subyace en el método de Broyden consiste en computar el jacobiano entero solamente en la primera iteración, y llevar a cabo una actualización de rango 1 en las demás iteraciones.

${\displaystyle f_{i}(x_{1},x_{2},...,x_{n})}$ se supone continua y diferenciable en un conjunto abierto en ${\displaystyle \mathbb {R} ^{n}}$ con derivadas parciales continuas en ese abierto.²

En 1979, Gay demostró que, cuando se aplica el método de Broyden a un sistema lineal, se requieren 2n pasos.

Descripción del método

El método de Broyden considera el método de la secante y establece una generalización de él para el espacio multidimensional.

El método de la secante sustituye la primera derivada ${\displaystyle \displaystyle f'(x_{n})}$ por la aproximación de diferencia finita

${\displaystyle f'(x_{n})\simeq {\frac {f(x_{n})-f(x_{n-1})}{x_{n}-x_{n-1}}}}$

y procede según el método de Newton:

${\displaystyle x_{n+1}=x_{n}-{\frac {1}{f'(x_{n})}}f(x_{n})}$

Broyden establece una generalización de esa fórmula para un sistema de ecuaciones mediante una sustitución de ${\displaystyle {\frac {1}{f'(x_{n})}}}$ por la inversa del jacobiano ${\displaystyle \displaystyle J}$. Éste se determina por medio de la ecuación de la secante (la aproximación de diferencia finita):

${\displaystyle J_{n}\cdot (x_{n}-x_{n-1})\simeq F(x_{n})-F(x_{n-1})}$

Sin embargo, esta ecuación está infradeterminada por más de una dimensión.

Broyden sugiere un procedimiento que consta de los siguientes 3 pasos:

1) Emplear la aproximación del jacobiano ${\displaystyle \displaystyle J_{n-1}}$

2) Tomar la solución de la ecuación de la secante que suponga la modificación mínima de ${\displaystyle \displaystyle J_{n-1}}$ (entendiendo por mínima que se dé una minimización de la norma de Frobenius ${\displaystyle \displaystyle \|J_{n}-J_{n-1}\|_{F}}$)

${\displaystyle J_{n}=J_{n-1}+{\frac {\Delta F_{n}-J_{n-1}\Delta x_{n}}{\|\Delta x_{n}\|^{2}}}\Delta x_{n}^{T}}$

3) Continuar según el método de Newton:

${\displaystyle x_{n+1}=x_{n}-J_{n}^{-1}F(x_{n}).}$

En esa última fórmula,

${\displaystyle \displaystyle x_{n}=(x_{1}[n],...,x_{k}[n])}$

y

${\displaystyle \displaystyle F_{n}(x)=(f_{1}(x_{1}[n],...,x_{k}[n]),...,f_{k}(x_{1}[n],...,x_{k}[n])}$

son vectores columna de k elementos en un sistema de k dimensiones.

Así:

${\displaystyle \Delta x_{n}={\begin{bmatrix}x_{1}[n]-x_{1}[n-1]\\...\\x_{k}[n]-x_{k}[n-1]\end{bmatrix}}\quad {\text{y}}\quad \Delta F_{n}={\begin{bmatrix}f_{1}(x_{1}[n],...,x_{k}[n])-f_{1}(x_{1}[n-1],...,x_{k}[n-1])\\...\\f_{k}(x_{1}[n],...,x_{k}[n])-f_{k}(x_{1}[n-1],...,x_{k}[n-1])\end{bmatrix}}.}$

Broyden sugiere también la fórmula de Sherman-Morrison para actualizar directamente el inverso de la aproximación del jacobiano por la aproximación de diferencia finita:

${\displaystyle J_{n}^{-1}=J_{n-1}^{-1}+{\frac {\Delta x_{n}-J_{n-1}^{-1}\Delta F_{n}}{\Delta x_{n}^{T}J_{n-1}^{-1}\Delta F_{n}}}(\Delta x_{n}^{T}J_{n-1}^{-1})}$

Este último se conoce como el « buen método de Broyden».

Se puede obtener a partir de él una técnica similar empleando una modificación ligeramente distinta de ${\displaystyle J_{n-1}}$ que minimiza en su lugar ${\displaystyle \displaystyle \|J_{n}^{-1}-J_{n-1}^{-1}\|_{F}}$

Tal sería el llamado « mal método de Broyden»:

${\displaystyle J_{n}^{-1}=J_{n-1}^{-1}+{\frac {\Delta x_{n}-J_{n-1}^{-1}\Delta F_{n}}{\Delta F_{n}^{T}\Delta F_{n}}}\Delta F_{n}^{T}}$

Pero, en cuanto a lo de « mal método», véase "A faster Broyden method" ("Un método de Broyden más rápido").⁴

Se han sugerido muchos otros procedimientos cuasinewtonianos en el campo de la optimización, en el que se busca un máximo o un mínimo hallando la raíz de la primera derivada, o el gradiente si se trata de un espacio multidimensional. Se califica al jacobiano del gradiente de «hessiano», y es simétrico, lo que añade restricciones a la hora de llevar a cabo su actualización.

Fórmula de Sherman Morrison⁵

Si A es una matriz no singular y ${\displaystyle x}$ y ${\displaystyle y}$ son vectores con ${\displaystyle y^{t}A^{-1}x\neq -1}$ entonces ${\displaystyle A+xy^{t}}$ es no singular y

${\displaystyle (A+xy^{t})^{-1}=A^{-1}-{A^{-1}xy^{t}A^{-1} \over 1+y^{t}A^{-1}x}}$

Esta fórmula de Sherman-Morrison permite calcular la inversa de una matriz a partir de la inversa del Jacobiano, es por eso que solo se requiere en la primera iteración del método de Broyden, ya que para las iteraciones subsecuentes se va empleando la aproximación de la iteración anterior.

Imagen 1

El método de Broyden es un método cuasi-newtoniano, se denomina así a los métodos que se aproxima a la matriz jacobiana mediante recurrencia que la relacionen con el  valor que tome en iteración anteriores. Para explicar el método consideremos f(x)=0 un sistema de ecuaciones lineales entonces es de la forma Ax-b=0. Si se restan dos valores de f(x) en dos puntos sucesivos de la iteración x_k-1 y x_k, se tiene que:

f(x_k)-f(x_k-1)=A(x_k-x_k-1)

Por el contrario en el caso no lineal la igualdad anterior no se cumple aunque se puede lograr, eligiendo adecuadamente A, que 

f(x_k)-f(x_k-1)≈A_k(x_k-x_k-1)

en si no el método no se ve muy complicado de lo expuesto hasta ahora, pero considerando los calculo que se realizan por cada iteración se ve la debilidad del método, para calcular el jacobiano asociado a un sistema de n ecuaciones no lineales requiere determinar y evaluar n derivadas parciales. Cuando no es práctico efectuar la evaluación exacta, podemos usar la aproximacion de diferencia finita a las derivadas parciales

 ∂f_j(xⁱ)/ ∂x_k ≈ (f_j(xⁱ+e_kh)-f_j(xⁱ))/h

Sin embargo está aproximación requiere efectuar, al menos, n² evaluciones de funciones escalares para aproximar la matriz jacobiana y no disminuye la cantidad de cálculos, casi siempre es necesario O(n³) para resolver el sistema. Por lo tanto, el total de cálculos que se requiere para una sola iteración del método es almenos n²+n evaluaciones de funciones escalares(n² para evaluar la matriz jacobiana y n para evaluar f), junto con O(n³) operaciones aritmeticas para resolver el sistema lineal. Asi la cantidad de cálculos aumenta conforme aumenta la cantidad de ecuaciones del sistema en el caso del método de Newton pero con el método de Broyden tiene una convergencia superlineal.

Generalizando para mas dimensiones la aproximación por la derivada de imagen 1 obtenemos

J_k(x_k-x_k-1) ≈ f(x_k)-f(x_k-1)

entonces según el método de newton las iteraciones seran segun

x_k = x_k-1 + J_k^-1[ f(x_k) ]

y para cada iteración usamos la siguiente formula propuesta por broyden para hallar el jacobiano J

J_k = J_k-1 + [ (∇y_k-J_k-1∇s_k) / ||∇s_k||² ] ∇s_k^T

donde

∇y = f(x_k)-f(x_k-1)    ∇s_k = x_k-x_k-1

 Curva de Agnesi (pronunciado 'añesi'), también llamada impropiamente bruja de Agnesi, es conocida así por la matemática italiana Maria Gaetana Agnesi). ¹ Se trata de una curva abierta que se construye de la forma siguiente:

Generación de la curva.

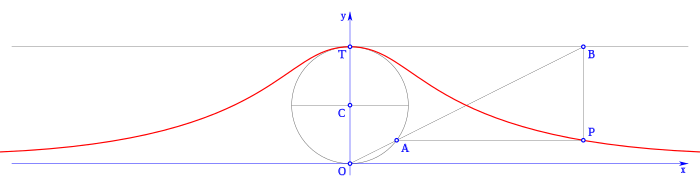
A partir de una circunferencia, y un punto cualquiera O de la circunferencia, siendo T el punto diametralmente opuesto a O. Para cualquier otro punto A de la circunferencia, la prolongación de la línea secante OA corta a la perpendicular a OT que pasa por T en B. La línea paralela a OT que pasa por B, y la línea perpendicular a OT que pasa por A se cortan en P. Tomando como variable el punto A se define que la curva de los puntos P es el de bruja.

La asíntota de esta curva es la línea tangente a la circunferencia que pasa por el punto O.

Historia

Esta curva fue estudiada por Pierre de Fermat en 1630, por Guido Grandi en 1703 y por Maria Gaetana Agnesi en 1748.

Grandi llamó a la curva versoria, del latín vertere, que significa virar o girar; versiera en italiano es un término naval que identifica el cabo o cuerda que hace girar la vela. María Gaetana Agnesi se refirió a esta curva como la versiera, añadiéndole el artículo femenino la; de esta manera, la versiera di Agnesi significa la curva de Agnesi.

Los estudios de Agnesi sobre esta curva fueron traducidos al inglés por el profesor de la Universidad de Cambridge John Colson, quien al tener escaso conocimiento del italiano confundió versiera con avversiera, que en italiano significa 'diablesa', 'demonia'. Por eso tradujo el término al inglés como witch (hechicera, bruja), y esta anécdota ha hecho que haya quien guste de llamar "bruja" a esta curva. En otros idiomas se habla de loci (en latín, 'lugares' geométricos) de Agnesi. En italiano se denomina versiera, como debe ser.^2 3

Ecuaciones

La curva de Agnesi puede representarse analíticamente como función en el plano xy, tanto en su forma cartesiana y= f(x) como paramétricamente.

Ecuación cartesiana

Tomando el punto O como origen de coordenada, y que T en el lado positivo del eje y, y tomando como radio de la circunferencia el valor a.

Según la figura tenemos las siguientes ecuaciones, por la definición de tangente en el triángulo OAE rectángulo en E y el triángulo OBD rectángulo en D, Semejantes entre sí:

${\displaystyle \tan \alpha ={\cfrac {\overline {AE}}{\overline {EO}}}={\cfrac {\overline {BD}}{\overline {DO}}}}$

En el triángulo ACF rectángulo en F, y por el teorema de Pitágoras, tenemos que

${\displaystyle {({\overline {AC}})}^{2}={({\overline {AF}})}^{2}+{({\overline {CF}})}^{2}}$

Podemos ver también las siguientes igualdades:

${\displaystyle \left\{{\begin{array}{rcl}{\overline {CO}}&=&{\overline {CF}}+{\overline {FO}}\\{\overline {FO}}&=&{\overline {AE}}\\{\overline {BD}}&=&2\cdot {\overline {CO}}\\{\overline {AF}}&=&{\overline {EO}}\\{\overline {AC}}&=&{\overline {CO}}=a\\{\overline {AE}}&=&{\overline {PD}}=y\\{\overline {DO}}&=&x\\\end{array}}\right.}$

Que se puede resumir en las relaciones:

${\displaystyle \left\{{\begin{array}{l}\tan \alpha ={\cfrac {y}{\overline {EO}}}={\cfrac {2a}{x}}\\\left.{\begin{array}{l}a^{2}={({\overline {EO}})}^{2}+{({\overline {CF}})}^{2}\\a={\overline {CF}}+y\end{array}}\right\}\rightarrow {({\overline {EO}})}^{2}=y\;(2a-y)\end{array}}\right.}$

Partiendo de las ecuaciones deducimos:

${\displaystyle \left.{\begin{array}{l}{\cfrac {y}{\overline {EO}}}={\cfrac {2a}{x}}\\{({\overline {EO}})}^{2}=y\;(2a-y)\end{array}}\right\}\rightarrow {\cfrac {y}{\sqrt {y\;(2a-y)}}}={\cfrac {2a}{x}}}$

Elevando la ecuación al cuadrado tenemos:

${\displaystyle {\cfrac {y^{2}}{y\;(2a-y)}}={\cfrac {4a^{2}}{x^{2}}}\rightarrow {\cfrac {y}{2a-y}}={\cfrac {4a^{2}}{x^{2}}}\rightarrow {\cfrac {2a-y}{y}}={\cfrac {x^{2}}{4a^{2}}}\rightarrow {\cfrac {2a}{y}}-1={\cfrac {x^{2}}{4a^{2}}}}$

Operando con la expresión tendremos que:

${\displaystyle {\cfrac {2a}{y}}={\cfrac {x^{2}}{4a^{2}}}+1\rightarrow {\cfrac {2a}{y}}={\cfrac {x^{2}}{4a^{2}}}+{\cfrac {4a^{2}}{4a^{2}}}\rightarrow {\cfrac {2a}{y}}={\cfrac {x^{2}+4a^{2}}{4a^{2}}}}$

Que invirtiendo la fracción y simplificando dará como resultado:

${\displaystyle {\cfrac {y}{2a}}={\cfrac {4a^{2}}{x^{2}+4a^{2}}}\rightarrow y={\cfrac {8a^{3}}{x^{2}+4a^{2}}}}$

Entonces la curva tiene por ecuación cartesiana:

${\displaystyle y={\frac {8a^{3}}{x^{2}+4a^{2}}}}$

Nota: si tomamos a a=1/2, entonces la ecuación toma una forma muy sencilla:

${\displaystyle y={\frac {1}{x^{2}+1}}.}$

Ecuación paramétrica

Paramétricamente, si ${\displaystyle \alpha \,}$ es el ángulo entre OD y OB, o lo que es lo mismo entre OE y OA, medido en sentido trigonométrico, entonces la curva se define por las ecuaciones:

Partiendo, al igual que en la ecuación cartesiana, de:

${\displaystyle \left\{{\begin{array}{l}\tan \alpha ={\cfrac {y}{\overline {EO}}}={\cfrac {2a}{x}}\\{({\overline {EO}})}^{2}=y\;(2a-y)\end{array}}\right.}$

Primero despejaremos la x respecto de ${\displaystyle \alpha \,}$:

${\displaystyle \tan \alpha ={\cfrac {2a}{x}}}$

Con lo que fácilmente se puede ver, que:

${\displaystyle x={\cfrac {2a}{\tan \alpha }}=2a\cot \alpha }$

Ahora despejaremos la y respecto de ${\displaystyle \alpha \,}$, partiendo de:

${\displaystyle \left.{\begin{array}{l}\tan \alpha ={\cfrac {y}{\overline {EO}}}\\{({\overline {EO}})}^{2}=y\;(2a-y)\end{array}}\right\}\rightarrow \tan \alpha ={\cfrac {y}{\sqrt {y\;(2a-y)}}}}$

Sabiendo que:

${\displaystyle \tan \alpha ={\cfrac {\sin \alpha }{\cos \alpha }}}$

Tendremos:

${\displaystyle {\cfrac {\sin \alpha }{\cos \alpha }}={\cfrac {y}{\sqrt {y\;(2a-y)}}}}$

Elevando esta expresión al cuadrado, tendremos:

${\displaystyle {\cfrac {\sin ^{2}\alpha }{\cos ^{2}\alpha }}={\cfrac {y^{2}}{y\;(2a-y)}}\rightarrow {\cfrac {\sin ^{2}\alpha }{\cos ^{2}\alpha }}={\cfrac {y}{2a-y}}\rightarrow {\cfrac {\cos ^{2}\alpha }{\sin ^{2}\alpha }}={\cfrac {2a-y}{y}}\rightarrow {\cfrac {\cos ^{2}\alpha }{\sin ^{2}\alpha }}={\cfrac {2a}{y}}-1}$

Operando con la expresión:

${\displaystyle {\cfrac {2a}{y}}={\cfrac {\cos ^{2}\alpha }{\sin ^{2}\alpha }}+1\rightarrow {\cfrac {2a}{y}}={\cfrac {\cos ^{2}\alpha }{\sin ^{2}\alpha }}+{\cfrac {\sin ^{2}\alpha }{\sin ^{2}\alpha }}\rightarrow {\cfrac {2a}{y}}={\cfrac {\cos ^{2}\alpha +\sin ^{2}\alpha }{\sin ^{2}\alpha }}}$

Sabiendo que:

${\displaystyle 1=\sin ^{2}\alpha +\cos ^{2}\alpha \,}$

Tendremos:

${\displaystyle {\cfrac {2a}{y}}={\cfrac {1}{\sin ^{2}\alpha }}\rightarrow {\cfrac {y}{2a}}=\sin ^{2}\alpha \rightarrow y=2a\sin ^{2}\alpha }$

${\displaystyle x=2a\cot \alpha \,}$

${\displaystyle y=2a\sin ^{2}\alpha \,}$

Estas ecuaciones dependen del ángulo ${\displaystyle \alpha \,}$ y de la correspondiente función trigonométrica, veamos un forma paramétrica más sencilla eliminando las funciones trigonométricas.

Partimos de las ecuaciones:

${\displaystyle x={\cfrac {2a}{\tan \alpha }}}$

${\displaystyle y=2a\sin ^{2}\alpha \,}$

y sabemos que:

${\displaystyle \tan \alpha ={\cfrac {\sin \alpha }{\cos \alpha }}}$

haciendo el inverso:

${\displaystyle {\cfrac {1}{\tan \alpha }}={\cfrac {\cos \alpha }{\sin \alpha }}}$

por la relación del coseno respecto al seno:

${\displaystyle {\cfrac {1}{\tan \alpha }}={\cfrac {\sqrt {1-\sin ^{2}\alpha }}{\sin \alpha }}}$

aplicando la raíz al denominador:

${\displaystyle {\cfrac {1}{\tan \alpha }}={\sqrt {\cfrac {1-\sin ^{2}\alpha }{\sin ^{2}\alpha }}}}$

operando la fracción:

${\displaystyle {\cfrac {1}{\tan \alpha }}={\sqrt {{\cfrac {1}{\sin ^{2}\alpha }}-1}}}$

si llamamos t a:

${\displaystyle t={\cfrac {1}{\tan \alpha }}}$

tendremos que:

${\displaystyle t={\sqrt {{\cfrac {1}{\sin ^{2}\alpha }}-1}}}$

eliminando la raíz:

${\displaystyle t^{2}={\cfrac {1}{\sin ^{2}\alpha }}-1}$

operando:

${\displaystyle t^{2}+1={\cfrac {1}{\sin ^{2}\alpha }}}$

lo que resulta:

${\displaystyle \sin ^{2}\alpha ={\cfrac {1}{t^{2}+1}}}$

Con estos resultados y las ecuaciones originales, tenemos:

${\displaystyle \left.{\begin{array}{l}x={\cfrac {2a}{\tan \alpha }}\\\\y=2a\sin ^{2}\alpha \\{\cfrac {1}{\tan \alpha }}=t\\\sin ^{2}\alpha ={\cfrac {1}{t^{2}+1}}\end{array}}\right\}\longrightarrow \left\{{\begin{array}{l}x={2a}t\\y={\cfrac {2a}{t^{2}+1}}\end{array}}\right.}$

Con lo que tenemos las ecuaciones paramétricas:

${\displaystyle x={2a}t\,}$

${\displaystyle y={\cfrac {2a}{t^{2}+1}}\,}$

Donde t es un parámetro real, el signo de t es el mismo que el de x, así si t es negativo x será negativo, y si t es positivo x será también positivo. Independientemente del valor de t, y siempre tomara valores positivos, para t igual a cero, x valdrá cero é y valdrá 2a.

Cuando t tiende a infinito, x también tiende a infinito é y se hace cero.

Representación gráfica

La curva Bruja de Agnesi, definida por la función:

${\displaystyle y={\frac {8a^{3}}{x^{2}+4a^{2}}}}$

en el plano cartesiano xy, y donde el parámetro a es el radio de la circunferencia. También puede representarse según el parámetro d, diámetro de la circunferencia, donde d= 2a:

${\displaystyle y={\frac {8a^{3}}{x^{2}+4a^{2}}}\rightarrow \quad y={\frac {2^{3}a^{3}}{x^{2}+2^{2}a^{2}}}\rightarrow \quad y={\frac {(2a)^{3}}{x^{2}+(2a)^{2}}}\rightarrow \quad y={\frac {d^{3}}{x^{2}+d^{2}}}}$

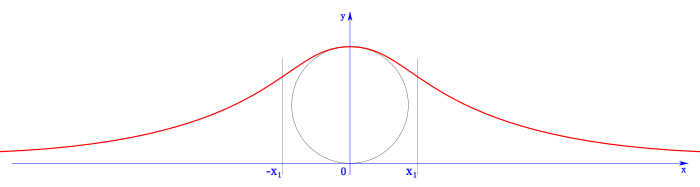
Estas dos expresiones son equivalentes, siendo la expresada según el diámetro d, más sencilla al carecer de coeficientes, las dos se pueden ver al consultar bibliografía y tiene por representación gráfica:

Estudio de la función.

Para estudiar la función de la curva Bruja de Agnesi, tomaremos su expresión cartesiana explícita:

${\displaystyle y={\frac {d^{3}}{x^{2}+d^{2}}}}$

donde d es el diámetro de la circunferencia. Pudiéndose ver las siguientes propiedades:

• Está definida para todos los valores de x reales:

${\displaystyle \forall x\in \mathbb {R} :\quad \exists y\in \mathbb {R} \quad /\quad y={\frac {d^{3}}{x^{2}+d^{2}}}}$

• Es una función par, simétrica respecto al eje y:

${\displaystyle \forall x\in \mathbb {R} :\quad f(x)=f(-x)\,}$

esto es:

${\displaystyle f(-x)={\frac {d^{3}}{(-x)^{2}+d^{2}}}={\frac {d^{3}}{x^{2}+d^{2}}}=f(x)}$

• Tiene por asíntota horizontal: y = 0

cuando x tiende a infinito la función se hace cero:

${\displaystyle {\underset {x\to +\infty }{L{\acute {\imath }}m}}\;{\frac {d^{3}}{x^{2}+d^{2}}}=0}$

y cuando x tiende a menos infinito también se hace cero:

${\displaystyle {\underset {x\to -\infty }{L{\acute {\imath }}m}}\;{\frac {d^{3}}{x^{2}+d^{2}}}=0}$

Derivada primera de la función

Partiendo de la función, calculamos su derivada:

${\displaystyle {\cfrac {dy}{dx}}\;{\frac {d^{3}}{x^{2}+d^{2}}}={\cfrac {-2d^{3}x}{(x^{2}+d^{2})^{2}}}}$

Esta derivada solo vale cero cuando x vale cero, por lo tanto puede presentar un extremo relativo para x = 0.

Derivada segunda de la función

Derivando nuevamente tendremos la segunda derivada de la función:

${\displaystyle {\cfrac {d^{2}y}{dx^{2}}}\;{\frac {d^{3}}{x^{2}+d^{2}}}={\cfrac {dy}{dx}}\;{\cfrac {-2d^{3}x}{(x^{2}+d^{2})^{2}}}={\cfrac {2d^{3}(3x^{2}-d^{2})}{(x^{2}+d^{2})^{3}}}}$

La segunda derivada valdrá cero cuando:

${\displaystyle 3x^{2}-d^{2}=0\;}$

Esto es:

${\displaystyle 3x^{2}=d^{2}\;}$

despejando la x, tenemos:

${\displaystyle x^{2}={\frac {d^{2}}{3}}\;}$

Lo que resulta:

${\displaystyle x=\pm {\frac {d}{\sqrt {3}}}\;}$

Para los valores:

${\displaystyle x={\frac {d}{\sqrt {3}}}\quad x=-{\frac {d}{\sqrt {3}}}}$

La función presenta puntos de inflexión.

Si llámanos:

${\displaystyle x_{1}={\frac {d}{\sqrt {3}}}}$

Podemos ver que en el intervalo: ${\displaystyle (-\infty ,-x_{1})\;}$ la función es convexa, en el intervalo ${\displaystyle (-x_{1},x_{1})\;}$ es cóncava y en ${\displaystyle (x_{1},\infty )\;}$ convexa, los puntos ${\displaystyle -x_{1},x_{1}\;}$ son puntos de inflexión y para ${\displaystyle x=0\;}$ presenta un máximo.

Puntos de inflexión

Los puntos de inflexión son

${\displaystyle B,C(\pm {\frac {d}{\sqrt {3}}},{\frac {3d}{4}})}$

, la inclinación de la curva en estos puntos es

${\displaystyle tg\phi =\mp {\frac {3{\sqrt {3}}}{8}}}$

⁴

Propiedades

• La zona comprendida entre la bruja y su asíntota es cuatro veces el área del círculo (es decir, ${\displaystyle 4\pi a^{2}\,}$)

• El volumen de la revolución de la bruja, tomando como eje su asíntota, es ${\displaystyle 4\pi 2a^{3}\,}$

• El centroide de la curva se encuentra en ( ${\displaystyle 0,{\frac {a}{2}}}$).

Aplicaciones

La bruja de Agnesi encuentra aplicación en la descripción física de los fenómenos de resonancia, por ejemplo, un átomo afectado por una radiación monocromática, emite radiación cuya intensidad depende de la frecuencia de la radiación emitida, y la relación entre los dos radiaciones viene dada por la bruja de Agnesi, con el máximo en la longitud de onda de luz incidente.

En Estadística, la distribución de Cauchy de una variable aleatoria se expresa por una bruja de Agnesi.