Matemáticas - Polinomios

función constante a aquella función matemática que toma el mismo valor para cualquier valor de la variable independiente. Se la representa de la forma:¹

${\displaystyle f(x)=c\,}$

Gráfica de una función lineal

Funciones reales de una variable real

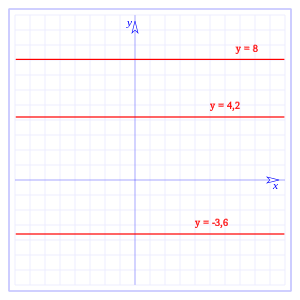
Como se puede ver es una recta horizontal en el plano cartesiano, en la gráfica la hemos representado en el plano, pero, como se puede ver la función no depende de x, si hacemos:

${\displaystyle y=f(x)\,}$

tenemos:

${\displaystyle y=c\,}$

donde c tiene un valor constante, en la gráfica tenemos representadas:

${\displaystyle y=8\,}$

${\displaystyle y=4,2\,}$

${\displaystyle y=-3,6\,}$

Como la variable dependiente y no depende de x tenemos que:

${\displaystyle {\frac {dy}{dx}}=0}$

la variación de y respecto a x es cero

La integral de la función constante:

${\displaystyle y=c\,}$

es:

${\displaystyle Y=\int _{a}^{b}c\,dx\;\rightarrow \quad Y=c\;\int _{a}^{b}dx\;\rightarrow \quad Y=c\;x{\Big ]}_{a}^{b}\;\rightarrow \quad Y=c\;(b-a)}$

La función constante como un polinomio en x

Si un polinomio general, que tiene la forma:

${\displaystyle f(x)=\sum _{i=0}^{n}a_{i}x^{i}.}$

una función constante cumple esta expresión con n= 0, es un polinomio de grado 0.

${\displaystyle f(x)=\sum _{i=0}^{0}a_{i}x^{i}.}$

que es lo mismo que:

${\displaystyle f(x)=ax^{0}=a\,}$

que corresponde al término independiente del polinomio.

Una función f es constante si la variable dependiente y toma el mismo valor a para cualquier elemento del dominio (variable independiente x).

En términos matemáticos, la función f es constante si para cualquier par de puntos x₁ y x₂ del dominio tales que x₁<x₂, se cumple que f(x₁) = f(x₂).

La gráfica de una función constante es una recta paralela al eje de abscisas X.

También se puede definir una función constante a partir de la derivada. Una función f será constante si para todo punto x del dominio la derivada es nula, es decir f ’(x) = 0.

La derivada de la función constante es 0 porque no depende del valor de la variable independiente x.

Función constante en un intervalo

ANUNCIOS

Sean a y b dos elementos del dominio, tales que c < d forman el intervalo [c,d].

Una función es constante entre c y d si para cualquier par de puntos x₁ y x₂ del intervalo tales que x₁<x₂, se cumple que f(x₁) = f(x₂). Es decir, es constante en [c,d] si al aumentar la variable independiente x, la variable dependiente y permanece constante.

Ejemplo de función constante en un intervalo

Función constante en un punto

Sea una función f derivable en el punto p.

La función f es constante en un punto p si f ’(p) = 0. Es decir, es constante si la derivada es nula en p .

Ejemplo de función constante en un punto

Ejemplo de función constante en un intervalo

Sea la función f definida como:

Estudiar si la función f es constante en el intervalo [2,4].

En el intervalo [2,4] f está definida como f(x)=1, cuya derivada es nula: f‘(x)=0.

Al ser la derivada es 0 en todo el intervalo [2,4], podemos decir que la función f es constante en [2,4].

Ejemplo de función constante en un punto

Supongamos que tenemos la función f definida como:

Estudiar si la función f es constante en los puntos x=-1 y x=1.

En los puntos x=-1 y x=1 actua f como la función f(x)=2, siendo su derivada f ’(x)=0. Por tanto:

La derivada en los puntos es f ’(-1)=0 y f ’(1)=0, por lo que f es constante en x=-1 y x=1.

http://www.universoformulas.com/matematicas/analisis/funcion-constante/