Deducción de la fórmula de Bhaskara
La fórmula que nos permite determinar las raíces de un polinomio de segundo grado fue deducida por el famoso matemático indio Bhaskaracharya, más conocido como Bhaskara II.
Lo que se busca es determinar los valores para los cuales la ecuación
Demostración sencilla por cambio de variable
Se puede simplificar si aplicamos el cambio de variable y . Así la ecuación queda:
- Aplicamos el cambio de variable
- Sumamos para ajustar cuadrados, y pasamos n al otro lado
- Y lo contraemos de esta manera
- Aplicamos la raíz cuadrada a ambos lados
- Pasamos restando
- Deshaciendo la sustitución, y
- Y operando llegamos a la siguiente ecuación:
Demostración
- Partimos de la ecuación
- Multiplicamos por
- Sumamos
- Reordenamos para observar que es el cuadrado de la suma
- Y lo contraemos
- Aplicamos la raíz cuadrada a ambos lados
- Pasamos restando
- Y dividimos por
-
- discriminante de un polinomio es una cierta expresión de los coeficientes de dicho polinomio que es igual a cero si y solo si el polinomio tiene raíces múltiples en el plano complejo. Por ejemplo, el discriminante del polinomio cuadrático
- es .
El discriminante del polinomio cúbico- es .
Este concepto también se aplica si el polinomio tiene coeficientes en un cuerpo que no está contenido en los números complejos. En este caso, el discriminante se anula si y solo si el polinomio tiene raíces múltiples en su cuerpo de descomposición.El concepto de discriminante ha sido generalizado a otras estructuras algebraicas además de los polinomios, incluyendo secciones cónicas, formas cuadráticas y cuerpos de números algebraicos. Los discriminantes en la teoría de números algebraicos están fuertemente relacionados y contienen información sobre ramificaciones. De hecho, los tipos de ramificación están relacionados con tipos más abstractos de discriminantes, lo que convierte esta idea algebraica en capital en muchas aplicaciones. El discriminante de un polinomio
El discriminante de los polinomios cuadráticos
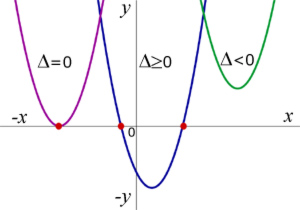
El polinomio cuadrático P(x) = ax2 + bx + c tiene discriminante D = b2 − 4ac, que es la cantidad bajo el signo de la raíz cuadrada en la fórmula de la solución de la ecuación de segundo grado. Dados los números reales a, b, c, se tiene:- Cuando D > 0, P(x) tiene dos raíces reales distintas , y su representación cruza el eje de las abscisas dos veces.
- Cuando D = 0, P(x) tiene dos raíces coincidentes reales , y su representación es tangente al eje de abscisas.
- Cuando D < 0, P(x) no tiene raíces reales y su representación queda estrictamente por encima o por debajo del eje de abscisas. En este caso, P(x) tiene dos raíces complejas distintas.
El discriminante de los polinomios cúbicos
El polinomio cúbico- tiene discriminante .
Los polinomios más simples tienen discriminantes con expresiones más simples. Por ejemplo el polinomio mónico cuadrático- tiene discriminante .
el polinomio mónico cúbico- tiene discriminante .
El polinomio mónico cúbico sin término cuadrático- tiene discriminante .
Caso general
El discriminante del polinomio generales, hasta cierto factor, igual al determinante de la matriz (2n − 1)×(2n − 1) (Véase también: matriz de Sylvester)
El determinante de esta matriz se conoce como la resultante de y , notación . El discriminante de viene dado por- .
PorEl discriminante del polinomio de cuarto grado se obtiene a partir de su determinante dividiéndolo por .
De forma equivalente, el discriminante es igual adonde r1,..., rn son las raíces complejas (contando su multiplicidad) del polinomio p(x):Esta segunda expresión clarifica que p tiene raíz múltiple si y solo si el discriminante es cero (la raíz múltiple puede ser compleja).El discriminante puede definirse para polinomios en cuerpos arbitrarios de la misma manera. La fórmula que involucra las raíces ri igue siendo válida; las raíces tienen que tomarse en un cuerpo de descomposición del polinomio.Discriminante de una sección cónica
Para una sección cónica definida por el polinomio real:- ax2 + bxy + cy2 + dx + ey + f= 0,
el discriminante es igual a- b2 − 4ac,
y determina la forma de la sección cónica. Si el discriminante es menor a 0, la ecuación describe una elipse o una circunferencia. Si el discriminante es igual a 0, la ecuación describe una parábola. Si por el contrario es mayor a cero, la ecuación describe una hipérbola. Esta fórmula no funciona en los casos en que el polinomio ya se ha factorizado.Discriminante de una forma cuadrática
Hay una generalización de las formas cuadráticas Q sobre cualquier cuerpo K de característica ≠ 2. Pueden expresarse como la suma de términos- aiLi2
donde los términos Li son formas lineales y 1 ≤ i ≤ n donde n es el número de variables. Entonces el discriminante es el producto de ai, tomado en K/K2, y está bien definido. Una forma más invariante de decir lo mismo es que es el determinante de una matriz simétrica para Q.Ecuaciones cuadráticas ¿qué es el discriminante?
Presta atención a la siguiente imagen, en donde te mostramos la forma tipo de una ecuación cuadrática completa y la fórmula para resolverla de la que hablábamos antes.Ahora bien, el discriminante, precisamente es una parte de esta fórmula, pero una parte realmente muy importante ya que nos permitirá (si lo estudiamos por separado) determinar cuántas y qué tipo de soluciones tendrá la ecuación cuadrática en cuestión. De allí su nombre…, porque si lo piensas lo que nos permite en definitiva es discriminar.Pero vamos por partes… ¿a qué parte de esta fórmula llamamos exactamente discriminante? La siguiente imagen te lo muestra claramente:Se llama discriminante a la parte que está afectada por la raíz cuadrada, que, en la imagen anterior está destacada en color rojo.¿Para qué nos sirve analizar el discriminante? Porque de su análisis sólo podrán surgir tres casos y en consecuencia, habrá sólo tres tipos de raíces o soluciones. El detalle consta en la siguiente imagen:El discriminante se simboliza con la letra griega Delta, por lo que con frecuencia encontrarás expresiones como la que sigue, cuando se hace referencia al estudio de un discriminante:Esto mismo, expresado desde el punto de vista de la gráfica de la ecuación cuadrática (es decir cuando se convierte en función), se visualiza mucho mejor; presta atenciónEn resumen, hemos respondido a la pregunta inicial: ya sabemos qué es el discriminante y para qué se usa. Te aseguro que es una herramienta muy potente a la hora de realizar el estudio de funciones más avanzadas y complejas, con las que seguramente te encontrarás en cursos superiores.- http://matematicasmodernas.com/ecuaciones-cuadraticas-que-es-el-discriminante/


















































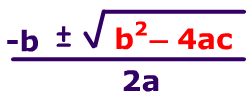


No hay comentarios:
Publicar un comentario