forma indeterminada a una expresión algebraica que involucra límites del tipo:
 .
.
Estas expresiones se encuentran con frecuencia dentro del contexto del límite de funciones y, más generalmente, del cálculo infinitesimal y el análisis real.
Interpretación
El hecho de que dos funciones f y g se acerquen ambas a cero cuando x tiende a algún punto de acumulación c no es información suficiente para evaluar el límite
Dicho límite puede converger a cualquier valor, puede converger a infinito o puede no existir, dependiendo de las funciones f y g.
Cociente indeterminado
La forma 0/0
Un ejemplo muy frecuente es la forma indeterminada del tipo 0/0. Cuando x se acerca a 0, las razones x/x3, x/x, y x2/x se van a 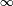 , 1, y 0 respectivamente. En cada caso, sin embargo, si los límites del numerador y del denominador se evalúan en la operación de división, el resultado es 0/0. De manera que (hablando informalmente) 0/0 puede ser 0,
, 1, y 0 respectivamente. En cada caso, sin embargo, si los límites del numerador y del denominador se evalúan en la operación de división, el resultado es 0/0. De manera que (hablando informalmente) 0/0 puede ser 0, 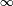 o incluso 1 y, de hecho, es posible construir otros ejemplos similares que converjan a cualquier valor particular. Por ello es que la expresión 0/0 se dice que es indeterminada.
o incluso 1 y, de hecho, es posible construir otros ejemplos similares que converjan a cualquier valor particular. Por ello es que la expresión 0/0 se dice que es indeterminada.
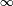 , 1, y 0 respectivamente. En cada caso, sin embargo, si los límites del numerador y del denominador se evalúan en la operación de división, el resultado es 0/0. De manera que (hablando informalmente) 0/0 puede ser 0,
, 1, y 0 respectivamente. En cada caso, sin embargo, si los límites del numerador y del denominador se evalúan en la operación de división, el resultado es 0/0. De manera que (hablando informalmente) 0/0 puede ser 0, 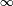 o incluso 1 y, de hecho, es posible construir otros ejemplos similares que converjan a cualquier valor particular. Por ello es que la expresión 0/0 se dice que es indeterminada.
o incluso 1 y, de hecho, es posible construir otros ejemplos similares que converjan a cualquier valor particular. Por ello es que la expresión 0/0 se dice que es indeterminada.
Ejemplos:
La forma ∞/∞
Esta forma indeterminada se da en cocientes en los cuales, tanto el numerador como el denominador, tienen por límite ∞. En estos casos, no se puede aplicar ningunaregla operatoria, por lo que se dice que se está frente a una forma indeterminada del tipo ∞/∞. Para resolver esta indeterminación pueden aplicarse métodos tales como factorización, derivación, el teorema del emparedado, entre otros.
Ejemplos:
Producto indeterminado
La forma indeterminada 0 • ∞
Diferencia indeterminada
En los casos en que el límite de una diferencia es  , no se puede aplicar ninguna regla operatoria para límites, por lo que se dice que se está frente a una forma ideterminada del tipo
, no se puede aplicar ninguna regla operatoria para límites, por lo que se dice que se está frente a una forma ideterminada del tipo 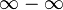 . Para resolver esta indeterminación pueden aplicarse métodos como la multiplicación por los polinomios conjugados.
. Para resolver esta indeterminación pueden aplicarse métodos como la multiplicación por los polinomios conjugados.
 , no se puede aplicar ninguna regla operatoria para límites, por lo que se dice que se está frente a una forma ideterminada del tipo
, no se puede aplicar ninguna regla operatoria para límites, por lo que se dice que se está frente a una forma ideterminada del tipo 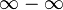 . Para resolver esta indeterminación pueden aplicarse métodos como la multiplicación por los polinomios conjugados.
. Para resolver esta indeterminación pueden aplicarse métodos como la multiplicación por los polinomios conjugados.Potencia indeterminada
- La forma 00
- La forma ∞0
- La forma 1∞
Ejemplo: el siguiente límite1
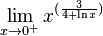 , es de la forma
, es de la forma  ; considerando
; considerando
y tomando logaritmos en ambos miembros resulta
 aplicando al segundo miembro la regla de l'Hôpital, se obtiene
aplicando al segundo miembro la regla de l'Hôpital, se obtiene
 de manera que el límite sería
de manera que el límite sería
Tabla de formas indeterminadas
La siguiente tabla contiene las formas indeterminadas y las transformaciones bajo la regla de l'Hôpital.
| Forma indeterminada | Condiciones | Transformación a 0/0 | Transformación a ∞/∞ |
|---|---|---|---|
 |  | 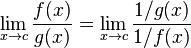 | |
 | 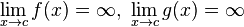 | 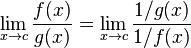 | |
 | 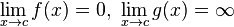 | 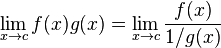 | 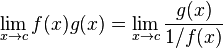 |
 | 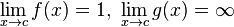 |  | 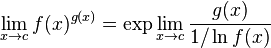 |
 |  | 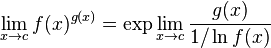 |  |
 |  | 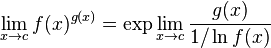 |  |
 | 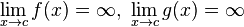 | 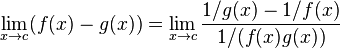 |  |
Límites indeterminados
Se llaman límites indeterminados a los que presentan alguna de estas formas:
Contra lo que se pudiera pensar, un límite de la forma ¥ - ¥ no da, en general, como resultado cero, tampoco un límite de la forma 1¥ da siempre como resultado uno. Por esta razón se les llama límites indeterminados y se requiere hacer un estudio particular para cada caso.
Obsérvese que ya se han estudiado varios casos de indeterminaciones de la
-¥ a +¥ pasando por todos los valores intermedios.
Ejemplo:
Resolución:
·Este límite es de la forma ¥ - ¥. Indeterminado.
Este límite se resuelve multiplicando y dividiendo por el conjugado, es decir, por
· Por tanto el límite se reduce a calcular
Resolución:
· El primer factor tiene por límite cero ya que el grado del numerador es menor que el del denominador.
· El segundo factor tiene por límite ¥ pues el grado del numerador es mayor que el del denominador.
· El límite es por tanto de la forma 0·¥ . Indeterminado.
· Multiplicando las dos fracciones:
· Al ser un cociente de polinomios de igual grado,
Resolución:
Resolución:
·Se saca factor común n2 en la expresión n2 + 3n -2:
Las formas de Chern-Simons, en matemáticas, son ciertas clases características secundarias. Se les han encontrado interés en teoría de gauge, y (especialmente las 3-formas) definen la acción de la teoría de Chern-Simons. El nombre se debe a sus creadores, Shiing-Shen Chern y Jim Simons.
Dado una variedad y una 1-forma A a valores en un álgebra de Lie, se puede definir una familia de p-formas:
En una dimensión, la 1-forma de Chern-Simons viene dada por
En tres dimensiones, las 3-formas de Chern-Simons vienen dadas por
En cinco dimensiones, las 5-formas de Chern-Simons vienen dadas por
donde se define la curvatura F como
La forma general de Chern-Simons ω2k-1 se define de manera tal que dω2k-1 = Tr (Fk) donde se utiliza para definir Fk el producto cuña.
Véase teoría de gauge para más detalles.
En general, la p-forma de Chern-Simons se define para cualquier p impar. Confrontar teoría de gauge para las definiciones. Su integral sobre una variedad p-dimensional es un invariante de homotopía. Este valor se llama el número de Chern.
función analítica es aquella que puede expresarse como una serie de potencias convergente. Una función analítica es suave si tiene infinitas derivadas. La noción de función analítica puede definirse para funciones reales o complejas, aunque ambos conjuntos tienen propiedades distintas. Las funcionescomplejas derivables en un abierto siempre son analíticas, y se denominan funciones holomorfas. Sin embargo, una función real infinitamente derivable no es necesariamente analítica.
La definición de función analítica es idéntica para los casos real y complejo:
De esta definición se puede demostrar la siguiente caracterización alternativa:
Una función se dice analítica en un conjunto U si es analítica en cada punto de U. El conjunto de todas las funciones analíticas en un cierto abierto U se denota porCω(U).
Varias variables
La definición de función analítica puede extenderse para funciones (reales o complejas) de varias variables (definidas en Rn o Cn), sin más que considerar series de potencias de varias variables:
Funciones holomorfas
En el caso de las funciones complejas analíticas, existe un teorema que las caracteriza de manera mucho más sencilla, y que constituye uno de los rasgos fundamentales del análisis complejo:
Un teorema similar se aplica en el caso de funciones complejas de varias variables que sean diferenciables:
Funciones suaves no analíticas
En variable real pueden encontrarse funciones suaves que no son analíticas. Un ejemplo de ello es la función:
Esta función es infinitamente derivable para cualquier x ∈ R, y en particular todas sus derivadas en 0 son nulas: f(n)(0) = 0. Por tanto, su serie de Taylor alrededor de 0 es identicamente nula, y en ningún entorno de dicho punto coinciden la función y la serie de Taylor.
las funciones analíticas .- .....................................:http://www.dmae.upm.es/WebpersonalBartolo/VariableCompleja/VCParteI/3_Funciones_Analiticas.pdf
las funciones analíticas .- ........................................:https://es.wikipedia.org/w/index.php?title=Funci%C3%B3n_anal%C3%ADtica&printable=yes
|
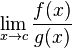

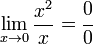

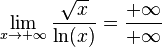
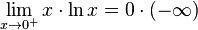
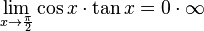



![Tr[\bold{A}]](https://upload.wikimedia.org/math/9/5/9/9597cba36d9b8f9cd4e1ada5634d7419.png) .
.![Tr[\bold{F}\wedge\bold{A}-\frac{1}{3}\bold{A}\wedge\bold{A}\wedge\bold{A}]](https://upload.wikimedia.org/math/5/a/b/5ab69450f31b7dc014167e0d7b4bf082.png) .
.![Tr[\bold{F}\wedge\bold{F}\wedge\bold{A}-\frac{1}{2}\bold{F}\wedge\bold{A}\wedge\bold{A}\wedge\bold{A} +\frac{1}{10}\bold{A}\wedge\bold{A}\wedge\bold{A}\wedge\bold{A}\wedge\bold{A}]](https://upload.wikimedia.org/math/5/0/f/50fb5bceba4d4ebe3f41fc5cf8bfa193.png)
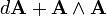 .
.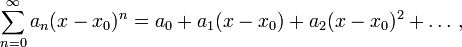
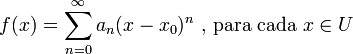


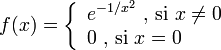
No hay comentarios:
Publicar un comentario