entorno (o
vecindad[cita requerida]) es uno de los conceptos básicos de los
espacios topológicos. Intuitivamente hablando, un entorno de un punto es un conjunto que contiene al punto en donde uno puede separarse un poco del punto en cuestión sin abandonar el conjunto.
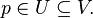
Nótese que el entorno V no necesita ser un conjunto abierto. Si V es abierto se lo llama un entorno abierto. Algunos autores especifican que los entornos deben ser abiertos, por lo que es importante prestar cuidado a las diferentes notaciones.
El conjunto de todos los entornos de un punto forma una
base de entornos del punto.
Si
S es un
subconjunto de
X, un entorno de
S es un conjunto
V, que contiene un conjunto abierto
U que contiene a
S. Se deduce que un conjunto
V es un entorno de
S si y solo si es un entorno de todos los puntos de
S.
Clases de entorno
- Entorno reducido: un entorno
 de un punto
de un punto  es un entorno reducido si el propio punto
es un entorno reducido si el propio punto  no pertenece al mismo. Es decir, está compuesto solamente por los puntos cercanos a
no pertenece al mismo. Es decir, está compuesto solamente por los puntos cercanos a 
- Entornos abiertos: un entorno
 de un punto
de un punto  es entorno abierto de
es entorno abierto de  si
si  es un conjunto abierto (es decir,
es un conjunto abierto (es decir,  ).
).
- Entornos cerrados: un entorno
 de un punto
de un punto  es entorno cerrado de
es entorno cerrado de  si
si  es un conjunto cerrado.
es un conjunto cerrado.
- Entorno compacto: un entorno
 de un punto
de un punto  es entorno compacto de
es entorno compacto de  si
si  es un conjunto compacto.
es un conjunto compacto.
- Entorno conexo: un entorno
 de un punto
de un punto  es entorno conexo de
es entorno conexo de  si
si  es un conjunto conexo
es un conjunto conexo
- Entorno conexo por caminos: un entorno
 de un punto
de un punto  es entorno conexo por caminos de
es entorno conexo por caminos de  si
si  es un conjunto conexo por caminos.
es un conjunto conexo por caminos.
- Entorno simplemente conexo: un entorno
 de un punto
de un punto  es entorno simplemente conexo de
es entorno simplemente conexo de  si
si  es un conjunto simplemente conexo.
es un conjunto simplemente conexo.
- Entorno convexo: un entorno
 de un punto
de un punto  en un espacio vectorial topológico
en un espacio vectorial topológico  es entorno convexo de
es entorno convexo de  si
si  es un conjunto convexo.
es un conjunto convexo.
En el espacio métrico

Un conjunto

en el plano y un entorno uniforme

de

.

que es contenida en V.
V es llamado entorno uniforme de un conjunto S si existe un número positivo r tal que para todos los elementos p de S,

estén contenidos en V.
Para
r>0 el
r-entorno 
de un conjunto
S es el conjunto de todos los puntos en
X que distan menos de
r desde
S (o equivalentemente,

es la unión de todas las bolas abiertas de radio
r que tienen centro en un punto de
S).
Se deduce entonces que un r-entorno es un entorno uniforme, y que un conjunto es un entorno uniforme si y solo si contiene un r-entorno para algún valor de r.
Ejemplo

Entorno de centro a y radio ε.
entonces
V es un entorno del conjunto

de
números naturales, pero no es un entorno uniforme de este conjunto.
Topología de entornos
La definición superior es útil si la noción de
conjunto abierto está previamente definida. Existe una forma alternativa de definir una topología, primeramente definiendo su
base de entornos, y entonces los conjuntos abiertos como aquellos conjuntos que contienen un entorno para cada uno de sus puntos.
Una base de entornos en
X es la asignación de un
filtro N(x) (en el conjunto
X) para cada
x en
X tal que:
- el punto x es un elemento de cada U en N(x).
- cada U en N(x) contiene algún V en N(x) tal que para cada y en V, U esté en N(y).
Entorno uniforme
En un
espacio uniforme S:=(
X, δ)
V es denominado
entorno uniforme de
P si
P no es cercano a
X \
V, tal que allí no exista un espacio uniforme que contenga a
P y
X \
V.
Entorno reducido
Un
entorno reducido de un punto
p es un entorno de
p, menos {
p}. Por ejemplo, el
intervalo (−1, 1) = {
y : −1 <
y < 1} es un entorno de
p = 0 en la
recta real, entonces el conjunto (−1, 0) ∪ (0, 1) = (−1, 1) − {0} es un entorno
reducido de 0.
Definición de entorno
Se llama entorno de centro a y radio r, y se denota por Er(a) o E(a,r), al intervalo abierto (a-r, a+r).
Er(a) = (a-r, a+r)
Los entornos se expresan con ayuda del valor absoluto.
Er(0) = (-r, r) se expresa también |x|, o bien, -r < x < r.
Entornos laterales
1 Por la izquierda
Er(a-) = (a-r, a]
1 Por la derecha
Er(a+) = [a, a+r)
Entorno reducido
Se emplea cuando se quiere saber qué pasa en las proximidades del punto, sin que interese lo que ocurre en dicho punto.
E r*(a) = { x  (a-r, a+r), x ≠ a}
(a-r, a+r), x ≠ a}
Una función como
en la
recta real 
, no es de
cuadrado integrable para la medida de Borel usual en

. Claramente la función exponencial compleja pertenece al espacio vectorial complejo

(que no es un espacio de Hilbert) pero no pertenece al espacio de Hilbert
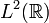
(asociado a la medida de Lebesgue-Borel).
Para poder definir propiedades de
ortogonalidad a la función exponencial compleja del ejemplo anterior, se requiere un marco que exceda los límites estrictos de la teoría del
espacio de Hilbert. Esto fue provisto por el aparato de
distribuciones de Schwartz, y la teoría generalizada de la función propia fue desarrollada en los años 1950.
Introducción
El concepto del espacio equipado de Hilbert pone esta idea en marco funcional-analítico abstracto. Formalmente, un espacio equipado de Hilbert consiste en el
espacio de Hilbert H, junto con un subespacio Φ que lleva una topología más fina, para la cual la inclusión natural o
inyección canónica:
es continua. Se puede asumir que ese Φ es
denso en
H para la norma de Hilbert. Consideramos la inclusión del
espacio dual H* en Φ
*. El último, dual al Φ en su topología de la función de prueba, se realiza como un espacio de distribuciones o de funciones generalizadas de una cierta clase, y los funcionales lineales en el subespacio Φ del tipo:
para
v en
H se representan fielmente como distribuciones (porque asumimos Φ denso). Ahora aplicando el
teorema de representación de Riesz podemos identificar
H*con
H. Por lo tanto la definición del
espacio equipado de Hilbert es en términos de un sándwich
Definición formal
Un espacio de Hilbert equipado es una tripleta

donde el par
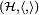
constituye un espacio de Hilbert ordinario y el conjunto

es un espacio vectorial
denso en el espacio

y no reflexivo (

) tal que

. Como condición adicional se exigen que

puede ser continuamente encajado en el espacio

, es decir, que la que
inyección canónica i sea continua:
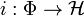
.
Dado que

, por ser todo espacio de Hilbert reflexivo, el operador adjunto dado por:
También debe ser una aplicación continua. La dualidad entre

y

también debe ser compatible con el producto de

, en el sentido de que:
para cualesquiera

y
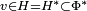
La tripleta

se denomina frecuentemente "terna de Gelfand" (en honor al matemático
Izrail Gélfand). Nótese que aunque

es isomorfo a

en el que caso de que

sea en sí mismo un espacio de Hilbert, este isomorfismo
no es el mismo que la composición de la inyección canónica
i con su adjunto
i*
EHE en Mecánica cuántica
En
mecánica cuántica el formalismo de espacios de Hilbert equipados permite tratar de un modo similar los
estados ligados de partículas y estados libres (idealizados, o de colisión). Un estado ligado corresponde normalmente a una situación donde una partícula tiene su movimiento restringido a una región finita del espacio, mientras que en un estado libre, más pertinentemente no-ligado, la partícula puede moverse por todo el espacio. Los estados ligados pueden representarse por vectores ordinarios en un espacio de Hilbert de tipo
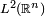
, mientras que los estados no-ligados al representar partículas cuyo movimiento no se restringe a una función comparte deberán ser modelizados por funciones en general no integrables y que no pertenecen al espacio de Hilbert de funciones de cuadrado integrable.
Un ejemplo físico aclara la situación. Si consideramos un
átomo de hidrógeno los estados ligados corresponden a los electrones que orbitan alrededor del núcleo y no van mucho más allá del radio atómico, en este caso su
energía mecánica total es negativa. Por otro lado un estado libre correspondería a la situación de un electrón con energía positiva se acerca al núcleo del átomo interactúa con él siendo desviado de su trayectoria pero tiene suficiente energía como para no ser capturado por el núcleo continuando así su camino lejos del átomo.
Desde un punto de vista matemático los estados ligados son
vectores propios del
Hamiltoniano (asociado a valores del espectro puntual del mismo). Por el contrario el
espectro continuo del Hamiltoniano, que correspondería a estados libres carece de vectores propios propiamente dichos en un espacio de Hilbert convencional. Si se amplía el espacio de Hilbert convencional con ciertos vectores adicionales, entonces ciertos estados libres físicamente razonables pueden ser tratados como vectores propios generalizados correspondientes al espectro continuo.
Este tipo de espacios se nombra así en honor a
Laurent Schwartz. Una función del espacio de space se llama a veces
función de Schwartz.
El espacio de Schwartz o
espacio de funciones de decrecimiento rápido 
definido sobre el
espacio euclídeo 
es el conjunto de funciones:
Donde:
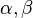 son multíndices (conjuntos ordenados de índices).
son multíndices (conjuntos ordenados de índices). es el conjunto de funciones reales suaves sobre
es el conjunto de funciones reales suaves sobre  .
. es una norma definida a partir de la norma del supremo como:
es una norma definida a partir de la norma del supremo como:
Donde los números
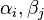
son enteros positivos que satisfacen:
Ejemplos de funciones en 
Propiedades
 es un espacio de Fréchet sobre los números complejos
es un espacio de Fréchet sobre los números complejos  .
.- Por la regla de Leibniz se sigue que
 es cerrado bajo la multiplicación punto a punto, es decir,
es cerrado bajo la multiplicación punto a punto, es decir,  .
.
- La tansformada de Fourier es un automorfismo lineal acotado de
 en sí mismo.
en sí mismo.
- Para cualquier
 , se tiene que
, se tiene que 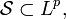 donde Lp(Rn) es el espacio de funciones p-integrables en Rn. En particular, cualquier función de
donde Lp(Rn) es el espacio de funciones p-integrables en Rn. En particular, cualquier función de  es una función acotada.
es una función acotada.

Una
función gausiana bidimensional es un ejemplo de función de decrecimiento rápido, y por tanto, un elemento del espacio de Schwartz.
 de un punto
de un punto  es un entorno reducido si el propio punto
es un entorno reducido si el propio punto  no pertenece al mismo. Es decir, está compuesto solamente por los puntos cercanos a
no pertenece al mismo. Es decir, está compuesto solamente por los puntos cercanos a 
 de un punto
de un punto  es entorno abierto de
es entorno abierto de  si
si  es un conjunto abierto (es decir,
es un conjunto abierto (es decir,  ).
). de un punto
de un punto  es entorno cerrado de
es entorno cerrado de  si
si  es un conjunto cerrado.
es un conjunto cerrado. de un punto
de un punto  es entorno compacto de
es entorno compacto de  si
si  es un conjunto compacto.
es un conjunto compacto. de un punto
de un punto  es entorno conexo de
es entorno conexo de  si
si  es un conjunto conexo
es un conjunto conexo de un punto
de un punto  es entorno conexo por caminos de
es entorno conexo por caminos de  si
si  es un conjunto conexo por caminos.
es un conjunto conexo por caminos. de un punto
de un punto  es entorno simplemente conexo de
es entorno simplemente conexo de  si
si  es un conjunto simplemente conexo.
es un conjunto simplemente conexo. de un punto
de un punto  en un espacio vectorial topológico
en un espacio vectorial topológico  es entorno convexo de
es entorno convexo de  si
si  es un conjunto convexo.
es un conjunto convexo. de un conjunto S es el conjunto de todos los puntos en X que distan menos de r desde S (o equivalentemente,
de un conjunto S es el conjunto de todos los puntos en X que distan menos de r desde S (o equivalentemente,  es la unión de todas las bolas abiertas de radio r que tienen centro en un punto de S).
es la unión de todas las bolas abiertas de radio r que tienen centro en un punto de S). de un conjunto S es el conjunto de todos los puntos en X que distan menos de r desde S (o equivalentemente,
de un conjunto S es el conjunto de todos los puntos en X que distan menos de r desde S (o equivalentemente,  es la unión de todas las bolas abiertas de radio r que tienen centro en un punto de S).
es la unión de todas las bolas abiertas de radio r que tienen centro en un punto de S). de números naturales, pero no es un entorno uniforme de este conjunto.
de números naturales, pero no es un entorno uniforme de este conjunto. de números naturales, pero no es un entorno uniforme de este conjunto.
de números naturales, pero no es un entorno uniforme de este conjunto.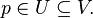

 en el plano y un entorno uniforme
en el plano y un entorno uniforme  .
.


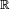 con la
con la 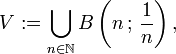
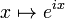
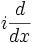
 , no es de
, no es de  (que no es un espacio de Hilbert) pero no pertenece al espacio de Hilbert
(que no es un espacio de Hilbert) pero no pertenece al espacio de Hilbert 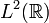 (asociado a la medida de Lebesgue-Borel).
(asociado a la medida de Lebesgue-Borel).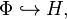
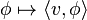

 donde el par
donde el par 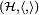 constituye un espacio de Hilbert ordinario y el conjunto
constituye un espacio de Hilbert ordinario y el conjunto  es un espacio vectorial
es un espacio vectorial  y no reflexivo (
y no reflexivo ( ) tal que
) tal que  . Como condición adicional se exigen que
. Como condición adicional se exigen que 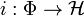 .
. , por ser todo espacio de Hilbert reflexivo, el operador adjunto dado por:
, por ser todo espacio de Hilbert reflexivo, el operador adjunto dado por: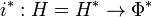
 también debe ser compatible con el producto de
también debe ser compatible con el producto de 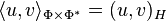
 y
y 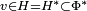
 se denomina frecuentemente "terna de Gelfand" (en honor al matemático
se denomina frecuentemente "terna de Gelfand" (en honor al matemático  en el que caso de que
en el que caso de que 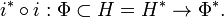
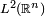 , mientras que los estados no-ligados al representar partículas cuyo movimiento no se restringe a una función comparte deberán ser modelizados por funciones en general no integrables y que no pertenecen al espacio de Hilbert de funciones de cuadrado integrable.
, mientras que los estados no-ligados al representar partículas cuyo movimiento no se restringe a una función comparte deberán ser modelizados por funciones en general no integrables y que no pertenecen al espacio de Hilbert de funciones de cuadrado integrable. del espacio de Schwartz.
del espacio de Schwartz. definido sobre el
definido sobre el  es el conjunto de funciones:
es el conjunto de funciones: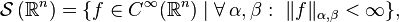
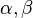 son multíndices (conjuntos ordenados de índices).
son multíndices (conjuntos ordenados de índices). es el conjunto de funciones reales suaves sobre
es el conjunto de funciones reales suaves sobre  es una
es una 
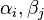 son enteros positivos que satisfacen:
son enteros positivos que satisfacen: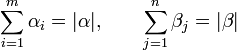
 , entonces
, entonces  .
. .
. .
. , se tiene que
, se tiene que 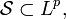 donde Lp(Rn) es el espacio de
donde Lp(Rn) es el espacio de 
No hay comentarios:
Publicar un comentario