Dentro de la amplia variedad de funciones matemáticas existentes se encuentran algunas que presentan comportamientos extraños e inesperados cuando se le asignan determinados valores a la/s variable/s independiente/s. Dicho comportamiento se describe con el nombre de singularidad de la función.
Concepto intuitivo de continuidad
Intuitivamente se asocia la idea de continuidad de una función al hecho de no levantar el lápiz cuando se representa la función. Las discontinuidades generalmente se clasifican en varios tipos, siendo las llamadas de salto uno de los tipos más frecuentes. Dentro de dicho tipo existen las discontinuidades de salto puntuales, en las que la función se desvía un único punto del camino más razonable; las discontinuidades de salto finito, en las cuales la función salta un valor y prosigue de forma continua a partir de ahí; y por último las discontinuidades de salto infinito, en las que la función alcanza un valor infinito. Estas últimas son las que reciben el nombre desingularidades.
Criterio de análisis de continuidad en funciones de una variable:
Una función  es continua en
es continua en  si y sólo si:
si y sólo si:
 es continua en
es continua en  si y sólo si:
si y sólo si: está definido.
está definido.- Existe el límite de
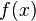 cuando
cuando  tiende a
tiende a  .
. - El límite de
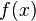 cuando
cuando  tiende a
tiende a  coincide con
coincide con  .
.
Funciones singulares
Existe una gran variedad de funciones elementales que contienen singularidades en sus dominios. Una de las más comunes suele ser la hipérbola elemental  . Esta función posee una singularidad en el punto
. Esta función posee una singularidad en el punto 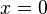 , en dicho punto la función presenta un comportamiento asintótico que tiende al infinito. Dicha función pone de manifiesto la carácterística de que toda función racional cuyo denominador se anule presentará una singularidad en el punto en el que eso suceda. así pues la función
, en dicho punto la función presenta un comportamiento asintótico que tiende al infinito. Dicha función pone de manifiesto la carácterística de que toda función racional cuyo denominador se anule presentará una singularidad en el punto en el que eso suceda. así pues la función  presentará una singularidad en el punto
presentará una singularidad en el punto 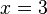 . Otras funciones que contienen singularidades son
. Otras funciones que contienen singularidades son  ó
ó  .
.
 . Esta función posee una singularidad en el punto
. Esta función posee una singularidad en el punto 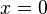 , en dicho punto la función presenta un comportamiento asintótico que tiende al infinito. Dicha función pone de manifiesto la carácterística de que toda función racional cuyo denominador se anule presentará una singularidad en el punto en el que eso suceda. así pues la función
, en dicho punto la función presenta un comportamiento asintótico que tiende al infinito. Dicha función pone de manifiesto la carácterística de que toda función racional cuyo denominador se anule presentará una singularidad en el punto en el que eso suceda. así pues la función  presentará una singularidad en el punto
presentará una singularidad en el punto 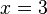 . Otras funciones que contienen singularidades son
. Otras funciones que contienen singularidades son  ó
ó  .
.Análisis de las singularidades
Normalmente las singularidades no pueden estudiarse empleando técnicas aritméticas elementales, ya que suelen implicar operaciones que son imposibles de realizar (por ejemplo, dividir por cero). En lugar de eso, el método preferido para analizar el comportamiento de las funciones en sus singularidades es el paso al límite. Estudiando el límite de una función en su punto singular se puede obtener información valiosa de su comportamiento en ese punto. Como ejemplo comentar que nadie puede calcular que  toma en el punto
toma en el punto 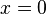 el valor infinito, sin embargo, estudiando el valor que toma su límite en ese punto y analizando la tendencia de la función en las cercanías es posible asegurarlo.
el valor infinito, sin embargo, estudiando el valor que toma su límite en ese punto y analizando la tendencia de la función en las cercanías es posible asegurarlo.
 toma en el punto
toma en el punto 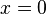 el valor infinito, sin embargo, estudiando el valor que toma su límite en ese punto y analizando la tendencia de la función en las cercanías es posible asegurarlo.
el valor infinito, sin embargo, estudiando el valor que toma su límite en ese punto y analizando la tendencia de la función en las cercanías es posible asegurarlo.Singularidades en variable compleja
Además, si  es una singularidad de
es una singularidad de 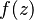 , decimos que es una singularidad no aislada si
, decimos que es una singularidad no aislada si
 es una singularidad de
es una singularidad de 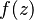 , decimos que es una singularidad no aislada si
, decimos que es una singularidad no aislada sies singular en
.
Es decir, a una distancia arbitraria, se encuentra otra singularidad.
 es una singularidad aislada si no cumple con lo expresado anteriormente. Esto significa que puede tomarse cierta distancia alredeor del punto
es una singularidad aislada si no cumple con lo expresado anteriormente. Esto significa que puede tomarse cierta distancia alredeor del punto  en la cual este punto es la única singularidad.
en la cual este punto es la única singularidad.
Las singularidades aisladas pueden clasificarse en:
- Evitables: Puede definirse un valor tal que
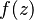 sea analítica en
sea analítica en  .
.
- Polares:
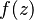 tiende a
tiende a  al acercarse a
al acercarse a  .
.
- Esenciales: El límite no existe, y aún más, la función toma valores por todo el plano complejo (excepto uno) en un entorno a
 y lo hace infinitas veces.
y lo hace infinitas veces.
Es posible estudiar el tipo de singularidad aislada, mediante el desarrollo de Laurent en la corona centrada en  . Si la serie principal (la de potencias negativas) tiene finitos términos, se trata de una singularidad polar, caso contrario, es esencial. Lógicamente se desprende, que si el desarrollo de Laurent se reduce a una serie de Taylor, la singularidad es evitable.
. Si la serie principal (la de potencias negativas) tiene finitos términos, se trata de una singularidad polar, caso contrario, es esencial. Lógicamente se desprende, que si el desarrollo de Laurent se reduce a una serie de Taylor, la singularidad es evitable.
 . Si la serie principal (la de potencias negativas) tiene finitos términos, se trata de una singularidad polar, caso contrario, es esencial. Lógicamente se desprende, que si el desarrollo de Laurent se reduce a una serie de Taylor, la singularidad es evitable.
. Si la serie principal (la de potencias negativas) tiene finitos términos, se trata de una singularidad polar, caso contrario, es esencial. Lógicamente se desprende, que si el desarrollo de Laurent se reduce a una serie de Taylor, la singularidad es evitable.Interpretación física de las singularidades
El estudio de las singularidades desde el punto de vista matemático se limita específicamente a resolver el problema de la función que no está definida en el punto de estudio. Teorías tales como el electromagnetismo clásico de Maxwell contienen singularidades en sus ecuaciones básicas. En la teoría de Maxwell una de las singularidades más conocidas es la que predice un campo eléctrico infinito en el lugar donde se encuentra colocada una carga puntual.
Una de las singularidades más famosas de la física es la que se encuentra en la solución de Schwarzschild de las ecuaciones de campo de la relatividad general, singularidad en el continuo espacio-tiempo que predice la existencia de agujeros negros.
Actualmente uno de los campos de discusión abiertos más apasionante de la física es aquel que pretende estudiar si hubo o no singularidad en el principio del universo y si la habrá en el final del mismo.
sistema iterativo de funciones (SIF o IFS acrónimo del inglés Iterated function system) es una construcción matemática usada para representar de manera simple ciertos conjuntos fractales que presenten autosimilaridad. Muchos fractales clásicos autosimilares, autoafines y autoconformes pueden representarse como el único conjunto compacto invariante por un sistema iterativo de funciones contractivas.
Un sistema iterativo de funciones (SIF) sobre  (se puede generalizar a cualquier espacio métrico completo) se define a partir de un conjunto finito de contracciones
(se puede generalizar a cualquier espacio métrico completo) se define a partir de un conjunto finito de contracciones  con
con  . El carácter contractivo de estas funciones implica que:
. El carácter contractivo de estas funciones implica que:
 (se puede generalizar a cualquier espacio métrico completo) se define a partir de un conjunto finito de contracciones
(se puede generalizar a cualquier espacio métrico completo) se define a partir de un conjunto finito de contracciones  con
con  . El carácter contractivo de estas funciones implica que:
. El carácter contractivo de estas funciones implica que:
Si sobre un conjunto se aplican reiteradamente los anteriores aplicaciones contractivas (iterativamente), lo que resultará en un sistema iterativo de funciones (SIF).
Estas aplicaciones inducen una aplicación sobre el conjunto de partes del espaico métrico:
Una propiedad fundamental de los SIFs es que existe un "punto fijo" o que es un conjunto compacto E tal que:
Observamos que esta condición nos indica que el conjunto es igual a la unión de copias de sí mismo de menor tamaño. Por esa razón, frecuentemente ese conjunto es un conjunto fractal y su dimensión de Hausdorff D puede determinarse fácilmente, ya que es la única solución del sistema:
El conjunto de Cantor puede obtenerse como el "punto fijo" de un sistema iterativo de funciones. Dadas las dos funciones contractivas:
De hecho, el conjunto de Cantor es el único conjunto compacto tal que:
Y por tanto su dimensión fractal puede calcularse fácilmente:
Distancia de Hausdorff
Si consideran todos los conjuntos compactos  de un espacio topológico se puede definir un espacio métrico
de un espacio topológico se puede definir un espacio métrico  formado por dichos conjuntos y con la distancia de Hausdorff como función distancia de dicho espacio.
formado por dichos conjuntos y con la distancia de Hausdorff como función distancia de dicho espacio.
 de un espacio topológico se puede definir un espacio métrico
de un espacio topológico se puede definir un espacio métrico  formado por dichos conjuntos y con la distancia de Hausdorff como función distancia de dicho espacio.
formado por dichos conjuntos y con la distancia de Hausdorff como función distancia de dicho espacio.
Puede comprobarse que el espacio métrico  es un espacio completo. Todo sistema iterativo de funciones permite definir una contracción en el espacio métrico anterior:
es un espacio completo. Todo sistema iterativo de funciones permite definir una contracción en el espacio métrico anterior:
 es un espacio completo. Todo sistema iterativo de funciones permite definir una contracción en el espacio métrico anterior:
es un espacio completo. Todo sistema iterativo de funciones permite definir una contracción en el espacio métrico anterior:
Esta función es la restricción a conjuntos compactos de la contracción inducida por el SIF. Como toda contracción presenta un punto fijo, la aplicación anterior presenta un "punto fijo" o atractor, es decir, un conjunto compacto invariante por la aplicación anterior. El atractor o punto fijo de la aplicación anterior puede representarse como:
O equivalentemente como límite de la sucesión:
Dicho conjunto compacto usualmente es un conjunto fractal. La autosimilitud de K, una de las características de los fractales, se deriva de la condición de "punto fijo":
,
en la que observamos que K estará formado por unión de k copias de sí mismo, posiblemente deformadas, y de menor tamaño (si las aplicaciones son contractivas), que pueden solaparse o no.
Dimensión del atractor de un SIF
Todo SIF tiene un atractor, o conjunto compacto invariante por el SIF que frecuentemente es un objeto fractal. La dimensión de dicho atractor puede calcularse de manera sencilla si se satisface la condición del conjunto abierto (CCA), es decir, que exista un conjunto abierto no vacío  tal que:
tal que:
 tal que:
tal que:
Muchos fractales clásicos como la curva de Koch o la alfombra de Sierpiński satisfacen la CCA. Si las funciones del SIF son semejanzas, para el cálculo de la dimensión se tiene el siguiente teorema:
- Si
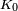 el atractor de una familia o SIF de semejanzas contractivas
el atractor de una familia o SIF de semejanzas contractivas  donde la constante de Lipschitz para
donde la constante de Lipschitz para  es
es  y si se satisface la condición de conjunto abierto CCA entonces se tiene la siguiente relación entre las dimensiones fractales (de Hausdorff-Besicovitch y Minkowski-Bouligand):
y si se satisface la condición de conjunto abierto CCA entonces se tiene la siguiente relación entre las dimensiones fractales (de Hausdorff-Besicovitch y Minkowski-Bouligand):
- siendo la medida de Hausdorff finita y no nula para esa dimensión, y además se cumple que:
Esta última expreisón permite calcular la dimensión fractal (D) del atractor del SIF compuesto de n aplicaciones contractivas de factor de contracción ri, en caso de que estas no provoquen solapamiento o más generalmente satisfagan la CCA.
El problema inverso: Teorema del collage
Este teorema nos permite encontrar un SIF cuyo atractor esté todo lo próximo que deseemos (en el sentido de la distancia de Hausdorff) o coincida con un conjunto prefijado C.
Para hallar dicho SIF necesitamos encontrar un número suficiente de aplicaciones contractivas tales que la unión (collage) de las imágenes del conjunto bajo estas aplicaciones esté lo suficientemente próxima o coincida con el propio conjunto.
Como ejemplo, para conseguir un SIF cuyo atractor corresponda al conjunto fractal de la figura son necesarias 3 transformaciones:
- La que lleva el conjunto total en el triángulo amarillo:
- La que lleva el conjunto total en el triángulo azul:
- La que lleva el conjunto total en el triángulo rojo:
Algoritmos de representación
Algoritmo determinista
Simplemente construye los sucesivos conjuntos {A, F(A), F(F(A)),...}. Como dicha sucesión converge al atractor del SIF independientemente del conjunto A de partida, puede usarse cualquier valor inicial, con frecuencia una caja cuadrada.
Algoritmo de iteración aleatoria
En este algoritmo, también llamado "juego del caos", un punto que describe una danza aparentemente aleatoria va perfilando progresivamente la estructura del atractor. Para ello, se elige un punto x0 del espacio métrico y se forma una sucesión del siguiente modo: en cada paso se escoge aleatoriamente y con igual probabilidad
Se demuestra que la sucesión así formada "converge" al atractor del SIF.
Este algoritmo permite una generalización en que se asignan distintas probabilidades pi a la hora de escoger cada fi. Diferentes probabilidades permiten obtener diversas texturas y densidades, útiles para el modelado de escenas naturales. Un SIF en que cada función fi va acompañada de un número positivo pi de modo que  se denomina SIF con probabilidades.
se denomina SIF con probabilidades.
 se denomina SIF con probabilidades.
se denomina SIF con probabilidades. , y una función
, y una función  se dice que
se dice que 




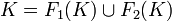











No hay comentarios:
Publicar un comentario