ecuación de Schröder,1 2 3 nombrada así en honor de Ernst Schröder, es una ecuación funcional con una variable independiente. Dada la función 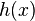 , la solución de la ecuación de Schröder es la función
, la solución de la ecuación de Schröder es la función 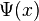 que cumple:
que cumple:
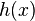 , la solución de la ecuación de Schröder es la función
, la solución de la ecuación de Schröder es la función 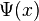 que cumple:
que cumple:
La ecuación de Schröder es un problema de autovalores para el operador de composición Ch, el cuál devuelve, para una función f(x), otra función f(h(x)).
Si a es un punto fijo de h(x) (es decir, se cumple que 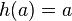 ), entonces se tienen 3 posibilidades: O Ψ(a)=0, o Ψ(a)=∞ o s=1. Por tanto, dado que Ψ(a) es finito yΨ (a) no se anula ni diverge, el autovalor s está dado por s = h' (a).
), entonces se tienen 3 posibilidades: O Ψ(a)=0, o Ψ(a)=∞ o s=1. Por tanto, dado que Ψ(a) es finito yΨ (a) no se anula ni diverge, el autovalor s está dado por s = h' (a).
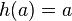 ), entonces se tienen 3 posibilidades: O Ψ(a)=0, o Ψ(a)=∞ o s=1. Por tanto, dado que Ψ(a) es finito yΨ (a) no se anula ni diverge, el autovalor s está dado por s = h' (a).
), entonces se tienen 3 posibilidades: O Ψ(a)=0, o Ψ(a)=∞ o s=1. Por tanto, dado que Ψ(a) es finito yΨ (a) no se anula ni diverge, el autovalor s está dado por s = h' (a).Significado en teoría de funciones
Para a = 0, si h es analítica en el disco unidad centrado en 0, y 0 < |h′(0)| < 1, Koenigs demostró en 1884 que existe una solución analítica (no trivial) Ψ que satisface la ecuación de Schröder. Este fue uno de los primeros pasos de una larga línea fructífera de teoremas en torno a la comprensión del operador de composición en espacios de funciones analíticas. Véase por ejemplo: función de Koenigs.
Las ecuaciones del tipo de la de Schröder son útiles para describir la autosimilaridad, y han sido extensivamente utilizadas en estudios de dinámica no lineal(coloquialmente teoría del caos). También ha sido utilizada en estudios de turbulencia, así como en el campo del grupo de renormalización.4 5
Una ecuación equivalente a la ecuación de Schröder es la fórmula que cumple su inversa respecto a la composición 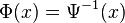 , que verifica
, que verifica
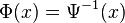 , que verifica
, que verifica
El cambio de variables α(x)=log(Ψ(x))/log(s) transforma a la ecuación de Schröder en la ecuación de Abel α(h(x)) = α(x)+1.
Igualmente, el cambio de variables Ψ(x) = log(φ(x)) transforma a la ecuación de Schröder en la ecuación de Böttcher φ(h(x))=(φ(x))s.
La n-ésima potencia de una solución de la ecuación de Schröder nos da otra solución de la ecuación de Schröder con autovalor sn. En la misma línea, dada una solución invertible Ψ(x) de la ecuación de Schröder, la función (no invertible) Ψ(x) k(logΨ(x)) es también solución de la misma ecuación para cualquier función periódica k(x)con periodo log(s). Todas las soluciones de la ecuación de Schröder están relacionadas de esta manera.
Soluciones
La ecuación de Schröder fue resuelta analíticamente para todo punto fijo a atractor (pero no superatractor), esto es, si se cumple que 0 < |h'(a)| < 1 por Gabriel Koenigs(1884).6 7
En el caso del punto fijo superatractor, |h'(a)| = 0, la ecuación de Schröder es complicada de estudiar, y se ha visto que es mejor transformarla a la ecuación de Böttcher.8
El mismo Schröder, en su artículo original de 1870,1 dio un buen número de soluciones particulares de la ecuación.
El desarrollo en serie en torno a un punto fijo, las propiedades de convergencia pertinentes de la solución para la órbita resultante y sus propiedades analiticidad fueron convincentemente explicadas por Szekeres.9 Una buena cantidad de las soluciones conocidas se han construido a partir de series asintóticas, véase matriz de Calerman.
Aplicaciones
Esta ecuación se ha usado para estudiar sistemas dinámicos discretos mediante la búsqueda de un nuevo sistema de coordenadas en el que el sistema (órbita) generado por h (x) sea más simple, una simple dilatación.
Más específicamente, en un sistema en el cual, en una unidad discreta de tiempo, x se transforma en h (x) (x → h(x)), se puede obtener su órbita (o flujo) suave a partir de la solución no de la ecuación de Schröder, si no de su ecuación conjugada.
Esta solución es:
En general, esta solución se puede iterar y así se puede obtener una solución (órbita en el lenguaje de sistemas dinámicos) válida para todo tiempo t como:
para t real, no necesariamente positivo o entero. Esto es, la solución forma un grupo continuo uniparamétrico completo bajo el parámetro t. Véase función iterada.
El conjunto  de todas las iteraciones enteras de
de todas las iteraciones enteras de 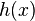 (semigrupo) se denomina splinter (o secuencia de Picard) de
(semigrupo) se denomina splinter (o secuencia de Picard) de 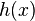 .
.
 de todas las iteraciones enteras de
de todas las iteraciones enteras de 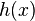 (semigrupo) se denomina splinter (o secuencia de Picard) de
(semigrupo) se denomina splinter (o secuencia de Picard) de 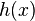 .
.
Sin embargo, todas las iteraciones (fraccionarias, infinitesimales, o negativas) de h(x) están dadas del mismo modo a través de la función Ψ(x) solución de la ecuación de Schröder. En10 se ha obtenido una interpolación continua de la recursividad discreta inicial x → h(x), de hecho, para toda la órbita.
De hecho, la raíz cuadrada funcional es h½(x) = Ψ−1 (s1/2 Ψ(x) ), por lo que h½( h½(x) ) = h (x), y así los demás casos.
Por ejemplo,11 algunos casos especiales de la ecuación logística como el caso caótico h(x)=4x(1−x) fueron estudiados ya por Schröder en su artículo original1 (cf. p. 306), Ψ(x)=arcsin2(√x), s=4, y por tantoht(x)=sin2(2t arcsin(√x)).
De hecho, se ve esta solución como resultado del movimiento dictado por una secuencia de potenciales de zigzag,12V(x) ∝ x(x−1) (nπ+arcsin √x)2, lo que es una característica genérica de las iteraciones continuas efectuadas por la ecuación de Schröder.
Como ejemplo de un caso no caótico también estudiado con su método tenemos, h(x)=2x(1−x), devuelveΨ(x)=−½ln(1−2x) y, por tanto ht(x)=−½((1−2x)2t−1).
secante hiperbólica de un número real  , es una función hiperbólicadefinida como la inversa del coseno hiperbólico. Se simboliza
, es una función hiperbólicadefinida como la inversa del coseno hiperbólico. Se simboliza  y matemáticamente se sintetiza:
y matemáticamente se sintetiza:
 , es una función hiperbólicadefinida como la inversa del coseno hiperbólico. Se simboliza
, es una función hiperbólicadefinida como la inversa del coseno hiperbólico. Se simboliza  y matemáticamente se sintetiza:
y matemáticamente se sintetiza: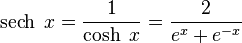
- El dominio de la función está definido de
 a
a  y su codominio queda en el intervalo
y su codominio queda en el intervalo ![(0,1]](https://upload.wikimedia.org/math/6/6/8/668c7b55a37300c330dcd565d9e076da.png) . La función presenta una asíntota horizontal en
. La función presenta una asíntota horizontal en 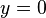 .Toma el nombre de hiperbólica por la oportunidad de poder utilizar u = acosht, v =bsenht, siendo t un número real, como ecuaciones paramétricas de una rama de la hipérbola de ecuación:1
.Toma el nombre de hiperbólica por la oportunidad de poder utilizar u = acosht, v =bsenht, siendo t un número real, como ecuaciones paramétricas de una rama de la hipérbola de ecuación:1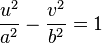
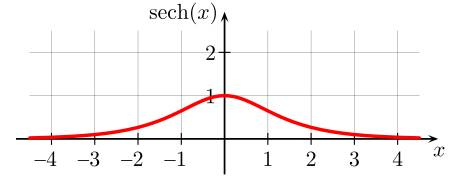 Gráfica de la función secante hiperbólica.
Gráfica de la función secante hiperbólica.- semi-continuidad es una propiedad de la funciones reales más débil que el concepto de continuidad. Coloquialmente, una función real se dice semi-continua superiormente en un punto x0 si los valores de la función en puntos cercanos a x0 son próximos a f(x0) o menores que f(x0). Similarmente si los valores de la función en dicho entorno son "mayores que" en vez de "menores que", decimos que la función es semi-continua inferiormente en x0.
Ejemplos
Consideremos la siguiente función definida por tramos, f(x) = –1 si x < 0 y f(x) = 1 si x ≥ 0. Ésta función es semi-continua superiormente pero no inferiormente.La función de parte entera, , que asigna a cada número real el entero menor o igual a dicho número es semi-continua superiormente en todo su dominio, similarmente
, que asigna a cada número real el entero menor o igual a dicho número es semi-continua superiormente en todo su dominio, similarmente 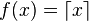 , que asigna a cada número real el entero mayor o igual a dicho número, es semi-continua inferiormente en todo su dominio.Una función puede ser semi-continua inferiormente o superiormente sin necesariamente ser continuas por la derecha o por la izquierda como podemos ver con el siguiente ejemplo:
, que asigna a cada número real el entero mayor o igual a dicho número, es semi-continua inferiormente en todo su dominio.Una función puede ser semi-continua inferiormente o superiormente sin necesariamente ser continuas por la derecha o por la izquierda como podemos ver con el siguiente ejemplo: una función que es semi-continua superiormente en x = 1 pero que no es continua por la derecha o por la izquierda. El límite por la derecha es 1 mientras que el límite por la izquierda es 1/2. Similarmente:
una función que es semi-continua superiormente en x = 1 pero que no es continua por la derecha o por la izquierda. El límite por la derecha es 1 mientras que el límite por la izquierda es 1/2. Similarmente: es semi-continua superormente en x = 0 pero sus límites por la derecha o por la izquierda no existen para dicho punto.
es semi-continua superormente en x = 0 pero sus límites por la derecha o por la izquierda no existen para dicho punto.- serie formal de potencias (a veces serie de potencias formal) a una expresión matemática que extiende las propiedades de las series de potencias en cuerpos como el de los reales o el de los complejos, permitiendo dar sentido formal a diversas notaciones que técnicamente carecen de rigurosidad. Las series formales de potencias tienen diversas aplicaciones, pudiéndose mencionar la combinatoria y la teoría de números.
Definición
Informalmente podemos pensar que una serie de potencias formal es una serie infinita de términos de la forma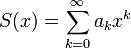 esto es, un polinomio con infinitos términos, en que los ak son elementos de un cuerpo. Para formalizar esto, consideremos el conjunto de todas las sucesiones infinitas de elementos de un cuerpo
esto es, un polinomio con infinitos términos, en que los ak son elementos de un cuerpo. Para formalizar esto, consideremos el conjunto de todas las sucesiones infinitas de elementos de un cuerpo , las cuales representaremos de esta forma:
, las cuales representaremos de esta forma: Denotaremos al conjunto de todas estas sucesiones con el símbolo
Denotaremos al conjunto de todas estas sucesiones con el símbolo . Definimos la suma de estas sucesiones de la siguiente forma:
. Definimos la suma de estas sucesiones de la siguiente forma: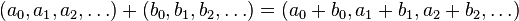 y su ponderación (multiplicación por escalar) por un elemento del cuerpo
y su ponderación (multiplicación por escalar) por un elemento del cuerpo como:
como: Esto le da al conjunto
Esto le da al conjunto una estructura de espacio vectorial sobre
una estructura de espacio vectorial sobre  , como puede comprobarse directamente. Ahora definimos el producto entre dos sucesiones de
, como puede comprobarse directamente. Ahora definimos el producto entre dos sucesiones de  según la fórmula:
según la fórmula: en que, si
en que, si , el término general ck es:
, el término general ck es: Nótese que esta definición coincide con la de producto de Cauchy de dos sucesiones. Asimismo, si multiplicamos dos polinomios (o dos series absolutamente convergentes) con coeficientes reales o complejos, vemos que los coeficientes del resultado siguen una regla análoga. Por lo mismo esta definición es coherente desde un punto de vista intuitivo.Se puede demostrar por la definición que la operación
Nótese que esta definición coincide con la de producto de Cauchy de dos sucesiones. Asimismo, si multiplicamos dos polinomios (o dos series absolutamente convergentes) con coeficientes reales o complejos, vemos que los coeficientes del resultado siguen una regla análoga. Por lo mismo esta definición es coherente desde un punto de vista intuitivo.Se puede demostrar por la definición que la operación en
en  es conmutativa, asociativa y distributiva, lo que implica que
es conmutativa, asociativa y distributiva, lo que implica que 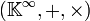 es una
es una  -álgebra lineal conmutativa con unidad, es decir, una estructura algebraica que es tanto espacio vectorial como anillo conmutativo con unidad, siendo el elemento neutro la sucesión 1 = (1,0,0,...).Adoptaremos, como es habitual, la notación
-álgebra lineal conmutativa con unidad, es decir, una estructura algebraica que es tanto espacio vectorial como anillo conmutativo con unidad, siendo el elemento neutro la sucesión 1 = (1,0,0,...).Adoptaremos, como es habitual, la notación . Denotaremos por x a la sucesión (0,1,0,0,...). Nótese que en el resto de este artículo la letra x denotará a dicha sucesión y no a una variable. Tenemos entonces:
. Denotaremos por x a la sucesión (0,1,0,0,...). Nótese que en el resto de este artículo la letra x denotará a dicha sucesión y no a una variable. Tenemos entonces: etc. Tenemos entonces la igualdad:
etc. Tenemos entonces la igualdad: Esta es la definición de una serie formal de potencias. Nótese que el conjunto de las series de potencias para los cuales existe un índice k que satisface que an = 0 para todo n > k es una sub-álgebra lineal de
Esta es la definición de una serie formal de potencias. Nótese que el conjunto de las series de potencias para los cuales existe un índice k que satisface que an = 0 para todo n > k es una sub-álgebra lineal de isomorfa al conjunto de las funciones polinomios en el cuerpo
isomorfa al conjunto de las funciones polinomios en el cuerpo  (a menos que dicho cuerpo sea finito). En general, denotamos a ambos conjuntos con el símbolo
(a menos que dicho cuerpo sea finito). En general, denotamos a ambos conjuntos con el símbolo ![\mathbb{K}[x]](https://upload.wikimedia.org/math/d/d/f/ddf3e61714833d45bad11d235837b772.png) y no hacemos distinción entre una serie formal finita y un polinomio.Nótese que en el concepto de serie formal de potencias la notación
y no hacemos distinción entre una serie formal finita y un polinomio.Nótese que en el concepto de serie formal de potencias la notación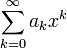 es solamente una expresión conveniente y no alude en ninguna forma a la convergencia o divergencia de la serie, o a asignarle un valor. Se reitera que x representa a la sucesión (0,1,0,0...) y no es una variable. En el caso de una serie finita (polinomio) existe una forma de asignarle directamente un valor, lo que se analizará posteriormente.1
es solamente una expresión conveniente y no alude en ninguna forma a la convergencia o divergencia de la serie, o a asignarle un valor. Se reitera que x representa a la sucesión (0,1,0,0...) y no es una variable. En el caso de una serie finita (polinomio) existe una forma de asignarle directamente un valor, lo que se analizará posteriormente.1Asignación de un valor a una serie de potencias formal
A pesar de que el trabajo con una serie de potencias formal no involucra de ninguna forma el asignarle un valor a una serie , podemos, si es conveniente, asignar en ciertos casos un número a una serie de potencias S, de la siguiente forma:Sea
, podemos, si es conveniente, asignar en ciertos casos un número a una serie de potencias S, de la siguiente forma:Sea una
una  -álgebra lineal con unidad, i.e. un espacio vectorial
-álgebra lineal con unidad, i.e. un espacio vectorial 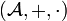 sobre
sobre  con una segunda operación
con una segunda operación 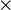 que le da a
que le da a 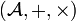 una estructura de anillo con unidad. Como antes, dado un elemento
una estructura de anillo con unidad. Como antes, dado un elemento 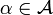 , denotamos
, denotamos 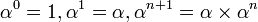 , en que 1 es el elemento unidad de
, en que 1 es el elemento unidad de  (como es usual). Entonces, dada una serie finita o polinomio formal
(como es usual). Entonces, dada una serie finita o polinomio formal ![S(x) = (s_0x^0 + s_1x^1 + s_2x^2 + \dots + s_nx^n) \in \mathbb{K}[x]](https://upload.wikimedia.org/math/6/3/0/63065a933283636ca76a5ead6fd01c2c.png) , se le asigna a cada
, se le asigna a cada 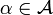 un elemento de
un elemento de  dado por:
dado por: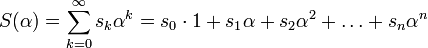 Por ejemplo, si
Por ejemplo, si![P(x) = (1 + x^2 - 3x^4) \in \mathbb{R}[x]](https://upload.wikimedia.org/math/b/1/1/b119bd72600743df785d168e23e619fd.png) , se tiene que
, se tiene que 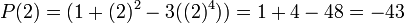 .Para asignar de una forma análoga un valor a una serie de potencias formal infinita se deben introducir los conceptos de límite y convergencia, para lo cual es necesario definir una topología sobre el conjunto
.Para asignar de una forma análoga un valor a una serie de potencias formal infinita se deben introducir los conceptos de límite y convergencia, para lo cual es necesario definir una topología sobre el conjunto . Por ejemplo, si consideramos la serie
. Por ejemplo, si consideramos la serie 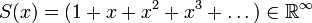 , podemos decir, por ejemplo, que:
, podemos decir, por ejemplo, que: y, en general:
y, en general: Sin embargo, por la forma en que se ha construido la topología de
Sin embargo, por la forma en que se ha construido la topología de , esto es, por la definición de límite en el cuerpo de los reales, la última igualdad es válida solamente cuando |x| < 1. Sin embargo, mediante manipulaciones algebraicas o analíticas puede asignársele un valor a otras series a pesar de que no converjan en sentido estricto (véase Serie divergente para más detalles), por ejemplo, dada la misma serie del ejemplo anterior, intentemos asignar mediante métodos del álgebra un valor a S(2):S(2) = 1 + 2 + 4 + 8 + ... = u2u = 2·1 + 2·2 + 2·4 + 2·8 + ... = 2 + 4 + 8 + 16 + ... = (1 + 2 + 4 + 8 + 16 + ...) - 1 = u - 12u = u - 1u = -1Podemos ver que, a pesar de que esto en sentido estricto no es correcto, es un resultado coherente y podemos considerarlo válido en cierto contexto en que se requiera que S(2) tenga un valor.
, esto es, por la definición de límite en el cuerpo de los reales, la última igualdad es válida solamente cuando |x| < 1. Sin embargo, mediante manipulaciones algebraicas o analíticas puede asignársele un valor a otras series a pesar de que no converjan en sentido estricto (véase Serie divergente para más detalles), por ejemplo, dada la misma serie del ejemplo anterior, intentemos asignar mediante métodos del álgebra un valor a S(2):S(2) = 1 + 2 + 4 + 8 + ... = u2u = 2·1 + 2·2 + 2·4 + 2·8 + ... = 2 + 4 + 8 + 16 + ... = (1 + 2 + 4 + 8 + 16 + ...) - 1 = u - 12u = u - 1u = -1Podemos ver que, a pesar de que esto en sentido estricto no es correcto, es un resultado coherente y podemos considerarlo válido en cierto contexto en que se requiera que S(2) tenga un valor.
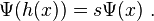


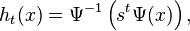



No hay comentarios:
Publicar un comentario