cosecante hiperbólica de un número real  , es una función hiperbólica definida como lainversa del seno hiperbólico. Se simboliza
, es una función hiperbólica definida como lainversa del seno hiperbólico. Se simboliza  o
o  , y matemáticamente se sintetiza:
, y matemáticamente se sintetiza:
 , es una función hiperbólica definida como lainversa del seno hiperbólico. Se simboliza
, es una función hiperbólica definida como lainversa del seno hiperbólico. Se simboliza  o
o  , y matemáticamente se sintetiza:
, y matemáticamente se sintetiza:Características
El dominio y su codominio está definido en  y
y 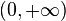 , es decir, sólo queda definida para todos los valores salvo x=0 e y=0.
, es decir, sólo queda definida para todos los valores salvo x=0 e y=0.
 y
y 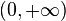 , es decir, sólo queda definida para todos los valores salvo x=0 e y=0.
, es decir, sólo queda definida para todos los valores salvo x=0 e y=0.
Gráfica de la función cosecante hiperbólica.
cotangente hiperbólica de un número real  , es una función hiperbólica definida como lainversa de la tangente hiperbólica. Se simboliza
, es una función hiperbólica definida como lainversa de la tangente hiperbólica. Se simboliza 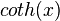 o
o 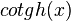 y matemáticamente se sintetiza:
y matemáticamente se sintetiza:
 , es una función hiperbólica definida como lainversa de la tangente hiperbólica. Se simboliza
, es una función hiperbólica definida como lainversa de la tangente hiperbólica. Se simboliza 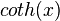 o
o 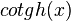 y matemáticamente se sintetiza:
y matemáticamente se sintetiza:
- El dominio de la función está definido para
 y
y 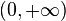 y su codominio queda definido para el intervalo
y su codominio queda definido para el intervalo  y
y  . La función presenta unaasíntota horizontal en
. La función presenta unaasíntota horizontal en  y en
y en  . A ambos lados de la asíntota nos encontramos una función monótona estrictamente decreciente.
. A ambos lados de la asíntota nos encontramos una función monótona estrictamente decreciente.Derivación
La derivada de la función es:Teorema de adición
La función cotangente hiperbólica, como demuestra el teorema de adición, se puede sintetizar en:
 Gráfica de la función cotangente hiperbólica.
Gráfica de la función cotangente hiperbólica.- crecimiento hiperbólico.1 Con más precisión, la función recíproca
 tiene una hipérbola como gráfico con singularidad en 0, lo que significa que el límite de
tiene una hipérbola como gráfico con singularidad en 0, lo que significa que el límite de 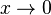 es infinito o asintótico: cualquier gráfico similar muestra tal crecimiento.
es infinito o asintótico: cualquier gráfico similar muestra tal crecimiento. - Si el resultado de una función es inversamente proporcional a su insumo, o inversamente proporcional a la diferencia de un valor dado
 , la función mostrará un crecimiento hiperbólico, con una singularidad en
, la función mostrará un crecimiento hiperbólico, con una singularidad en  .En el mundo real es un crecimiento creado por ciertos mecanismos no lineales.2
.En el mundo real es un crecimiento creado por ciertos mecanismos no lineales.2Comparaciones con otros tipos de crecimiento=
Del mismo modo que los crecimientos exponencial y el logístico, el hiperbólico es no lineal, pero se distinguen en varios aspectos. Las tres funciones presentan convexidad, sin embargo su comportamiento asintótico es muy diferente:- El crecimiento logístico está restringido (límite finito aun cuando el tiempo sea infinito),
- El crecimiento exponencial crece hasta infinito si el tiempo es infinito (pero siempre es finito si el tiempo es finito),
- El crecimiento hiperbólico tiene una singularidad en tiempo finito (crece hasta infinito con tiempo finito).
Aplicaciones
Población
Ciertos modelos matemáticos sugieren que hasta la década de 1970 la población mundial experimentó un crecimiento hiperbólico (véase, por ejemplo,[1] Introduction to Social Macrodynamics por Andrey Korotayev et al.). También se demostró que hasta la década de 1970 el crecimiento hiperbólico de la población mundial fue acompañada por un crecimiento cuadrático-hiperbólico del PIB mundial, y se han desarrollado una serie de modelos matemáticos que describen tanto este fenómeno. El crecimiento hiperbólico de la población mundial y el crecimiento cuadrática-hiperbólico del PIB mundial observados hasta la década de 1970 se han correlacionado por Andrey Korotayev y sus colegas para una segunda opinión positiva orden no lineal entre el crecimiento demográfico y el desarrollo tecnológico, descrito por una cadena de la causalidad: el crecimiento tecnológico conduce a una mayor capacidad de carga de la tierra para la gente, lo que lleva a más personas, lo que conduce a más inventores, que a su vez conduce a un crecimiento aún más tecnológico. 3 Otros modelos sugieren un crecimiento exponencial, logístico crecimiento, u otras funciones.Ejemplo matemático
La funciónpresenta crecimiento hiperbólico con una singularidad en el momento : en el límite de
: en el límite de  , la función llega a infinito.In extenso, la funciónpresenta crecimiento hiperbólico, donde
, la función llega a infinito.In extenso, la funciónpresenta crecimiento hiperbólico, donde es un factor de escala.Hay que percibir que esta función algebraica puede contemplarse como solución analítica para la función diferencial:4Esto significa que con el crecimiento hiperbólico la tasa de crecimiento absoluto de la variable x en el momento t es proporcional al cuadrado del valor de x en el momento t.Respectivamente, la función cuadrático-hiperbólica es tal como sigue:
es un factor de escala.Hay que percibir que esta función algebraica puede contemplarse como solución analítica para la función diferencial:4Esto significa que con el crecimiento hiperbólico la tasa de crecimiento absoluto de la variable x en el momento t es proporcional al cuadrado del valor de x en el momento t.Respectivamente, la función cuadrático-hiperbólica es tal como sigue:
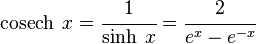
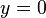 y otra
y otra  .
.
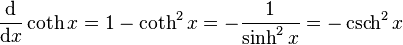
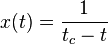

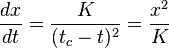

No hay comentarios:
Publicar un comentario