Criterio de d'Alembert se utiliza para determinar la convergencia o divergencia de una serie de términos positivos cualquiera, y por tanto, hacer una clasificación de la misma.
Definiendo con  a la variable independiente de la sucesión, dicho criterio establece que si llamamos
a la variable independiente de la sucesión, dicho criterio establece que si llamamos  al límite para
al límite para  tendiendo a infinito de
tendiendo a infinito de 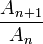 se obtiene un número
se obtiene un número  , con los siguientes casos:
, con los siguientes casos:
 a la variable independiente de la sucesión, dicho criterio establece que si llamamos
a la variable independiente de la sucesión, dicho criterio establece que si llamamos  al límite para
al límite para  tendiendo a infinito de
tendiendo a infinito de 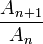 se obtiene un número
se obtiene un número  , con los siguientes casos:
, con los siguientes casos:- Si
 converge.
converge. - Si
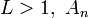 diverge.
diverge. - Si
 , el criterio no decide y es necesario calcular el límite de otro modo.
, el criterio no decide y es necesario calcular el límite de otro modo.
El criterio de D'Alembert se utiliza para clasificar las series numéricas. Podemos enunciarlo de la siguiente manera:
Sea: 

Tal que:
 (o sea una sucesión de términos positivos) y
(o sea una sucesión de términos positivos) y tienda a cero cuando
tienda a cero cuando  tiende a infinito (condición necesaria de convergencia)
tiende a infinito (condición necesaria de convergencia)
Se procede de la siguiente manera:
 con
con  tendiendo a infinito.
tendiendo a infinito.
Así obtenemos  y se clasifica de la siguiente manera:
y se clasifica de la siguiente manera:
 y se clasifica de la siguiente manera:
y se clasifica de la siguiente manera: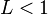 la serie converge
la serie converge la serie diverge
la serie diverge el criterio no sirve hay que aplicar otro criterio.
el criterio no sirve hay que aplicar otro criterio.
Ejemplo
Sea: 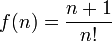
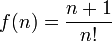
Clasificar 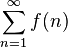
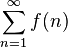
a)

b) 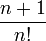 tiende a cero conforme crece
tiende a cero conforme crece  (porque el factorial crece más rápidamente que n+1)
(porque el factorial crece más rápidamente que n+1)
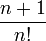 tiende a cero conforme crece
tiende a cero conforme crece  (porque el factorial crece más rápidamente que n+1)
(porque el factorial crece más rápidamente que n+1)
c) Aplicando D'Alembert:
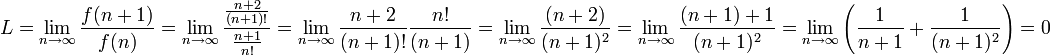
y como 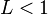 , la serie
, la serie 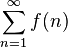 converge.
converge.
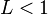 , la serie
, la serie 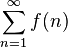 converge.
converge.- Criterio del cociente (de D'Alembert):
* Si 
entonces la serie  es convergente.
es convergente.
Sin embargo,
* si  ( incluso si l fuera infinito positivo)
( incluso si l fuera infinito positivo)
entonces la serie  es divergente.
es divergente.
La desigualdad de Hardy es una desigualdad matemática llamada así debido a G.H. Hardy. Esta desigualdad afirma que si  es una sucesión de números reales no negativos que no es idénticamente nula, entonces para cualquier número real p > 1 se tiene
es una sucesión de números reales no negativos que no es idénticamente nula, entonces para cualquier número real p > 1 se tiene
 es una sucesión de números reales no negativos que no es idénticamente nula, entonces para cualquier número real p > 1 se tiene
es una sucesión de números reales no negativos que no es idénticamente nula, entonces para cualquier número real p > 1 se tiene
Una versión integral de la desigualdad de Hardy afirma que que si f es una función integrable a valores no-negativos, entonces
con igualdad si y solo si f(x) = 0 casi en todas partes.
Historia
La desigualdad de Hardy fue publicada y demostrada por primera vez (al menos en su versión discreta e involucrando una constante no-optimal) en 1920 en una nota de Hardy.
desigualdad de Hölder, llamada así debido a Otto Hölder, es una desigualdad fundamental entre integrales y una herramienta indispensable para el estudio de los espacios Lp.
Sea (S, Σ, μ) un espacio de medida y sea 1 ≤ p, q ≤ ∞ con 1/p + 1/q = 1. Entonces, para toda función medible de valores reales o complejos f y g sobre S, se tiene que
Los números p y q expresados arriba se dice que son conjugados de Hölder uno del otro. El caso especial p = q = 2 se reduce a la conocida desigualdad de Cauchy-Schwarz.
La desigualdad de Hölder se cumple incluso si ||fg ||1 es infinita, siendo para el miembro derecho de la desigualdad infinito en ese caso. En particular, si f está en Lp(μ) yg está en Lq(μ), entonces fg está en L1(μ).
Para 1 < p, q < ∞, f ∈ Lp(μ) y g ∈ Lq(μ), la desigualdad de Hölder se convertirá en una igualdad si y sólo si |f |p y |g |q son linealmente dependientes en L1(μ), lo que significa que existen dos números reales α, β ≥ 0, siendo alguno de ellos distinto de 0, tales que α |f |p = β |g |q μ-casi en todas partes.
La desigualdad de Hölder es usada para demostrar la desigualdad de Minkowski, la cual es una generalización de la desigualdad triangular en el espacio Lp(μ), y también para establecer que Lq(μ) es el espacio dual de Lp(μ) para 1 ≤ p < ∞.
La desigualdad de Hölder fue descubierta por primera vez por Rogers (1888), y descubierta independientemente por Hölder (1889).
desigualdad del triángulo es un teorema de geometría euclidiana que establece:
Este resultado ha sido generalizado a otros contextos más sofisticados como espacios vectoriales. Definido matemáticamente, cualquier triángulo cumple la siguiente propiedad:
donde a, b y c son los lados.
Espacios vectoriales normados
El teorema puede generalizarse a espacios vectoriales normados, obteniéndose la siguiente versión de la desigualdad triangular:
|
Es decir, que La norma de la suma de dos vectores es siempre menor o igual a la suma de las normas de los dos vectores.
En el caso particular de considerar la recta real como espacio vectorial normado con el valor absoluto como norma obtenemos la siguiente versión del teorema:
|
cuya demostración es:
Demostración
(Ámbito → ℝ). Haciendo uso de las propiedades del valor absoluto, es posible escribir:
Sumando ambas inecuaciones:
A su vez, usando la propiedad de valor absoluto 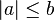 si y solo si
si y solo si  en la línea de arriba queda:
en la línea de arriba queda:
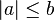 si y solo si
si y solo si  en la línea de arriba queda:
en la línea de arriba queda:Generalización de la desigualdad triangular
La desigualdad triangular puede generalizarse a un número arbitrario de sumandos:
,
es decir:
donde n es un número natural, y los 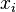 son números reales.
son números reales.
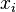 son números reales.
son números reales.| Demostración |
Esta desigualdad puede generalizarse aún más para integrales (Riemann, Riemann-Stieltjes, Lebesgue-Stieltjes, etc):


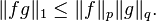

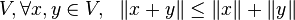

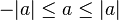
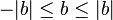



No hay comentarios:
Publicar un comentario