Las constantes Du Bois Reymond, (Paul David Gustav) 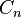 están definidas por
están definidas por
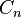 están definidas por
están definidas por
Estas constantes pueden también escribirse como:
donde 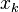 es la k-ésima raíz de
es la k-ésima raíz de
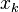 es la k-ésima raíz de
es la k-ésima raíz de
Además tenemos la siguiente serie
En el siguiente gráfico se ve la representación de la función
para los primeros cuatro valores de 

La integración numérica de esta función es difícil. Los cuatro primeros valores de estas constantes son:
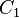 diverge
diverge


-

- Las constantes
definidas por
(1)Estas constantes también pueden escribirse como las sumas(2)y(3)(E. Weisstein 3 de febrero, 2015), dondees la
raíz positiva ª de
(4)yes la función sinc.
diverge, con el primer pocos constante posterior numéricamente dada por
(5)(6)(7)Sorprendentemente, las constantes du Bois Reymond incluso ordenadas (y, enparticular,; Le Lionnais 1983) se pueden calcular analíticamente como polinomios
en,
(8)(9)(10)(OEIS A085466 y A085467) como se encuentra por Watson (1933). Para enteropositivo, éstos tienen la fórmula explícita
(11) - En análisis matemático una función f(x) se dice que es uniformemente continua si pequeños cambios en el valor de x producen pequeños cambios en el valor de la función (continuidad) y el tamaño de los cambios en f(x) depende solo del tamaño de los cambios en x pero no del valor de x (uniforme).
- Dados dos espacios métricos
 y
y  , y
, y 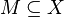 entonces una función
entonces una función  se llama uniformemente continua en M si para cualquier número real
se llama uniformemente continua en M si para cualquier número real  existe
existe 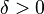 tal que
tal que  , se tiene que
, se tiene que 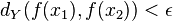 para todo
para todo  .
.
Una función es uniformemente continua en un intervalo
es uniformemente continua en un intervalo  si para todo
si para todo  existe algún
existe algún 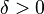 tal que para todo
tal que para todo  se cumple que si
se cumple que si  , entonces
, entonces  .1
.1
A diferencia de en la continuidad, donde el valor de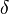 depende del punto x, en las funciones uniformemente continuas, no.
depende del punto x, en las funciones uniformemente continuas, no.Ejemplos
- La función 1/x con x>0 es continua pero no uniformemente continua
- La función x es uniformemente continua en el intervalo [0,1].
- Todo polinomio
 cuyo grado sea mayor o igual que uno es uniformemente continuo en un intervalo cerrado.
cuyo grado sea mayor o igual que uno es uniformemente continuo en un intervalo cerrado.
Resultados
- De la definición se deduce que toda función uniformemente continua es continua. Lo contrario (toda función continua es uniformemente continua) no siempre es cierto. Ejemplo: Si
 y
y 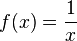 .
.  es continua y no es uniformemente continua. Sin embargo, se verifica que:
es continua y no es uniformemente continua. Sin embargo, se verifica que:
Si M es un espacio métrico compacto e Y un espacio métrico, entonces toda función continua f : M → Y es uniformemente continua. En particular, toda función continua sobre un intervalo cerrado y acotado es uniformemente continua en dicho intervalo (Teorema de Heine-Cantor).- Si (xn) es una sucesión de Cauchy contenida en el dominio de f (no necesariamente convergente) y f es una función uniformemente continua, entonces (f(xn)) también es una sucesión de Cauchy.
- Toda función Lipschitz continua es uniformemente continua.
- Sea
I un intervalo de la recta real yf:I→R una función. Se dice quef es uniformemente continua enI si y sólo si, para todoϵ>0 , existeδ>0 tal que:|x−y|<δ,x∈I,y∈I⇒|f(x)−f(y)|<ϵ.
TEOREMA. Toda función uniformemente continua es continua.
Sin embargo, no toda función continua es uniformemente continua.TEOREMA (de caracterización de la continuidad uniforme por sucesiones). SeaI⊂R intervalo yf:I→R una función. Entonces,f es uniformemente continua si y sólo si para cualquier par de sucesiones(xn) e(yn) de puntos deI tales que(xn−yn)→0 se verifica(f(xn)−f(yn))→0 .TEOREMA (de Heine). Seana,b∈R cona<b yf:[a,b]→R una función continua. Entonces,f es uniformemente continua. - Demostrar que
f:R→R dada porf(x)=2x+5 es uniformemente continua.

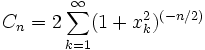
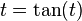
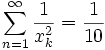

 .
.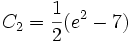
No hay comentarios:
Publicar un comentario