AMIGOS PARA SIEMPRE: Análisis matemático

Campo vectorial : :

Definición de campo vectorial

Físicamente un campo vectorial representa la distribución espacial de una magnitud vectorial.

Matemáticamente se define un campo vectorial como una función vectorial de las coordenadas o como un caso especial de una transformación no necesariamente lineal.

, en donde

representa el espacio vectorial que hace las veces de dominio y

el espacio vectorial que actúa como rango.

El campo ilustrado en la ecuación anterior es un campo vectorial

, dado que la función vectorial tiene tres componentes y cada componente es una función de tres variables independientes.

Cuando se modela la distribución de esfuerzos en una estructura, la distribución de fuerzas de naturaleza electromagnética o gravitatoria en el espacio, se hace usando campos vectoriales.

Otros ejemplos de campos vectoriales son las funciones de velocidad asociadas a las trayectorias de las partículas o diferenciales de volumen de una sustancia en condiciones de flujo bien sea laminar o turbulento.

El gradiente de un campo escalar, constituye un ejemplo adicional de campo vectorial, dado que la magnitud y dirección del gradiente de un campo escalar es una función de las coordenadas, tal como se ilustró en la Figura 19.

Representación de un campo vectorial

Líneas de fuerza

La representación de los campos vectoriales se hace mediante mapas semejantes a los de los campos escalares, pero usando líneas que representan la continuidad de la orientación de los vectores de campo sobre una región definida. Estas líneas reciben el nombre de líneas de fuerza.

Al igual que con los campos escalares, un campo vectorial no puede representarse fácilmente en tres dimensiones, por lo que normalmente se hacen proyecciones sobre los planos directores del sistema de coordenadas.

Figura 20 Representación de un campo vectorial de

Las líneas de fuerza cumplen con las siguientes propiedades:

Los vectores de campo en cualquier punto son siempre tangenciales a la línea de fuerza que pasa por el punto dado.
Las líneas de fuerza no se cruzan en ningún punto aunque pueden seguir trayectorias cerradas.
La cantidad de líneas de fuerza en cualquier porción del espacio en que se encuentra definido el campo es proporcional a la intensidad del campo vectorial.

En algunas otras ocasiones, la representación de campos vectoriales se hace a través de los vectores de campo directamente. En estos casos, la intensidad del campo vectorial se asocia a la densidad de vectores de campo en una región, tanto como a la longitud de los mismos.

Trazado de las líneas de fuerza de un campo vectorial

De acuerdo con la definición de línea de fuerza, una línea de fuerza es tangente a los vectores de campo en todos los puntos del espacio vectorial definido. Esto, se ilustra gráficamente en la Figura 21 .

Figura 21 Relación entre los vectores de campo y la recta tangente a la curva en una línea de fuerza.

Se observa claramente que el vector de campo tiene la misma dirección de la recta tangente a la línea de fuerza en el punto de tangencia.

En este caso, el vector de campo tiene dos componentes denominados

respectivamente; resulta entonces que la relación entre las componentes del vector da como resultado la pendiente de la recta tangente a la línea de fuerza en cada punto de tangencia.

Dado que la pendiente de la recta tangente es la derivada de la curva, se puede entonces proponer una igualdad definida por:

La familia de soluciones a esta ecuación diferencial es entonces la misma familia de curvas que representa las líneas de fuerza.

Para el caso considerado en el Ejemplo 18 , el campo vectorial tiene por ecuación:

En este caso, la ecuación diferencial planteada quedaría:

La familia de soluciones de esta ecuación es de la forma:

Para diferentes valores de k tanto negativos como positivos se obtienen diferentes líneas de fuerza según se ilustra en la Figura 22 .

Figura 22 Trazado de las líneas de fuerza del campo vectorial del Ejemplo 18 .

Finalmente, la dirección de las líneas de fuerza la define la ecuación del campo vectorial, por ejemplo en el primer cuadrante, tanto x como y tienen signo positivo, por lo cual las líneas de fuerza van en la dirección del semieje x positivo y del semieje y negativo.

El mismo método de análisis se usa para definir la dirección en los cuatro cuadrantes.

Como se observa al comparar las gráficas de las líneas de fuerza y las obtenidas en el Ejemplo 17 , las líneas de fuerza son perpendiculares a las equipotenciales, como es de esperarse de acuerdo con las propiedades del vector gradiente.

Propiedades de un campo vectorial

Circulación y Rotacional

Cuando las líneas de fuerza en cualquier región del espacio donde se encuentre definido el campo siguen una trayectoria cerrada se dice que el campo posee circulación en dicha región.

La circulación es una característica de los campos vectoriales y tiene una definición matemática relativamente simple.

La circulación de un campo es la sumatoria sobre una trayectoria cerrada de las componentes de campo tangenciales la trayectoria.

Figura 23 Líneas de fuerza de un campo vectorial con circulación.

Cuando se desea medir la circulación de un campo vectorial como una función de las coordenadas, se utiliza una función vectorial denominada rotacional, que mide la circulación por unidad de área cuando el área tiende a cero en cada punto del espacio en que se encuentra definido el campo.

Donde C es la curva que encierra la superficie

El rotacional de un campo es una función de las coordenadas y puede en consecuencia, ser diferente para los diferentes puntos del espacio en que se encuentra definido el campo.

Cuando el rotacional es nulo en todos los puntos de una región, se dice que el campo es irrotacional o conservativo en dicha región.

En coordenadas generalizadas el operador vectorial diferencial del rotacional es el que se muestra en la Ecuación 24.

Ecuación 24 Rotacional en coordenadas generalizadas.

El rotacional en los demás sistemas de coordenadas se puede obtener a partir del desarrollo de la Ecuación 24 y se encuentra en la sección de anexos.

Teorema de Stokes

A partir de la definición de rotacional, se deduce una identidad conocida como el teorema de Stokes:

Dado que el rotacional de un campo vectorial es una especia de derivada areolar de la circulación del campo, es lógico pensar que la integral de área del rotacional corresponda a la circulación de campo, de donde se desprende la Ecuación 25.

Ecuación 25 Teorema de Stokes

La circulación de un campo vectorial a lo largo de cualquier trayectoria es igual al flujo del campo sobre cualquier superficie encerrada por dicha trayectoria.

Flujo y divergencia

El flujo de un campo vectorial A se define como la cantidad de líneas de fuerza que atraviesa la superficie y es una cantidad escalar. Para cuantificarlo, se toma solamente la componente normal de las líneas que inciden sobre la superficie.

La componente normal se obtiene como la proyección del vector de campo sobre un vector unitario perpendicular a la superficie, el cual fue definido en el capítulo anterior.

Figura 24 Flujo de un campo vectorial A a través de una superficie

Para las superficies cerradas se define también el flujo de salida como el flujo que atraviesa la superficie cuando el vector de superficie apunta siempre hacia fuera de la superficie cerrada

Figura 25 Flujo de salida de una superficie cerrada en presencia de una fuente, un sumidero o ninguno de ellos.

Cuando el flujo de salida es positivo, significa que en el interior de la superficie se encuentra una fuente de campo, es decir, que el número de líneas de fuerza que abandona la superficie es superior al número de líneas de fuerza que ingresan a ella.

Cuando el flujo de salida tiene signo negativo significa que en interior de la superficie se encuentra un sumidero, es decir el caso contrario a una fuente.

En general, las líneas de fuerza nacen en las fuentes y terminan en los sumideros.

El flujo de salida por unidad de volumen encerrado puede tomarse como una medida de la presencia de fuentes o sumideros en la región delimitada por la superficie.

Se denomina Divergencia de un campo vectorial al flujo de salida por unidad de volumen cuando la unidad de volumen se hace infinitesimal.

La divergencia de un campo vectorial es un campo escalar dada la naturaleza escalar del flujo y la naturaleza puntual de la divergencia.

El operador divergencia en coordenadas generalizadas es:

Ecuación 26 Divergencia en coordenadas generalizadas

La divergencia en los demás sistemas de coordenadas se encuentra en la sección de anexos.

un campo vectorial representa la distribución espacial de una magnitud vectorial. Es una expresión decálculo vectorial que asocia un vector a cada punto en el espacio euclidiano, de la forma

\varphi:\R^n \to \R^n

Los campos vectoriales se utilizan en física, por ejemplo, para representar la velocidad y la dirección de un fluido en el espacio, o la intensidad y la dirección de fuerzas como la gravitatoria o la fuerza electromagnética.

Como expresión matemática rigurosa, los campos vectoriales se definen en variedades diferenciables como secciones delfibrado tangente de la variedad. Este es el tipo de tratamiento necesario para modelizar el espacio-tiempo curvo de la teoría general de la relatividad por ejemplo.

Un campo vectorial sobre un subconjunto del espacio euclidiano

X \subset \R^n

es una función con valores vectoriales:

$\mathbf{F}: X \rightarrow \mathbb{R}^n \,$

Se dice que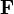

\mathbf{F}

es un campo vectorial C^k si como función es k veces diferenciable con continuidad en X. Un campo vectorial se puede visualizar como un espacio X con un vector n- dimensional unido a cada punto en X.

Operaciones con campos vectoriales

Dados dos campos vectoriales C^k F, G definidos sobre X y una función C^k a valores reales f definida sobre X, se definen las operaciones producto por escalar y adición:

$(f \mathbf{F})(\mathbf{x}) = f(\mathbf{x}) \mathbf{F}(\mathbf{x})$

Debido a la linealidad de la función (F+G):

$\mathbf{(F+G)}(\mathbf{x}) = \mathbf{F}(\mathbf{x}) + \mathbf{G}(\mathbf{x})$

define el módulo de los campos vectoriales C^k sobre el anillo de las funciones C^k. Alternativamente el conjunto de todos los campos vectoriales sobre un determinado subconjunto X es en sí mismo un espacio vectorial.

Derivación y potenciales escalares y vectores

Los campos vectoriales se deben comparar a los campos escalares, que asocian un número o escalar a cada punto en el espacio (o a cada punto de alguna variedad).

Las derivadas de un campo vectorial, que dan por resultado un campo escalar u otro campo vectorial, se llaman divergencia y rotor respectivamente. Recíprocamente:

Dado un campo vectorial cuyo rotacional se anula en un punto , existe un campo potencial escalar cuyo gradiente coincide con el campo escalar en un entorno de ese punto.
Dado un campo vectorial solenoidal cuya divergencia se anula en un punto, existe un campo vectorial llamado potencial vector cuyo rotacional coincide con el campo escalar en un entorno de ese punto.

Estas propiedades derivan del teorema de Poincaré.

Puntos estacionarios

Un punto

\scriptstyle x\in X

es estacionario si:

$\mathbf{F}(\mathbf{x}) = \mathbf{0}$

El conjunto de todos los espacios vectoriales definidos sobre un subconjunto X, que son estacionarios en un determinado punto forman un subespacio vectorial del conjunto del espacio vectorial definido en la sección anterior.

Ejemplos

Un campo vectorial para el movimiento del aire en la tierra asociará a cada punto en la superficie de la tierra un vector con la velocidad y la dirección del viento en ese punto. Esto se puede dibujar usando flechas para representar el viento; la longitud (magnitud) de la flecha será una indicación de la velocidad del viento. Un "Alta" en la función usual de la presión barométrica actuaría así como una fuente (flechas saliendo), y un "Baja" será un sumidero (flechas que entran), puesto que el aire tiende a moverse desde las áreas de alta presión a las áreas de presión baja.

Véase también: Teorema de la bola peluda#Meteorología

Un campo de velocidad de un líquido móvil. En este caso, un vector de velocidad se asocia a cada punto en el líquido. En un túnel de viento, las líneas de campo se pueden revelar usando humo.

Campos magnéticos. Las líneas de campo se pueden revelar usando pequeñas limaduras de hierro.

Las ecuaciones de Maxwell permiten que utilicemos un conjunto dado de condiciones iniciales para deducir, para cada punto en el espacio euclidiano, una magnitud y una dirección para la fuerza experimentada por una partícula de prueba cargada en ese punto; el campo vectorial que resulta es el campo electromagnético.

Campo gradiente

Los campos vectoriales se pueden construir a partir de campos escalares usando el operador diferencial vectorial gradiente que da lugar a la definición siguiente.

Un campo vectorial C^k F sobre X se llama un campo gradiente o campo conservativo si existe una función C^k+1 a valores reales f: X → R (un campo escalar) de modo que

\mathbf{F}(\mathbf{x}) = \nabla f(\mathbf{x}) \qquad (\mathbf{x} \in X)

La integral curvilínea sobre cualquier curva cerrada (e.g. γ(a) = γ(b)) en un campo gradiente es siempre cero.

\oint_\gamma \langle \mathbf{F}( \mathbf{x} ), d\mathbf{x} \rangle = \int_a^b \langle \nabla f( \mathbf{\gamma} (t)), \mathbf{\gamma}'(t) \rangle \, dt = \int_a^b \frac{d}{dt} f \circ \mathbf{\gamma}(t) \, dt = f(\mathbf{\gamma}(b)) - f(\mathbf{\gamma}(a)) = 0

Campo central

Un campo vectorial C^∞ sobre Rⁿ \{0} se llama campo central si puede encontrarse un punto

\mathbf{x}_S

tal que:

$\mathbf{F}(\mathbf{O}(\mathbf{x}-\mathbf{x}_S)) = \mathbf{O}(\mathbf{F}(\mathbf{x}-\mathbf{x}_S)) \qquad (\mathbf{O} \in O(n, \mathbf{R}) \mbox{ , } \mathbf{x} \in R^n \setminus \lbrace 0 \rbrace )$

Donde O(n, R) es el grupo ortogonal.Se dice que los campos centrales son invariantes bajo transformaciones ortogonales alrededor de un punto S cuyo vector posición es

\mathbf{x}_S

. El punto S se llama el centro del campo.

Un campo central es siempre un campo gradiente, por los campos centrales pueden ser caracterizados más fácilmente mediante:

$\mathbf{F}(\mathbf{x}) = -\left(\frac{\part U}{\part x}\mathbf{\hat{i}} + \frac{\part U}{\part y}\mathbf{\hat{j}} + \frac{\part U}{\part z}\mathbf{\hat{k}}\right)$

Donde

U=f(\|\mathbf{x}-\mathbf{x}_S\|)

es una función potencial que depende sólo de la distancia entre el punto donde se mide el campo y el "centro del campo".

Campo solenoidal

Otros campos vectoriales se pueden construir a partir de un campo vectorial usando el operador diferencial vectorial rotacional que da lugar a la definición siguiente.

Un campo vectorial C^k F sobre X se llama un campo solenoidal si existe una función vectorial C^k+1 A: X → Rⁿ (un campo vectorial) de modo que:

$\mathbf{F}(\mathbf{x}) = \nabla \times \mathbf{A}(\mathbf{x}) \qquad (\mathbf{x} \in X)$

La integral de superficie o flujo cualquier superficie cerrada de un campo solenoidal es siempre cero.

$\oint_{\partial V} \langle \mathbf{F}( \mathbf{x} ), d\mathbf{S} \rangle = \int_V \nabla \cdot (\nabla \times \mathbf{A})\ dV = \int_V 0\ dV = 0$

Integral curvilínea

Una técnica común en la física es integrar un campo vectorial a lo largo de una curva. Dado una partícula en un campo vectorial gravitacional, donde cada vector representa la fuerza que actúa en la partícula en ese punto del espacio, la integral curvilínea es el trabajo hecho sobre la partícula cuando viaja a lo largo de cierta trayectoria.

La integral curvilínea se construye análogamente a la integral de Riemann y existe si la curva es rectificable (tiene longitud finita) y el campo vectorial es continuo.

Dado un campo vectorial F(x) y una curva γ(t) de a a b se define la integral curvilínea como

\int_\gamma \langle \mathbf{F}( \mathbf{x} ), d\mathbf{x} \rangle = \int_a^b \langle \mathbf{F}( \mathbf{\gamma}(t) ), \mathbf{\gamma}'(t) \rangle dt

Algunas reglas simples para el cálculo de los integrales curvilíneas son

\int_\gamma \langle (\mathbf{F} + \mathbf{G})( \mathbf{x} ), d\mathbf{x} \rangle = \int_\gamma \langle \mathbf{F}( \mathbf{x} ), d\mathbf{x} \rangle + \int_\gamma \langle \mathbf{G}( \mathbf{x} ), d\mathbf{x} \rangle

\int_\gamma \langle \alpha \cdot \mathbf{F}( \mathbf{x} ), d\mathbf{x} \rangle = \alpha \cdot \int_\gamma \langle \mathbf{F}( \mathbf{x} ), d\mathbf{x} \rangle

\int_{-\gamma} \langle \mathbf{F}( \mathbf{x} ), d\mathbf{x} \rangle = -\int_\gamma \langle \mathbf{F}( \mathbf{x} ), d\mathbf{x} \rangle

\int_{\gamma_1 + \gamma_2} \langle \mathbf{F}( \mathbf{x} ), d\mathbf{x} \rangle = \int_{\gamma_1} \langle \mathbf{F}( \mathbf{x} ), d\mathbf{x} \rangle + \int_{\gamma_2} \langle \mathbf{F}( \mathbf{x} ), d\mathbf{x} \rangle

Curvas integrales

Los campos vectoriales tienen una interpretación agradable en términos de ecuaciones diferenciales ordinarias de primer orden autónomas.

Dado un C⁰ campo vectorial F definido sobre X

\mathbf{y} = \mathbf{F}(\mathbf{x}) \qquad (\mathbf{x} \in X)

podemos intentar definir curvas γ(t) sobre X de modo que para cada t en un intervalo I

\mathbf{\gamma}(t) = \mathbf{x} \qquad (t \in I)

\mathbf{\gamma}'(t) = \mathbf{y} \qquad (t \in I)

Puesto en nuestra ecuación de campo vectorial conseguimos

\mathbf{\gamma}'(t) = \mathbf{F}(\mathbf{\gamma}(t)) \qquad (t \in I)

lo que es la definición de una ecuación diferencial ordinaria de primer orden explícita con las curvas γ(t) como soluciones.

Si F es Lipschitz continua se puede encontrar una curva C¹ única γ_x para cada punto x en X de modo que

\mathbf{\gamma}_x(0) = \mathbf(x)

\mathbf{\gamma}'_x(t) = \mathbf{F}(\mathbf{\gamma}_x(t)) \qquad ( t \in (-\epsilon, +\epsilon) \subset \mathbb{R})

Las curvas γ_x se llaman las curvas integrales del campo vectorial F y particionan X en clases de equivalencia. No es siempre posible ampliar el intervalo (-µ, +µ) a la recta real total. El flujo puede por ejemplo alcanzar el borde de X en un tiempo finito.

Integrar el campo vectorial a lo largo de cualquier curva integral γ da

\int_\gamma \langle \mathbf{F}( \mathbf{x} ), d\mathbf{x} \rangle = \int_a^b \langle \mathbf{F}( \mathbf{\gamma}(t) ), \mathbf{\gamma}'(t) \rangle dt = \int_a^b dt = \mbox{constante}.

En dimensión 2 o tres se puede visualizar el campo vectorial como dando lugar a un flujo en X. Si dejamos caer una partícula en este flujo en el punto x se moverá a lo largo de una curva γ_x en el flujo dependiendo del punto inicial x. Si x es un punto estacionario en F entonces la partícula seguirá estacionaria.

Los usos típicos son aerodinámica en líquidos, flujo geodésico, los subgrupos uniparamétricos y la función exponencial en grupos de Lie.

Teorema de Poincaré

El teorema de Poincaré sobre 1-formas exactas tiene varias consecuencias interesantes para los campos vectoriales:

Si un campo vectorial cumple en algún punto P que $\boldsymbol\nabla \times \mathbf{A} = 0$ , entonces el campo es localmente conservativo, es decir, existe un entorno de P donde se cumple que: $\mathbf{A} = \boldsymbol\nabla \phi$ , es decir, es localmente expresable como el gradiente de un campo escalar.
Si un campo vectorial es solenoidal en un punto P: $\boldsymbol\nabla \cdot \mathbf{A} = 0$ , entonces el campo localmente deriva de un potencial vector, es decir, existe un entorno de Pdonde se cumple que: $\mathbf{A} = \boldsymbol\nabla \times \mathbf{P}$ .