Conjunto de nivel
Sea  un conjunto y
un conjunto y  un campo escalar sobre
un campo escalar sobre  . El conjunto de nivel
. El conjunto de nivel 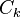 para la función
para la función  es el subconjunto de puntos
es el subconjunto de puntos  en
en  para los cuales
para los cuales  .
.
 un conjunto y
un conjunto y  un campo escalar sobre
un campo escalar sobre  . El conjunto de nivel
. El conjunto de nivel 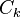 para la función
para la función  es el subconjunto de puntos
es el subconjunto de puntos  en
en  para los cuales
para los cuales  .
.
En símbolos:
Un conjunto de nivel puede coincidir con el conjunto vacío.
- Si
 los conjuntos de nivel son en general curvas y se las llama curvas de nivel.
los conjuntos de nivel son en general curvas y se las llama curvas de nivel. - Si
 los conjuntos de nivel suelen ser superficies y se les llama superficies de nivel.
los conjuntos de nivel suelen ser superficies y se les llama superficies de nivel. - Para dimensiones mayores, no se cuenta con una representación gráfica de estos conjuntos
Aplicaciones
- En cartografía, las curvas de nivel unen los puntos de un mapa que se encuentran a la misma altura (cota). Cuando representan los puntos de igual profundidad en el océano y en el mar, así como en lagos de grandes dimensiones, se denominan isóbatas
- En meteorología, las curvas de nivel se suelen usar para unir puntos que tienen la misma presión (isobaras).
- En electromagnetismo, las curvas o superficies de nivel pueden representar conjuntos que tienen un mismo potencial.
Conjuntos de nivel y gradientes
Si el conjunto  coincide con
coincide con  y el campo escalar
y el campo escalar  es de clase
es de clase  entonces los vectores gradiente del campo escalar son ortogonales a los conjuntos de nivel en el siguiente sentido: Sea
entonces los vectores gradiente del campo escalar son ortogonales a los conjuntos de nivel en el siguiente sentido: Sea 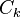 un conjunto de nivel y
un conjunto de nivel y  una curva diferenciable. Los vectores gradiente del campo
una curva diferenciable. Los vectores gradiente del campo  sobre la curva, son ortogonales a los vectores velocidad de la curva.
sobre la curva, son ortogonales a los vectores velocidad de la curva.
 coincide con
coincide con  y el campo escalar
y el campo escalar  es de clase
es de clase  entonces los vectores gradiente del campo escalar son ortogonales a los conjuntos de nivel en el siguiente sentido: Sea
entonces los vectores gradiente del campo escalar son ortogonales a los conjuntos de nivel en el siguiente sentido: Sea 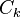 un conjunto de nivel y
un conjunto de nivel y  una curva diferenciable. Los vectores gradiente del campo
una curva diferenciable. Los vectores gradiente del campo  sobre la curva, son ortogonales a los vectores velocidad de la curva.
sobre la curva, son ortogonales a los vectores velocidad de la curva.
En efecto, para todo  en
en  ,
,
 en
en  ,
,
Derivando respecto de  se obtiene (usando la derivada de una composición de funciones)
se obtiene (usando la derivada de una composición de funciones)
 se obtiene (usando la derivada de una composición de funciones)
se obtiene (usando la derivada de una composición de funciones)
En particular, las curvas integrales asociadas al campo vectorial generado por el gradiente de  son "ortogonales" a los conjuntos de nivel asociadas a dicha función.
son "ortogonales" a los conjuntos de nivel asociadas a dicha función.
 son "ortogonales" a los conjuntos de nivel asociadas a dicha función.
son "ortogonales" a los conjuntos de nivel asociadas a dicha función.
En física, estas curvas integrales se las suele llamar líneas de campo o líneas de fuerza, según el contexto.
numerable o contable cuando sus elementos pueden ponerse en correspondencia uno a uno con el conjunto de los números naturales o un subconjunto finito del mismo.
Algunos autores toman una definición alternativa de conjunto numerable que incluye también a los conjuntos finitos. Esta definición establece que un conjunto es numerable cuando existe correspondencia uno a uno entre el conjunto y algún subconjunto de los números naturales y es por esto que en ocasiones se especificaconjunto infinito numerable o a lo sumo numerable para evitar ambigüedades, refiriendo la primera expresión únicamente a conjuntos infinitos y la segunda permitiendo conjuntos finitos.
Georg Cantor fue el primero que hizo uso de este concepto en un artículo publicado en 1874 que marcaría el nacimiento de la teoría de conjuntos.1 Sin embargo, su importancia se manifiesta en numerosos campos de las matemáticas, en particular en el análisis, en teoría de la medida y en topología.
- El conjunto de todos los números pares, es numerable porque la función:
es una biyección: cada número natural corresponde a un único número par y viceversa.
- El conjunto
 de todos los enteros también es numerable.
de todos los enteros también es numerable. - El conjunto
 es numerable.
es numerable. - Como consecuencia del ejemplo anterior, el conjunto de todos los racionales también es numerable.
- Por inducción puede probarse que
 son numerables para cualquier número natural k.
son numerables para cualquier número natural k.
Introducción
Definiciones
De manera más formal, un conjunto C se dice que es numerable cuando es equipotente con el conjunto de los números naturales  , es decir, cuando existe unabiyección de
, es decir, cuando existe unabiyección de  con C. Algunos autores extienden la definición para incluir los conjuntos finitos, y bajo esta extensión un conjunto numerable es aquel que se puede poner en biyección con un subconjunto de los números naturales. Esta extensión será designada en este artículo con la expresión «conjunto a lo sumo numerable» o «conjunto finito o numerable».2 En caso de que pueda haber ambigüedad, siempre se puede especificar que un conjunto equipotente con
con C. Algunos autores extienden la definición para incluir los conjuntos finitos, y bajo esta extensión un conjunto numerable es aquel que se puede poner en biyección con un subconjunto de los números naturales. Esta extensión será designada en este artículo con la expresión «conjunto a lo sumo numerable» o «conjunto finito o numerable».2 En caso de que pueda haber ambigüedad, siempre se puede especificar que un conjunto equipotente con  es un «conjunto infinitonumerable».
es un «conjunto infinitonumerable».
 , es decir, cuando existe unabiyección de
, es decir, cuando existe unabiyección de  con C. Algunos autores extienden la definición para incluir los conjuntos finitos, y bajo esta extensión un conjunto numerable es aquel que se puede poner en biyección con un subconjunto de los números naturales. Esta extensión será designada en este artículo con la expresión «conjunto a lo sumo numerable» o «conjunto finito o numerable».2 En caso de que pueda haber ambigüedad, siempre se puede especificar que un conjunto equipotente con
con C. Algunos autores extienden la definición para incluir los conjuntos finitos, y bajo esta extensión un conjunto numerable es aquel que se puede poner en biyección con un subconjunto de los números naturales. Esta extensión será designada en este artículo con la expresión «conjunto a lo sumo numerable» o «conjunto finito o numerable».2 En caso de que pueda haber ambigüedad, siempre se puede especificar que un conjunto equipotente con  es un «conjunto infinitonumerable».
es un «conjunto infinitonumerable».
Por el contrario, un conjunto (infinito) no numerable es un conjunto infinito que no es equipotente con  . El argumento de la diagonal de Cantor permite demostrar que el conjunto de los números reales
. El argumento de la diagonal de Cantor permite demostrar que el conjunto de los números reales  y el conjunto de las partes de
y el conjunto de las partes de  no son numerables, y asimismo muestra la existencia de numerosos infinitos distintos de los anteriores y que tampoco son numerables.
no son numerables, y asimismo muestra la existencia de numerosos infinitos distintos de los anteriores y que tampoco son numerables.
 . El argumento de la diagonal de Cantor permite demostrar que el conjunto de los números reales
. El argumento de la diagonal de Cantor permite demostrar que el conjunto de los números reales  y el conjunto de las partes de
y el conjunto de las partes de  no son numerables, y asimismo muestra la existencia de numerosos infinitos distintos de los anteriores y que tampoco son numerables.
no son numerables, y asimismo muestra la existencia de numerosos infinitos distintos de los anteriores y que tampoco son numerables.Teorema de Cantor
Un conjunto que contiene un subconjunto infinito numerable es necesariamente infinito. A partir de los axiomas de la teoría de conjuntos, en particular el axioma de elección, se puede mostrar que el infinito numerable es el infinito más pequeño en el sentido de que todo conjunto infinito contiene un conjunto infinito numerable. Se puede entonces caracterizar un conjunto infinito como un conjunto que contiene un subconjunto numerable, definición que tiene aplicaciones en teoría de la cardinalidad.
El cardinal de  , y por tanto el cardinal de cualquier conjunto numerable, se denota
, y por tanto el cardinal de cualquier conjunto numerable, se denota  (alef cero). Es el primero de los ordinales transfinitos álef, que representan todos los cardinales dado el axioma de elección.
(alef cero). Es el primero de los ordinales transfinitos álef, que representan todos los cardinales dado el axioma de elección.
 , y por tanto el cardinal de cualquier conjunto numerable, se denota
, y por tanto el cardinal de cualquier conjunto numerable, se denota  (alef cero). Es el primero de los ordinales transfinitos álef, que representan todos los cardinales dado el axioma de elección.
(alef cero). Es el primero de los ordinales transfinitos álef, que representan todos los cardinales dado el axioma de elección.Origen del término
La noción de numerabilidad fue introducida por Georg Cantor en un artículo de 1874,3 Sobre una propiedad del sistema de todos los números algebraicos reales4donde establece por una parte que el conjunto de números algebraicos reales (es decir, el conjunto de los números reales que son solución de alguna ecuación polinómica con coeficientes enteros) es numerable,5 y por otra que el conjunto de todos los números reales no lo es, a partir de lo cual deduce inmediatamente la existencia de números trascendentes o no algebraicos, redescubriendo así un resultado de Liouville.
Su origen está ligado a la concepción del infinito en matemáticas. Hasta el descubrimiento de Cantor, el infinito era el infinito potencial, la posibilidad de continuar un proceso sin detenerse nunca. La comparación de conjuntos infinitos trae consigo la noción de infinito alcanzado, actual o completo: un conjunto infinito visto como un todo, un concepto que ha sido rechazado por numerosos matemáticos (Gauss, o, en la época de Cantor, Kronecker, etc).6 Para ellos, el hecho de considerar una infinidad de objetos como un todo, es decir, el concepto de conjunto infinito, no tiene sentido, sino que el infinito sólo puede surgir del proceso de enumeración sin repetición que nunca se detiene. Sólo el infinito numerable puede tener en rigor algún sentido.
CONJUNTOS FINITOS E INFINITOS NUMERABLES
Definición:
El tamaño de un conjunto es la cantidad de elementos distintos del conjunto.
Ejemplos:El tamaño de un conjunto es la cantidad de elementos distintos del conjunto.
a) El tamaño del conjunto {a, b, c} es 3
b) El tamaño del conjunto {a, o, d} es 3
c) El tamaño del conjunto {{a, b}} es 1
d) El tamaño del conjunto  es cero
es cero
Para encontrar el tamaño de dos conjuntos de manera comparativa, se necesita la siguiente
Definición:Dados dos conjuntos P y Q se dice que existe una correspondencia uno a uno (Biunicova) entre los elementos de P y los de Q, si es posible “aparear” los elementos de P y de Q de tal modo que todos los elementos P estén aparecidos con distintos elementos de Q.
Ejemplo:
Existe una correspondencia biunívoca entre los elementos de {a, b} y los de {c, d}, también existe una correspondencia biunívoca entre los de {a, b, c} y los de {0, a, b}, pero no existe una correspondencia biunívoca entre los elementos de {a, b, c} y los de {a, d}.
Definición:
Se dice que un conjunto es finito si existe una correspondencia biunívoca entre los elementos del conjunto y los elementos de algún conjunto n
Ejemplo:
La cardinalidad de los conjuntos {a, b, c}, {a, o, d}, {1, 2, 3}, {
Definición:
Se dice que un conjunto es infinito contable (o inifito numerable o que la cardinalidad del conjunto es infinita contable), si existe una correspondencia uno a uno entre los elementos del conjunto y los elemento de
Ejemplos:
El conjunto de los números naturales
El conjunto de todos los enteros pares no negativos { 2, 4, 6, ...}es un conjunto infinito contable, pues existe una correspondencia uno a uno entre los enteros pares no negativos y los números naturales, a saber el entero 2i le corresponde el número natural i, para i = 1, 2, ..., es decir:
De manera análoga, el conjunto de todos múltiplos de 7 no negativos {7, 14, 21, ... }es infinitos numerable, es decir:
Cabe señalar que un conjunto es infinito contable si, comenzando con un cierto elemento podemos listar sucesivamente, uno detrás de otro todos los elementos del conjunto, pues esa lista nos permite construir una correspondencia uno a uno entre los elementos del conjunto y los números naturales  .
.
Ejemplo:
El conjunto de los enteros
La unión de un número finito contable de conjuntos infinitamente contable es un conjunto infinito contable. Lo mismo sucede con la unión de un número infinito contable de conjuntos infinitos contables.
Ejemplo:
El conjunto de los números racionales es un conjunto infinito numerable ya que puede ser listado como sigue:
es un conjunto infinito numerable ya que puede ser listado como sigue:
El conjunto de los números racionales
Además se puede observar que se pueden hacer una cantidad infinita numerable de sublistas, donde cada una es a la vez un conjunto infinito numerable, y la unión de todas ellas es el conjunto de los números racionales  .
.





No hay comentarios:
Publicar un comentario