miércoles, 14 de octubre de 2015

Análisis matemático


combinación convexa es una combinación lineal de puntos (los cuales pueden ser vectores, escalares o más en general puntos en un espacio afín) donde todos los coeficientes son no negativos y suman 1. Todas las posibles combinaciones convexas están dentro de la envoltura convexa de los puntos dados. De hecho, la colección de todas la combinaciones convexas de puntos en el conjunto constituye la envoltura convexa del conjunto.
Formalmente, dando un conjunto finito de puntos x_1,x_2,\dots,x_n en un espacio vectorial real, una combinación convexa de esos puntos es un punto de la forma
\alpha_1 x_1+\alpha_2 x_2 + \dots + \alpha_n x_n
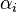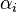donde los numero reales \alpha_i satisface \alpha_i\geq 0 y \alpha_1+\alpha_2+\dots+\alpha_n=1

Dados tres puntos x_1, x_2, x_3 en el plano como se muestra en la figura, el punto P es combinación convexa de los tres puntos, mientras que Q no lo es.
(Q es sin embargo una combinación afín de los tres puntos, así como suenvoltura afín es todo el plano.)


El análisis de la convexidad de conjuntos así como los diferentes tipos de convexidad o concavidad de funciones son instrumentos fundamentales para la Teoría de la Optimización Matemática.
Es necesario por tanto estudiar el comportamiento de este tipo de conjuntos. Por ello en este apartado vamos a analizar la definición de conjunto convexo así como el estudio de sus propiedades fundamentales.

Concepto de conjunto convexo.
Para analizar el concepto de conjunto convexo vamos a plantea el siguiente ejemplo.
 
 
EJEMPLO.
Consideremos los siguientes CONJUNTOS:
CONJUNTO A
CONJUNTO B
CONJUNTO C
CONJUNTO D.

Definimos la idea de conjunto convexo como aquel conjunto que contiene cualquier segmento que une dos puntos del conjunto.
Así por ejemplo según esta idea GRAFICA, el conjunto A

Obsérvese que para cualquier par de puntos (x,y) que estén dentro del conjunto A, el segmento que une dichos puntos siempre queda dentro del conjunto, en consecuencia A sería un conjunto convexo.
Consideremos el conjunto B:
Obsérvese que para cualquier par de puntos (x,y) que estén dentro del conjunto B, el segmento que une dichos puntos no queda dentro del conjunto, en consecuencia B no sería un conjunto convexo.
Consideremos el conjunto C:
 
En este caso para cualquier par de puntos (x,y) de esta recta C, el segmento que los une queda dentro del conjunto, en consecuencia C es un conjunto convexo.
Por último sea el conjunto D:

Es claro gráficamente que para cualquier par de puntos x, y, el segmento que los une está totalmente contenido en dicho conjunto.
Consideremos un último ejemplo en el plano, sea el conjunto E
 
(conjunto poligonal delimitado por los puntos (0,0),(5,0),(0,3),(1,2),(0,0) )
Se puede ver que existen segmentos, como el indicado en la figura que se sale del conjunto por lo que este conjunto no sería CONVEXO.

EJERCICIO VII-1
Determinar si los siguientes conjuntos son o no convexos, dibujandoles previamente:
  1. Conjunto poligonal determinado por los puntos (0,1),(1,0),(1,3),(0,1)
  2. Conjunto poligonal determinado por los puntos (1,1),(2,1),(2,3),(-1,2),(-1,0),(1,1)
SOLUCION:
  1. es convexo
(b) no es convexo
Podemos definir conjuntos en el plano de una manera más compleja:
Así por ejemplo si consideramos el conjunto
 

¿Qué hacemos para dibujar este conjunto?

Primero dibujamos la curva que delimita el conjunto. En DERIVE resulta sencillo basta editar la función y=x y aplicar Plot
Para delimitar la región del plano basta considerar un punto que no esté en la curva, por ejemplo (1,2) si ese punto satisface la ecuación entonces ese es el recinto a considerar, en nuestro caso como 2 sí es mayor o igual que 1, entonces el recinto es
 
Obsérvese que es claramente convexo pues cualquier par de puntos que estén en S3 el segmento que los une está claramente contenido en S3.
¿Qué sucedería si no podemos representar gráficamente el conjunto, como sucede con conjuntos de dimensión superior a 3?
En esos casos es necesario dar una definición analítica de conjunto convexo, para lo cual efectuamos la siguiente definición:
 
CONJUNTO CONVEXO.
Diremos que un subconjunto SÍ Rn es convexo si para cualquier par de puntos  y para cualquier lΠ[0,1] se cumple que   está en S,es decir que si llamaMos segmento de extremos  por
S es convexo si para cualesquiera , 
 
 
¿cuál es el significado de z=l x+(1-l )y?
Vamos a verlo en un ejemplo:
EJEMPLO:
Estudiar analíticamente si el conjunto anterior
es un conjunto convexo.
Para ello consideremos dos vectores de S3
(x1,y1), (x2,y2),
Habría que comprobar si b(x1,y1)+(1-b)(x2,y2) es un vector que pertenece a S3 para cualquier valor de b en [0,1]
Es decir tendremos que comprobar si
.bx1+(1-b)x2 ³ by1+(1-b)y2
Como x1³y1 entonces bx1³by1 (pues b es positivo o cero)
Y como x2³y2 entonces (1-b)x2³(1-b)y2
Sumando ambas expresiones se obtiene la desigualdad por tanto S3 es un conjunto convexo.
Esto en DERIVE se puede realizar definiendo dos vectores:
Y comprobando si el vector
Que una vez simplificado nos da
Y al expandirle
Si es un vector del conjunto S3. 
 
EJERCICIO VII-2
Estudiar de forma gráfica si los siguientes conjuntos son o no conjuntos convexos.
SOLUCIONES:
  1. Lo hacemos gráficamente, representando el conjunto.

    2. Para ello dibujamos los dos límites del conjunto x2+y2=1 y x2+y2=4 (circunferencias de radio 1 y radio 2)Definimos las expresiones
    Y luego las representamos con el comando Plot.

    ¿cuál es el recinto?
    Ahora debemos determinar en que lado de la circunferencias se situa el conjunto.
    Tomemos un punto fuera de ambas circunferencias, por ejemplo (0,0),. Y comprobemos si se verifica la primera desigualdad para ese punto

    Efectivamente no se verifica, por tanto el conjunto se situa hacia fuera de la circunferencia.
    Por otro lado


    Es cierta por tanto el conjunto es la corona circular situada entre la circunferencia de radio 1 y la circunferencia radio 2.
    ¿Este conjunto es convexo?
    Claramente se ve que no, tomemos dos puntos cualesquiera por ejemplo (-1,1/2) y (2,0), ambos pertenecen al conjunto, sin embargo el segmento que los une como se ve no pertenecen al conjunto.
  2. Consideremos las expresiones que definen los límites del conjunto:
Representemos ambas rectas: 
 

Para saber cuál es exactamente el recinto, tomemos un punto que no esté en dichas rectas, por ejemplo (0,0).
Comprobemos a qué lado de la recta x+y=1 se encuentra nuestro conjunto x+y£ 1, comprobamos para (0,0), y observamos que 0+0£ 1 verifica la ecuación, por tanto el recinto x+y£ 1 está al lado del (0,0) .
 

Y por otro lado para determinar el conjunto x-y£ 1 comprobamos que 0-0£ 1 por tanto tambien es de la recta hacia el (0,0), con lo cual tendremos que el recinto será:
 

EJERCICIO VII-3
Demostrar de forma analítica que el conjunto
conjunto convexo. 
 
OBSERVACIÓN.
En general si  es un vector de Rn cΠR se verifica que los conjuntos:
H={ΠRn/ t. =c}
H+={ΠRn/ t . ³ c} H-={ΠRn/ t. £ c}
H0+={ΠRn/ t . >c} H0-={ΠRn/ t. 
Son conjuntos convexos.
Demostración
Demostremos uno de ellos por ejemplo que H={ΠRn/ t. =c} es convexo.
Sean dos vectores cualesquiera  hay que demostrar que si lΠ[0,1] entonces el vector  pertenece a H.
Si  entonces se verifica que ,
Si  entonces se verifica que ,
Veamos qué ocurre con el producto
 

Luego efectivamente el vector cumple la propiedad por tanto pertenece a H.
Lo mismo se puede hacer con el resto de conjuntos.
 

PROPIEDADES DE LOS CONJUNTOS CONVEXOS.
Vamos a estudiar qué sucede con la UNIÓN y la INTERSECCIÓN de conjuntos convexos. Comendemos con la INTERSECCIÓN de conjuntos convexos.
INTERSECCIÓN DE CONJUNTOS CONVEXOS.
EJEMPLO.
Sean los siguientes conjuntos convexos:

Si los representamos tendremos:
 

¿Cuál es la intersección de estos dos conjuntos?
Se puede ver que la intersección es el conjunto
 

Se puede ver gráficamente que es un conjunto convexo.
Y este ejemplo se puede generalizar con la siguiente propiedad:
LA INTERSECCIÓN DE CONJUNTOS CONVEXOS ES UN CONJUNTO CONVEXO:
Demostración:
Si Xi es un conjunto convexo para i=1,...,n. Esto quiere decir que dados dos puntos cualesquiera de este conjunto  entonces el segmento que los une está totalmente contenido en el conjunto Xi, es decir  luego esto quiere decir que  con lo que queda demostrado.
UNIÓN DE CONJUNTOS CONVEXOS.
A partir de los conjuntos convexos anteriores S y T, veamos cuál es el conjunto unión.
 

Este conjunto no es convexo pues si considero dos puntos del conjunto por ejemplo
(1.04, -1.57) y (2.43,-0.3)
Si representamo el segmento que une dichos puntos editando

Obtenemos
 

Segmento que no está totalmente contenido en el conjunto. Luego:
LA UNION DE CONJUNTOS CONVEXOS EN GENERAL NO ES UN CONVEXO
Vamos a introducir ahora dos nuevos conceptos el concepto de punto extremo de un convexo y el concepto de combinación lineal convexa:

CONCEPTO DE PUNTO EXTREMO DE UN CONVEXO.
Consideremos el siguiente conjunto convexo:
 
Para representarlo dibujamos las rectas que delimitan los conjuntos:
Vamos ahora a ir delimitando los semiplanos determinados por cada una de las desigualdades:
0£ x£ 1
Este recinto es clara su representación:

Vamos a delimitar los otros dos:   2-x£ y
Consideremos un punto que no está en la recta por ejemplo (0,0). (0,0) verifica la desigualdad?
¿2-0£ 0? No es cierto por tanto al otro lado del (0,0) es decir
 

Por último vamos a delimitar el recinto de la desigualdad y£ 2+x
De nuevo consideremos un punto que no está en la recta y=2+x como es el (0,0), ¿(0,0) satisface la desigualdad? ¿0 £ 2+0? Como es cierto entonces el semiplano está situado de la recta hacia el (0,0), es decir
 

En consecuencia el conjunto delimitado es:
 

¿Cuáles son los VERTICES de este conjunto?
La intersección de rectas:
Da el punto
Las rectas
El punto
Y las rectas
El punto
Luego los vértices de este conjunto serán:
(0,2), (1,1) y (1,3), también llamados puntos extremos de S. 
  
 
Para dar la definición más formal de PUNTO EXTREMO de un conjunto convexo, vamos a definir el concepto de COMBINACIÓN LINEAL CONVEXA.
 

DEFINICIÓN: COMBINACIÓN LINEAL CONVEXA.
Diremos que  es una combinación lineal convexa de  si existen  tales que:
Según el ejemplo anterior, podemos comprobar que TODAS LAS COMBINACIONES LINEALES CONVEXAS de los puntos (0,2), (1,3), (1,1) son todos los puntos del triangulo definido antes. Si queremos comprobar esto vamos a realizar algunas combinaciones lineales convexas de estos tres puntos.
Lo vamos a hacer con DERIVE:
Definamos en primer lugar los puntos

Vamos a ir realizando combinaciones lineales convexas y vamos a ir representando los puntos obtenidos:

 
Obsérvese que en esta caso la combinación lineal convexa da el propio p1.
En este caso p2
Y en este caso p3.
Pero existen otras formas de realizar combinaciones lineales convexas: 
 
Veamos lo que tenemos representado hasta ahora:
Continuemos haciendo combinaciones lineales convexas
 

Obtendremos las representaciones:
 
A partir de estas combinaciones lineales convexas podemos obtener una definición de punto extremo de un conjunto convexo, de la siguiente forma.
¿Cuál es la combinación lineal convexa mediante la cual obteníamos:
¿p1?
¿y p2?
¿y p3?
¿Tiene alguna característica especial?
Como puede verse estos puntos tienen una característica expecial y es que tan solo intervienen en la combinación lineal el propio punto, por ello definimos:
 
DEFINICION Punto extremo de un conjunto convexo:
Sea S un conjunto convexo. Diremos que  es un PUNTO EXTREMO de S si  no se puede expresar como combinación lineal convexa de dos puntos distintos del propio .
También se les suele llamar VERTICES del conjunto (si es en R2 ó R3).
 
EJERCICIO VII-4
Calcular los puntos extremos de los conjuntos:
SOLUCIÓN: 
(A)
(b)
Para obtener puntos extremos hay que resolver la intersección entre recta y circunferencia
Como x=1+y, entonces sustituyendo este valor de x en la circunferencia tenemos:
Resolviendo ahora obtenemos:
Luego los puntos son para y=0, x=1 (1,0)
Y para y=.-1, x=0 (0,-1) que son los puntos extremos.
Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)