Diagramas

Diagramas epónimos

diagrama de Linus Pauling (o diagrama de Pauling) es un diagrama realizado por el químico estadounidense Linus Carl Pauling para ayudar en la distribución de los electrones en los subniveles de la electrosfera.

Subniveles

Los subniveles se designan por letras: s (agudo = fuerte), p (principal), d (difuso), f (fundamental), g, h e i, siendo estos 3 últimos ausentes en el diagrama convencional, porque aunque existen en teoría, no hay átomo que tenga espacio para tantos electrones , y entonces es necesario el uso de estos subniveles.

• La capa K se compone del subnivel s.
• La capa L se compone de los subconjuntos s y p.
• La capa M se compone de los subniveles s, p y d.
• La capa N se compone de los subniveles s, p, d y f.
• La capa O se compone de los subniveles s, p, d, f y g.
• La capa P se compone de los subniveles s, p, d, f, g y h.
• La capa Q consiste en la subniveles s, p, d, f, g, h e i

Los subniveles soportan un máximo de:

• s - 2 electrones.
• p - 6 electrones.
• d - 10 electrones.
• f - 14 electrones.
• g - 18 electrones.

Correspondería a:

• K 1s2
• L 2S2 2P6
• M 3s2 3p6 3d10
• N 4D10 4S2 4p6 4f14
• El 5p6 5d10 5f14 5S2
• P 6s2 6p6 6d10
• Q 7p6 7S2
• R 8s2 8p6 7d10 6f14 5g18

diagramas de Venn son esquemas usados en la teoría de conjuntos, tema de interés en matemática, lógica de clases yrazonamiento diagramático. Estos diagramas muestran colecciones (conjuntos) de cosas (elementos) por medio de líneas cerradas. La línea cerrada exterior abarca a todos los elementos bajo consideración, el conjunto universal U.

Introducción

Con los diagramas de Venn es posible representar las relaciones de intersección, inclusión y disyunción sin cambiar la posición relativa de los conjuntos

Intersección

Dado que los conjuntos pueden tener elementos comunes, las regiones encerradas por sus líneas límite se superponen. El conjunto de los elementos que pertenecen simultáneamente a otros dos es la intersección de ambos.¹

A = {1; 2; 3; 4; 6; 12} B = {1; 3; 5; 15} U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16}
A = {x | x es divisor natural de 12} B = {x | x es divisor natural de 15} U = {x | x es natural menor o igual que 16}

Inclusión

Si todos los elementos de un conjunto son parte de los elementos de otro, se dice que el primero es un subconjunto del segundo o que está incluido en el segundo.¹ En los diagramas de Venn, todas las regiones de superposición posibles deben ser representadas. Y, cuando hay regiones que no contienen elementos (regiones vacías), la situación se indica anulándolas (con un color de fondo distinto).²

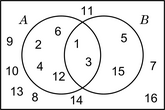
A = {1; 2; 3; 4; 6; 12} B = {1; 2; 3; 6} U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}
A = {x | x es divisor natural de 12} B = {x | x es divisor natural de 6} U = {x | x es natural menor o igual que 12}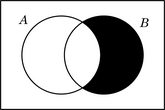

Disyunción

Cuando los conjuntos no tienen elementos comunes, la región de superposición queda vacía.

A = {2; 4; 6; 8} B = {1; 3; 5; 7; 9} U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10}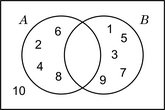
A = {x | x es par y de una cifra} B = {x | x es impar y de una cifra} U = {x | x es natural menor o igual que 10}

A la izquierda de los diagramas, las definiciones de los conjuntos por enumeración y por comprensión.

Orígenes e historia

Vitral del comedor del Caius College (Cambridge) en homenaje a John Venn y su creación

Los diagramas de Venn tienen el nombre de su creador, John Venn, matemático y filósofo británico.³ Estudiante y más tarde profesor del Caius College de la Universidad de Cambridge, Venn desarrolló toda su producción intelectual en ese ámbito.⁴

Los diagramas que hoy conocemos fueron presentados en julio de 1880 en el trabajo titulado De la representación mecánica y diagramática de proposiciones y razonamientos,⁵ que tuvo gran repercusión en el mundo de la lógica formal. Los diagramas de Venn tienen varios antecedentes. La primera representación gráfica de deducciones lógicas —y, en particular, de silogismos— se atribuye comúnmente a Gottfried Leibniz. Variantes de la misma fueron empleadas luego por George Boole y Augustus De Morgan, pero fue el gran matemático suizo Leonhard Euler quien primero introdujo una notación clara y sencilla.² El siguiente diagrama muestra de otro modo la relación de inclusión del ejemplo dado en la introducción.

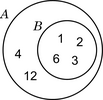diagrama de Euler

Los diagramas de Euler se distinguen de los de Venn en dos aspectos:

• en ellos no aparecen las regiones vacías y
• el conjunto universal no se representa.

Si bien fue Venn quien introdujo la expresión "universo del discurso", él nunca representó al universal en sus trabajos.³ Por eso la idea de conjunto universal se atribuye habitualmente a Charles Dodgson, más conocido como Lewis Carroll, el lógico y autor de cuentos para niños que popularizó el concepto de conjunto complementario.¹ El conjunto universal fue cuestionado porBertrand Russell, quien mostró que con tal concepto la teoría de conjuntos resultaba inconsistente (véase paradoja de Russell). Sin embargo, dicha definición fue rescatada y aun justificada en una reciente extensión de los diagramas de Venn que distingue al universal del Todo (universo del discurso).⁶ Por las dos razones recién mencionadas, los diagramas de Venn llegaron a convertirse en el nuevo estándar para la formalización de operaciones lógicas y los sistemas de representación anteriores cayeron en desuso.²

Tiempo después de la aparición del primer artículo, Venn desarrolló algo más su nuevo sistema en el libro Lógica simbólica, publicado en 1881 y cuyo propósito era interpretar y revisar los trabajos de Boole en el campo de la lógica formal. Este libro sirvió sobre todo para presentar ejemplos del uso de los diagramas.⁷ Otro libro de Venn que ayudó a divulgar el nuevo sistema de representación fue el titulado Los principios de la lógica empírica o inductiva, publicado en 1889.⁸

La primera constancia escrita del uso de la expresión "diagrama de Venn" es muy tardía (1918) y se encuentra en el libro A Survey of Symbolic Logic de Clarence Irving Lewis.⁹

Diagramas de Venn de enunciados

Como se mostró en la introducción, los diagramas de Venn pueden ser definidos por enumeración de sus elementos o por indicación de una característica común que los identifica unívocamente.¹ De ahí que haya dos tipos de diagramas de Venn: los que muestran elementos reunidos por líneas cerradas y los que simplemente muestran enunciados o conceptos. Estos últimos son más interesantes porque permiten operar de manera abstracta y llegar a conclusiones más generales.¹⁰

Los siguientes diagramas del segundo tipo muestran los resultados de cuatro operaciones básicas con conjuntos usando el código del semáforo de dos colores.¹¹

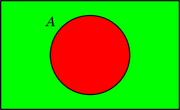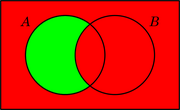¬A	A ∧ B	A ∨ B = ¬((¬A) ∧ (¬B))	A – B = A ∧ (¬B)

Como se desprende de las igualdades, con las dos primeras operaciones (negación y conjunción), es posible hacer las otras dos (disyunción y sustracción).

El código de dos colores puede ser interpretado en el sistema binario de numeración: rojo = 0; verde = 1. A los resultados de las operaciones se los puede entonces digitalizar. Y a los términos que participan de las operaciones, también. De este modo, las operaciones con conjuntos se convierten en operaciones con números.¹²

Diagramas de Venn y cantidad de definiciones

Los siguientes diagramas muestran la cantidad de regiones en que queda dividido el conjunto universal con una, dos y tres definiciones.

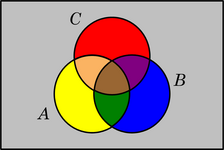1 conjunto (2 colores)	2 conjuntos (4 colores)	3 conjuntos (8 colores)

Entre los colores se cuenta el gris, que en todos los casos corresponde a los elementos que no caen en ninguna definición.

Diagrama de un conjunto

Tiene sólo 2 regiones: la de los elementos que responden a la definición A y la de los que se oponen a ella.¹

Diagrama de dos conjuntos

Tiene 4 regiones. Considérese el siguiente ejemplo: el conjunto A es el de los animales bípedos y el conjunto B es el de los animales que pueden volar. El área donde las dos regiones se superponen contiene por lo tanto a todos los animales que, al mismo tiempo, son bípedos y pueden volar. En resumen:

• A (regiones amarilla y verde): animales bípedos,
• B (regiones azul y verde): animales que pueden volar,
• A y B (región verde): animales bípedos que pueden volar,
• A y no B (región amarilla): animales bípedos que no pueden volar,
• no A y B (región azul): animales no bípedos (que no tienen dos patas) que pueden volar,
• no A y no B (región gris): animales no bípedos que no pueden volar,
• A o B (regiones amarilla, azul y verde): animales bípedos o que pueden volar.

Los pingüinos, que tienen dos patas y no pueden volar, están en la región amarilla; los mosquitos, que tienen seis patas y pueden volar, están en la región azul; los loros, que tienen dos patas y pueden volar, están en la región verde; las ballenas, que no tienen patas ni pueden volar, están en la región gris.

Diagrama de tres conjuntos

Tienen 8 regiones. Los diagramas de tres conjuntos fueron los más usados por Venn en toda su obra. Un ejemplo de aplicación podría ser el siguiente: dado un grupo de personas, A es el conjunto de las de sexo masculino, B el conjunto de las mayores de 18 años y C el conjunto de las que trabajan. De este modo, la región verde sería la de las personas de sexo masculino, mayores de 18 años, que no trabajan.¹³

Diagramas de más de tres conjuntos

La dificultad de representar más de tres conjuntos mediante diagramas de Venn es evidente. Venn sentía afición por los diagramas de más de tres conjuntos, a los que definía como "figuras simétricas, elegantes en sí mismas". A lo largo de su vida, diseñó varias representaciones usando elipses, y dejó indicaciones para la construcción de diagramas con cualquier cantidad de curvas, partiendo del diagrama de tres círculos.¹⁴

Diagramas de Edwards

Anthony William Fairbank Edwards propuso diagramas para más de tres conjuntos, proyectando el diagrama sobre una esfera. Tres conjuntos pueden ser representados fácilmente tomando tres hemisferios en ángulos rectos (x = 0, y = 0 y z = 0). Un cuarto conjunto puede ser representado tomando una curva similar a la juntura de una pelota de tenis que suba y baje alrededor del ecuador. Los conjuntos resultantes pueden ser proyectados de nuevo sobre el plano para mostrar diagramas de tipo engranaje, con cantidades cada vez mayores de dientes. Edwards ideó estos diagramas mientras diseñaba la ventana acristalada en memoria de Venn que hoy adorna el comedor del Caius College.¹⁵

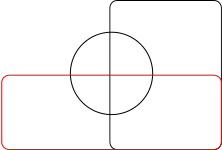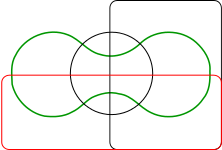3 conjuntos	4 conjuntos
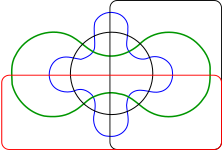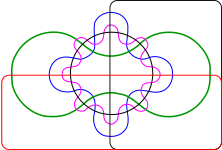5 conjuntos	6 conjuntos

Otros diagramas

Los diagramas de Edwards son topológicamente equivalentes a los diagramas diseñados por Branko Grünbaum, que se basan en la intersección de polígonos con cantidades crecientes de lados.^16 17 18 Phillip Smith ideó diagramas similares de n conjuntos usando curvas senoidales con ecuaciones del tipo y = sen(2ⁱ x)/2ⁱ, 0 ≤ i ≤ n– 2. Por su parte, Lewis Carroll diseñó un diagrama de cinco conjuntos.

Otras representaciones

A continuación se hace referencia a representaciones relacionadas con los diagramas de Venn.

Líneas de Leibniz

Las líneas de Leibniz fueron las primeras representaciones de conceptos lógicos. Leibniz también representó los conceptos con círculos, pero prefería las líneas.

Círculos de Euler

Los círculos de Euler preceden históricamente a los diagramas de Venn y en algunas aplicaciones son todavía usados.

La diferencia entre los diagramas de Euler y de Venn se observa sobre todo en las relaciones de inclusión y de disyunción.

	inclusión	disyunción
Leibniz
Euler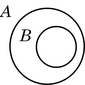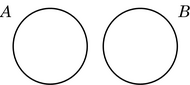
Venn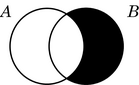

Los diagramas de Venn muestran la topología del sistema sin que sea necesario modificar la posición relativa de los conjuntos, a costa de introducir una nueva convención: el sombreado de las regiones vacías.