Finanzas

Matemática financiera

 ecuación de Fisher es una expresión que relaciona los tipos de interés nominales y reales en función de la inflación.

Recibe su nombre del economista estadounidense Irving Fisher (1867-1947).

Si  es el tipo de interés real,  el nominal y  la tasa de inflación, la ecuación de Fisher es

) = 1 +  +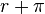 

de manera que

 + 

aunque se puede usar una útil aproximación :

ECUACIÓN DE FISHER

Una ecuación que relaciona los tipos de interés nominales con los tipos de interés reales exigidos y las tasas de inflación previstas o esperadas. Recibe su nombre de Irving Fisher, su creador. En este contexto, el término nominal significa el tipo observado en el mercado. Por ejemplo, supongamos que los prestamistas requieren un tipo real derendimiento para su dinero (es decir, un aumento neto en su poder de adquisición) del 3% anual. Al mismo tiempo, los posibles prestamistas prevén una tasa de inflación del 2%. En tal situación, el tipo de interés nominal será del 5%.

Igualdad necesaria, en una economía, entre la cantidad de dinero multiplicada por la velocidad de circulación del mismo y el nivel de precios multiplicado por el volumen de las transacciones (MV=PT). Fisher equation.

 factor de descuento (FD) o factor de actualización (FA) al coeficiente utilizado para averiguar el valor actual (presente) de cualquier flujo de caja futuro. Dicho factor de actualización va a depender tanto del tipo de interés o coste del dinero en el tiempo como del periodo de tiempo transcurrido.

En los mercados financieros el factor de descuento o factor de actualización suele calcularse a partir de la siguiente fórmula:

Donde i es el tipo de interés expresado en términos efectivos anuales y t es el tiempo en años transcurrido desde hoy hasta la fecha concreta que se desea actualizar.

Si el tipo de interés es positivo se cumple la propiedad que 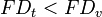 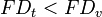si t < v. .

Los factores de descuento son necesarios para calcular, por ejemplo, el valor de un swap.

En los mercados financieros suele usarse la curva cupón cero de tipo de interés para calcular los factores de descuento.

Un factor de descuento toma una cantidadfutura de dinero y calcula su valor en el presente. En los negocios, esto se conoce como valor presente. Para calcular este factor, sólo necesitas la tasa de interés por periodo y el número de periodos. La fórmula es "1/(1+i)^t". Para cifras enteras, la tabla de valor presente de US$1 proporciona todos los factores de descuento, así que no es necesario realizar el cálculo.

 medida de neutralidad al riesgo, también llamada medida de equivalencia martingala, se utiliza para establecer precios de derivados por mor del teorema fundamental del arbitraje financiero, el cual implica que en un mercado completo el precio de un derivado es igual al valor esperado descontado del pago futuro bajo la única medida de neutralidad.

Motivando el uso de las medidas de neutralidad al riesgo

Los precios de los activos dependen crucialmente de su riesgo, porque los inversores exigen más beneficios a medida que soportan más incertidumbre. Por lo tanto, el precio actual de un contingente sobre una cantidad arriesgada el día de mañana, por lo general difieren en su valor esperado. En general, los inversores tienen aversión al riesgo y el precio de hoy está por debajo de su valor esperado, remunerando a los que asumen el riesgo. (Al menos en los grandes mercados financieros. Ejemplo de los mercados en busca de riesgo - son los casinos y las loterías.)

Para el precio de los activos, por consiguiente, los valores esperados calculados necesitan ser ajustados por las preferencias de riesgo de los inversores (véase ratio de Sharpe). Desafortunadamente, las tasas de descuento es difícil de calcular, porque varia entre las preferencias de riesgo individual y de los inversores.

modelo Arrow–Debreu (también conocido como modelo Arrow–Debreu–McKenzie) afirma que bajo determinados supuestos económicos (preferencias convexas, competencia perfecta e independencia de la demanda) debe existir un conjunto de precios tal que las ofertas agregadas sean iguales a las demandas agregadas para cada bien en la economía.¹

Este modelo es fundamental para la teoría del equilibrio general y se utiliza con frecuencia como una referencia general para otros modelos macroeconómicos. Recibe su nombre a partir de Kenneth Arrow, Gerard Debreu,² y en ocasiones también Lionel W. McKenziepor sus mejoras realizadas en 1959.³

El modelo AD es uno de los modelos más generalizados de una economía competitiva y es parte crucial de la teoría del equilibrio general, ya que puede utilizarse para probar la existencia de un equilibrio general (o equilibrio walrasiano) en una economía. En general, pueden existir múltiples equilibrios. No obstante, con supuestos adicionales sobre las preferencias del consumidor, como que sus funciones de utilidad sean fuertemente cóncavas y dos veces continuamente diferenciables, un equilibrio único existe.

En el corazón de la microeconomía actual: el modelo Arrow-Debreu.

Es en 1954 que Arrow (1921- ) y Debreu (1921- ) resuelven el problema planteado por Walras, mostrando que si las relaciones de preferencia de los consumidores, y las funciones de producción de las empresas poseen ciertas propiedades a las cuales se les puede dar un significado económico, entonces existe un sistema de precios para el cual las oferta y las demandas globales de cada bien son iguales.

El interés de esta demostración, si se les compara con iniciativas precedentes, es que se apoya exclusivamente en los comportamientos maximizadores individuales, esto es “microeconómicos”. De allí la importancia central tomado por el modelo Arrow-Debreu, denominado de competencia perfecta en la microeconomía actual. En 1959, Debreu ha publicado un libro, Teoría del valor, en el cual presenta en 100 páginas, una forma definitiva del modelo; el subtítulo es bien diciente: Un análisis axiomático del equilibrio económico, lo que es significativo del cambio de perspectiva con relación al proyecto marginalista. En efecto, Debreu no emplea por casualidad el término “axiomático”; matemático de formación y todavía de práctica, no oculta que su procedimiento consiste en deducir resultados con el empleo de las matemáticas, partiendo de axiomas, de hipótesis expresados también en forma matemática.

Como lo veremos en los dos próximos capítulos, en los cuales se examinaran en detalle las hipótesis planteadas por Arrow y Debreu, concluiremos que estas últimas no son completamente arbitrarias y se les puede dar un contenido o una interpretación de tipo económica accesible por la intuición.

Sin embargo, este contenido es de alguna manera subordinado a las necesidades de demostración matemática al punto que el economista no especializado puede legítimamente preguntarse sobre la relación entre los modelos construidos en tal perspectiva y la realidad que presumen describir. El problema del realismo de las hipótesis.

Se llega al debate sobre el “realismo de las hipótesis”, que ha hecho correr ríos de tinta y que además, está lejos de estar resuelto; en tal debate la microeconomía no está por fuera, en tanto es la rama más matematizada de la economía.

No entraremos ahora en tal discusión, en tanto nuestro propósito es explicar el procedimiento general, descifrar la significación de las hipótesis y de los resultados de los modelos, mas allá de los símbolos matemáticos o de las formulaciones aproximadas. De esta manera le daremos una particular atención a las formas de organización socialsubyacentes en tales modelos, de tal manera que el lector pueda juzgar con cierto grado de realismo.

Además, el estudio de las principales características de la competencia perfecta, objeto del próximo capítulo, nos dará la oportunidad de aplicar este principio.














 modelo de valoración de activos financieros, denominada en inglés Capital asset pricing model (CAPM) es un modelo introducido por Jack L. Treynor, William Sharpe, John Litner y Jan Mossin de forma independiente, basado en trabajos anteriores de Harry Markowitz sobre la diversificación y la Teoría Moderna de Portfolio. Sharpe, profesor de la Universidad de Stanford recibió el Premio Nobel de Economía (en conjunto con Harry Markowitz y Merton Miller, profesor de University of Chicago Booth School of Business) por su contribución al campo de la economía financiera.

Fórmula

El CAPM es un modelo para calcular el precio de un activo y pasivo o una cartera de inversiones. Para activos individuales, se hace uso de la recta stock market line (SML) (la cual simboliza el retorno esperado de todos los activos de un mercado como función del riesgo no diversificable) y su relación con el retorno esperado y el riesgo sistémico (beta), para mostrar cómo el mercado debe estimar el precio de un activo individual en relación a la clase a la que pertenece.

La línea SML permite calcular la proporción de recompensa-a-riesgo para cualquier activo en relación con el mercado general.

La relación de equilibrio que describe el CAPM es:

donde:

•  es la tasa de rendimiento esperada de capital sobre el activo .
•  es el beta (cantidad de riesgo con respecto al Portafolio de Mercado), o también

, y

•  es el exceso de rentabilidad del portafolio de mercado.
•  Rendimiento del mercado.
•  Rendimiento de un activo libre de riesgo.

Es importante tener presente que se trata de un Beta no apalancado, es decir que se supone que una empresa no tiene deuda en su estructura de capital, por lo tanto no se incorpora el riesgo financiero, y en caso de querer incorporarlo, debemos determinar un Beta apalancado; por lo tanto el rendimiento esperado será más alto.

Precio de un activo

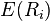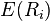Una vez que el retorno esperado, , es calculado utilizando CAPM, los futuros flujos de caja que producirá ese activo pueden ser descontados a su valor actual neto utilizando esta tasa, para poder así determinar el precio adecuado del activo o título valor.

En teoría, un activo es apreciado correctamente cuando su precio observado es igual al valor calculado utilizando CAPM. Si el precio es mayor que la valuación obtenida, el activo está sobrevaluado, y viceversa.

Retorno requerido para un activo específico

CAPM calcula la tasa de retorno apropiada y requerida para descontar los flujos de efectivo futuros que producirá un activo, dada la apreciación de riesgo que tiene ese activo. Betas mayores a 1 simbolizan que el activo tiene un riesgo mayor al promedio de todo el mercado; betas debajo de 1 indican un riesgo menor. Por lo tanto, un activo con un beta alto debe ser descontado a una mayor tasa, como medio para recompensar al inversor por asumir el riesgo que el activo acarrea. Esto se basa en el principio que dice que los inversores, entre más riesgosa sea la inversión, requieren mayores retornos.

Puesto que el beta refleja la sensibilidad específica al riesgo no diversificable del mercado, el mercado, como un todo, tiene un beta de 1. Puesto que es imposible calcular el retorno esperado de todo el mercado, usualmente se utilizan índices, tales como el S&P 500 o el Dow Jones.

Riesgo y diversificación

El riesgo dentro de un portafolio incluye el riesgo sistemático, conocido también como riesgo no diversificable. Este riesgo se refiere al riesgo al que están expuestos todos los activos en un mercado. Por el contrario, el riesgo diversificable es aquel intrínseco a cada activo individual. El riesgo diversificable se puede disminuir agregando activos al portafolio que se mitiguen unos a otros, o sea diversificando el portafolio. Sin embargo, el riesgo sistemático no puede ser disminuido.

Por lo tanto, un inversor racional no debería tomar ningún riesgo que sea diversificable, pues solamente el riesgo no diversificable es recompensado en el alcance de este modelo. Por lo tanto, la tasa de retorno requerida para un determinado activo, debe estar vinculada con la contribución que hace ese activo al riesgo general de un determinado portafolio.

Suposiciones de CAPM

El modelo asume varios aspectos sobre inversores y mercados:

1. Los individuos son aversos al riesgo, y maximizan la utilidad de su riqueza en el próximo período. Es un modelo plurianual.
2. Los individuos no pueden afectar los precios, y tienen expectativas homogéneas respecto a las varianzas-covarianzas y acerca de los retornos esperados de los activos.
3. El retorno de los activos, se distribuye de manera normal. Explicando el retorno con la esperanza matemática y el riesgo con la desviación estándar.
4. Existe un activo libre de riesgo, al cual los individuos pueden prestar y/o endeudarse en cantidades ilimitadas. El mercado de activos es perfecto. La información es gratis y está disponible en forma instantánea para todos los individuos.
5. La oferta de activos es fija.

Inconvenientes de CAPM

• El modelo no explica adecuadamente la variación en los retornos de los títulos valores. Estudios empíricos muestran que activos con bajos betas pueden ofrecer retornos más altos de los que el modelo sugiere.
• El modelo asume que todos los inversores tienen acceso a la misma información, y se ponen de acuerdo sobre el riesgo y el retorno esperado para todos los activos.
• El portafolio del mercado consiste de todos los activos en todos los mercados, donde cada activo es ponderado por su capitalización de mercado. Esto asume que los inversores no tienen preferencias entre mercados y activos, y que escogen activos solamente en función de su perfil de riesgo-retorno.