Matemática financiera

modelo de Gordon-Shapiro, también conocido como el modelo de dividendos crecientes a tasas constantes, es una variación del modelo de análisis de flujos de caja descontados, usado para avaluar acciones o empresas. Este modelo presupone un crecimiento de los dividendos a una tasa constante (g), siendo por eso un modelo aconsejado para empresas con crecimiento bajo y constante a lo largo del tiempo. Este fue publicado por primera vez en 1956 por los economistas Myron J. Gordon yEli Shapiro, de ahí el nombre del modelo.

El modelo

Para determinar el valor de la acción se considera el valor actual de los dividendos futuros más el valor actual del valor futuro de venta, tomando la tasa de ganancia requerida de los accionistas (k) como tasa de descuento.

La fórmula utilizada en el modelo Gordon-Shapiro es la siguiente:

P_0 = \frac{D_1}{k-g}

Donde:

• Po: Valor teórico de la acción.
• D: Dividendo anticipado del primer periodo.
• k: Tasa de descuento del mercado.
• g: Tasa de crecimiento de los dividendos.

Este modelo calcula el precio de la acción como el valor actual de una renta perpetua con crecimiento constante.

Propiedades del modelo

a) Cuando la tasa de crecimiento de los dividendos (g) es 0 el modelo queda de la siguiente forma:

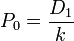P_0 = \frac{D_1}{k}

Por lo que si despejamos tasa de descuento de mercado (k), esta sería igual al dividendo dividido por el precio.

b) La empresa crece a un ritmo g durante infinito años.
c) La empresa no se endeuda para financiar el crecimiento.
d) La tasa de de crecimiento de los dividendos (g) siempre es menor a la tasa de descuento del mercado (k).

Problemas con el modelo

a) El modelo requiere una tasa de crecimiento de los dividendos (g), y esta tiene que ser menor a la tasa de descuento del mercado (k) y mayor a (-1).
b) Si la tasa de crecimiento de los dividendos (g) es muy cercana a la tasa de descuento del mercado (k) el modelo será muy volátil y el precio será muy alto.
c) Debido a su simplicidad, este modelo no considera variables importantes que afectan al valor futuro de la corriente de dividendos.
d) Hay empresas muy rentables que pagan dividendos muy pequeños o simplemente no los pagan.

El Modelo de Gordon-Shapiro

Uno de los modelos más conocidos de valoración del precio intrínseco de las acciones es el modelo de Gordon-Shapiro. Este modelo nos permite estimar el valor teórico de una acción en función del valor actual de sus dividendos futuros.

Para poder entender plenamente este post puede ser conveniente haber leído previamente los siguientes artículos:

• El valor temporal del dinero.
• ¿Qué nos indica la β de una acción?
• Cómo calcular la β con una hoja de cálculo.
• El modelo CAPM.
Los accionistas de una empresa suelen obtener rentabilidad de la misma a través de la captación de dividendos y de una posible ganancia de capital en la posterior venta de las acciones. Supongamos que una acción reparte un dividendo anual de 1€ y cotiza a 12€. Supongamos también que las previsiones apuntan a que este dividendo se va a incrementar a un ritmo constante de un 5% anual. En esta situación es lógico pensar que, puesto que las acciones cotizan a 12€ cuando reparte un dividendo de 1€, una vez que pase un año y la rentabilidad por dividendo se incremente en un 5% (manteniéndose estables las perspectivas de crecimiento futuras), la cotización de las acciones también debería de incrementarse en la misma proporción, llegando a cotizar a 12,60€.
Por lo tanto, calculando la TIR podemos afirmar que la rentabilidad bruta que nos ofrece esta inversión a un año es:

La rentabilidad anual de la inversión a dos años es:

Si suponemos que todas las variables permanecen constantes a lo largo del tiempo y realizamos las mismas operaciones para obtener la rentabilidad anual a 20 años vista, obtendremos los siguientes resultados:

Como podéis ver, no importa el plazo al que deseemos mantener nuestra inversión, la rentabilidad anual siempre será la misma: 13,75%. Esta rentabilidad no es casual, sino que está directamente relacionada con el riesgo sistemático de las acciones. Por otro lado, la tasa de crecimiento tampoco es casual, ya que está relacionada con otras variables como son: la rentabilidad exigida a las acciones, la rentabilidad sobre recursos propios (ROE) y la Tasa de Reparto de Dividendos (TRD). Y aquí es donde se encuentra el quid de la cuestión, ¿qué ocurriría si pudiésemos conocer de antemano cual es la tasa de rentabilidad y de crecimiento de la inversión? Pues que podríamos prever el valor teórico de la acción.

Lo que hace el modelo de de Gordon-Shapiro, básicamente es darle la vuelta a la función para que, conociendo únicamente el dividendo del año próximo, así como la rentabilidad y el crecimiento esperados, podamos determinar el valor teórico de la acción.

Conceptualmente hablando, lo que propone el modelo de descuento de dividendos es lo siguiente:

Matemáticamente lo expresaríamos de la siguiente manera:
Descuento de dividendos

• Pn: es el valor teórico de una acción para el año n.
• Dn: es el dividendo del año n, que se multiplica por (1+g) para obtener el dividendo del año próximo. También podemos poner en el numerador directamente el dividendo estimado para el próximo año.
• g: es la tasa anual y acumulativa de crecimiento de los dividendos y de las acciones.
• ke: es la tasa de rentabilidad anual bruta de la inversión.

En el modelo básico de descuento de dividendos se aplican las siguientes simplificaciones:

• Los dividendos crecen hasta el infinito a una tasa (g) anual y acumulativa.
• El precio de la acción crecerá a la misma tasa (g) que los dividendos.
• El rendimiento sobre las ganancias de capital esperadas debe ser constante e igual a (g).
• El rendimiento esperado por los inversores (ke) será igual a la suma de los rendimientos sobre los dividendos y sobre las ganancias de capital.

Si aplicamos el modelo al ejemplo anterior, éste quedaría así…
ejemplo de valor teórico

…y de esta manera podemos obtener la cotización teórica de las acciones para cualquier año. Como podéis comprobar, los valores teóricos de las acciones coinciden con las cotizaciones estimadas para cada año en la tabla anterior. No obstante, para que la cotización derivada de la aplicación del modelo sea realista es necesario que seamos capaces de determinar de manera fiable cuál será la tasa de descuento (ke) y la tasa de crecimiento (g). Con ánimo de ayudaros lograr estos objetivos, yo os propongo proceder de la siguiente manera:
1) El primer paso se basará en obtener unos datos de control sobre los que podremos trabajar posteriormente. Por ejemplo, supongamos que deseamos estimar el valor teórico de las acciones de Iberdrola. Para empezar, necesitaremos obtener los siguientes datos:

A) La cotización actual de las acciones de la compañía: 4,78€.

B) La previsión del dividendo a repartir para el próximo año: 0,27€.

C) La rentabilidad teórica de las acciones sin contar los dividendos. En el modelo de Gordon-Shapiro la rentabilidad anual de las acciones coincide con la rentabilidad anual de los dividendos, que a su vez es igual a la tasa de crecimiento esperada (g). Si recordáis, en el post anterior ya calculamos la rentabilidad esperada o exigida para las acciones de Iberdrola (que fue del 6,12%) mediante la aplicación del modelo CAPM.

D) Utilizando los 3 datos anteriores ya podemos calcular el 4º, que es la rentabilidad esperada, y la calcularemos como la TIR de la inversión de la siguiente manera:

Ahora ya tenemos unos datos que nos servirán de base para empezar a sacar conclusiones mediante la implementación del modelo de descuento de dividendos.

2.1) El siguiente paso consistirá en replantearnos todas las variables que hemos utilizado para la elaboración de los datos de control, haciéndonos las siguientes preguntas:

A) ¿Es adecuado el nivel de dividendos que hemos estimado para el próximo año? Un ajuste al alza del dividendo provocará un incremento del valor teórico de la acción y viceversa.

B) ¿Será sostenible a largo plazo la tasa de crecimiento (g)? Una mejora en las perspectivas de crecimiento futuras provocará un incremento automático del valor teórico de la acción y viceversa.

C) ¿La tasa de rentabilidad esperada (ke) alcanza un nivel suficiente como para cubrir nuestras expectativas de revalorización? Un incremento de la rentabilidad esperada reducirá el valor teórico de las acciones y viceversa.

2.2) Para modificar las variables y ajustar el modelo lo máximo posible a la realidad, es importante tener en cuenta los siguientes puntos:

Siempre hay que prever que la empresa repartirá un nivel razonable de dividendos en el futuro. Es posible que una empresa no reparta dividendos durante algunos años debido a motivos coyunturales, no obstante, una empresa que no tiene perspectivas futuras de pagar dividendos nunca, sencillamente carece de valor para el accionista como empresa en funcionamiento y debería procederse a su disolución.

El modelo no tiene en cuenta una futura ampliación o reducción de capital que podría provocar un sensible cambio en el dividendo por acción y, por lo tanto, en el valor teórico de las acciones. Puede ser conveniente hacer algún ajuste para incluir tal posibilidad.

La tasa de crecimiento no podrá ser en ningún caso superior a la tasa de rentabilidad ya que, en caso contrario, el valor teórico de la acción sería negativo, lo cual en la práctica es imposible. Por ejemplo, si tenemos una tasa de crecimiento de un 5%, esto significa que tanto las acciones como los dividendos crecen todos los años a esa tasa. Por lo tanto, sin necesidad de contar con los dividendos el crecimiento anual de las acciones ya nos proporciona una rentabilidad anual de un 5%, de manera que la rentabilidad total de las acciones más la de los dividendos siempre será superior a un 5%.

Si hay una diferencia muy baja entre la tasa de rentabilidad y la de crecimiento, los resultados obtenidos no serán realistas. Por ejemplo, para una empresa que repartiese un dividendo de 1€ y tuviese tasas de rentabilidad y de crecimiento del 1% y del 0,99% respectivamente, la aplicación del modelo de descuento de dividendos nos daría como resultado un valor teórico por acción de ¡¡10.000€!! Lo cual no tiene ningún sentido. Este es uno de los motivos por los que es importante aplicar el modelo mediante ligeros ajustes sobre los datos de control.

La tasa de crecimiento no puede ser superior al crecimiento a largo plazo de la economía (crecimiento del PIB nominal) o economías en las que la empresa realice sus actividades, ni superior al crecimiento a largo plazo del índice o índices en los que coticen las acciones. De no ser así llegaríamos al absurdo de que, en el infinito, la empresa tendería a representar prácticamente el 100% de la economía o del índice o índices en los que cotizase.

La tasa de crecimiento no debe ser inferior al resultado de multiplicar la Tasa de Retención de Beneficios (1 – Pay Out) por la Rentabilidad Sobre Recursos Propios (ROE). En caso contrario, estaríamos asumiendo que la empresa va a estar mal gestionada en el largo plazo.

Debido a la crisis económica que se ha venido desarrollando a lo largo de los últimos años, las empresas han visto como su ROE se reducía por debajo de la media histórica, por lo que han incrementado la Tasa de Reparto de Dividendos (Pay Out) hasta niveles muy superiores a los habituales con la intención de sostener la cotización de sus acciones. Por este motivo es conveniente calcular la tasa de crecimiento mínimo utilizando medias históricas, tanto de la Tasa de Retención de Beneficios como del ROE.

En lo que respecta a la Tasa de Rentabilidad (ke), ésta ha de compensar en todo momento el riesgo asumido en la compra de las acciones, ya que en caso contrario deberemos desechar inmediatamente tal inversión.

3) Seguimiento Posterior y Análisis de Escenarios:

Una vez que hemos ajustado el modelo para realizar una tasación relativamente fiable del valor teórico de las acciones, el siguiente paso sería realizar un seguimiento posterior de la modificación de las variables siempre intentando no desviarnos en exceso de la cotización actual. Esto último es especialmente relevante ya que en un mercado en el que se da competencia perfecta, debido a las características intrínsecas de este tipo de mercado, la cotización de las acciones no debería permanecer durante muchos años alejada de su valor teórico.

Por otro lado, el modelo de Gordon-Shapiro también nos puede servir para simular diferentes escenarios en los cuales se modifiquen las expectativas de dividendos, crecimiento o rentabilidad, con intención de prever cual sería su efecto sobre el valor teórico de las acciones en caso de producirse.

movimiento browniano es el movimiento aleatorio que se observa en algunas partículas microscópicas que se hallan en un medio fluido (por ejemplo, polen en una gota de agua). Recibe su nombre en honor al escocés Robert Brown, biólogo y botánico que descubrió este fenómeno en 1827 y observó que pequeñas partículas de polen se desplazaban en movimientos aleatorios sin razón aparente. En 1785, el mismo fenómeno había sido descrito por Jan Ingenhousz sobre partículas de carbón en alcohol.

El movimiento estocástico de estas partículas se debe a que su superficie es bombardeada incesantemente por las moléculas(átomos) del fluido sometidas a una agitación térmica.

Este bombardeo a escala atómica no es siempre completamente uniforme y sufre variaciones estadísticas importantes. Así, lapresión ejercida sobre los lados puede variar ligeramente con el tiempo, y así se genera el movimiento observado.

Tanto la difusión como la ósmosis se basan en el movimiento browniano.

La descripción matemática del fenómeno fue elaborada por Albert Einstein y constituye el primero de sus artículos del que, en la obra de Einstein, se considera el Annus Mirabilis ("año maravilloso", en latín), 1905. La teoría de Einstein demostraba la teoría atómica, todavía en disputa a principios del siglo XX, e iniciaba el campo de la física estadística.

Historia

El poema científico Sobre la Naturaleza de las cosas, del romano Lucrecio (60 a. C.), incluye la notable descripción de un movimiento browniano de partículas de polvo. El autor presentó este hecho como prueba de la existencia de los átomos:

Observa lo que acontece cuando rayos de sol son admitidos dentro de un edificio y cómo arroja la luz sobre los lugares oscuros. Puedes ver la multitud de pequeñas partículas moviéndose en un sinnúmero de caminos... su baile es un indicio de movimientos subyacentes de materia escondidos de nuestra vista... eso origina el movimiento de los átomos en sí mismos (p.e., espontáneamente). Entonces los pequeños organismos que son eliminados del impulso de los átomos son puestos en marcha por golpes invisibles y a su vez en contra de unos diminutos cañones. Así, el movimiento de los átomos emerge gradualmente de un nivel del sentido, que estos cuerpos están en movimiento como vemos en el rayo de sol, movidos por soplos que parecen invisibles.

Sobre la naturaleza de las cosas, Lucrecio

Jan Ingenhousz describió el movimiento irregular de partículas de carbón pulverizadas en la superficie del alcohol en 1785. No obstante, el descubrimiento del movimiento browniano se atribuye tradicionalmente al botánico Robert Brown en 1827. Se cree que Brown estuvo estudiando al microscopio partículas de polen flotando en el agua. Dentro de las vacuolas de los granos de polen observó diminutas partículas con movimientos nerviosos. Al repetir el experimento con partículas de polvo, concluyó que el movimiento no se debía a que las partículas de polen estaban "vivas", aunque no explicó el origen del movimiento.

El primero en describir matemáticamente el movimiento browniano fue Thorvald N. Thiele en 1880, en un documento sobre el método de los mínimos cuadrados. Fue seguido independientemente por Louis Bachelier en 1900, en su tesis doctoral La teoría de la especulación, en la que se presenta un análisis estocástico de acción y opción de mercados. Sin embargo, fue el estudio independiente de Albert Einstein en su artículo de 1905 (Über die von der molekularischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen / Sobre el movimiento postulado por la teoría cinética molecular del calor de pequeñas partículas suspendidas en un líquido estacionario) en el que mostró la solución a los físicos, como una forma indirecta de confirmar la existencia de átomos y moléculas.

En esa época la naturaleza atómica de la materia aún era una idea controvertida. Einstein y Marian Smoluchowski dedujeron que, si la teoría cinética de los fluidos era correcta, entonces las moléculas de agua tendrían movimientos aleatorios. Por lo tanto, las partículas pequeñas podrían recibir un número aleatorio de impactos, de fuerza aleatoria y de direcciones aleatorias, en cortos períodos de tiempo. Este bombardeo aleatorio por las moléculas del fluido podría ser suficiente para que las partículas pequeñas se moviesen de la manera exacta que Brown había descrito. Theodor Svedberg hizo importantes demostraciones del movimiento browniano encoloides, así como Felix Ehrenhaft lo hizo con partículas de plata en la atmósfera terrestre. Jean Perrin también realizó experimentos para verificar los modelos matemáticos, y al publicar sus resultados finales se puso fin a dos mil años de disputa sobre la realidad de las moléculas y los átomos.

Metáfora intuitiva del movimiento browniano

Considere un gran balón de 10 metros de diámetro. Imagine este balón en un estadio de fútbol o cualquier otra área llena de gente. El balón es tan grande que permanece por encima de la muchedumbre. Las personas aciertan a golpear el balón en diferentes momentos y direcciones de manera completamente aleatoria. Por ello, el balón no sigue una trayectoria. Ahora, considere una fuerza ejercida durante un cierto tiempo; podemos imaginar 20 personas empujando para la derecha y 21 para la izquierda y que cada persona está ejerciendo cantidades de fuerza equivalentes. En este caso las fuerzas ejercidas por el lado izquierdo y por el lado derecho no están equilibradas, favoreciendo al lado izquierdo, por lo que el balón se moverá ligeramente hacia la izquierda. Esta desproporción siempre existe, y es lo que causa el movimiento aleatorio. Si observáramos la situación desde arriba, de modo que no pudiéramos ver a las personas, veríamos el gran balón como un objeto animado por movimientos erráticos.

Ahora volvamos a la partícula de polen de Brown nadando aleatoriamente en el agua. Una molécula de agua mide aproximadamente 1 nm, mientras una partícula de polen tiene aproximadamente 1 µm de diámetro, 1000 veces mayor que una de agua. Así pues, la partícula de polen puede ser considerada como un gran balón empujado constantemente por las moléculas de agua. El movimiento browniano de las partículas en un líquido se debe a las desproporcionalidades instantáneas en las fuerzas ejercidas por las pequeñas moléculas líquidas sobre la partícula.

Modelos matemáticos para la descripción del movimiento browniano

La exposición matemática de esta definición corresponde a la ecuación que gobierna la evolución temporal de la función probabilística de densidad asociada con laecuación de difusión de una partícula browniana, y en definitiva es una ecuación diferencial parcial.

La evolución temporal de la posición de una partícula browniana en sí misma puede ser descrita aproximadamente por una ecuación de Langevin, la cual involucra un campo de fuerzas aleatorias que representan el efecto de fluctuaciones termales de una solución de partículas brownianas. En grandes escalas de tiempo, el movimiento browniano matemático se describe perfectamente con la ecuación de Langevin. A tiempos cortos, los efectos de la inercia prevalecen en esta ecuación. Sin embargo, se considera a esta ecuación, de otra manera la ecuación se vuelve singular, así que se debe eliminar el término de la inercia de esta ecuación para tener una descripción exacta, pero el comportamiento singular de estas partículas no se describe del todo.

Otras maneras de conseguir su modelo matemático consideran un movimiento browniano

B = (B_t)_{t \in [0,\infty]}

como un proceso de Gauss central con una funcióncovariante

\mathrm{Cov}(B_t,B_s) = \mathop{\rm min}(t,s)

para toda

t,s \geq 0

. El resultado de un proceso estocástico se le atribuye a Norbert Wiener, quedó demostrado en la teoría de probabilidad, existente desde 1923, y se conoce con el nombre de proceso de Wiener. Muchos detalles importantes aparecen en sus publicaciones.

Hay muchas posibilidades de construir un movimiento browniano:

La construcción abstracta por medio de esquemas de Kolmogórov, donde el problema viene con el aumento (o camino creciente).
La construcción de Lèvy-Ciesielski: se induce este movimiento con ayuda de un sistema de Haar de $C([0,1])$ a una base de Schauder, y se construye como un proceso estocástico con curva creciente.
Sea 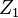$Z_0$ , $Z_1$ , … independiente, distribuida idénticamente y con distribución normal 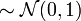$\sim \mathcal{N} (0, 1)$ . Luego:

S(t) = Z_0 t + \sum_{k=1}^\infty Z_k \frac{\sqrt{2} \sin(k \pi t)}{k \pi}

es un movimiento browniano.

Este fenómeno está muy relacionado también con la simulación de la cotización de las acciones.

La caracterización de Lévy del movimiento browniano

El matemático francés Paul Lévy propuso el siguiente teorema, donde la condición necesaria y suficiente para un Rⁿ continuo, evaluado en un proceso estocástico Xpara ser realmente n, dimensiona un movimiento browniano. Por lo tanto la condición de Lévy puede utilizarse realmente como una definición alternativa de movimiento browniano.

Entonces, X = (X₁, ..., X_n) sea un proceso estocástico continuo en un espacio probabilístico (Ω, Σ, P) tomando valores en Rⁿ. Tenemos la siguiente equivalencia:

X es un movimiento browniano con respecto a P, por ejemplo X con respecto a P es la misma que la n dimensional del movimiento browniano; por ejemplo, la medida de empuje X_∗(P) es una medida clásica de Wiener de C₀([0, +∞); Rⁿ).
tanto
1. X es una martingala con respecto a P como
2. para todo 1 ≤ i, j ≤ n, X_i(t)X_j(t) −δ_ijt es una martingala con respecto a P, donde δ_ij denota una delta de Kronecker.

Movimiento browniano en una variedad de Riemann

El generador infinitesimal (y, por lo tanto, el generador característico) de un movimiento browniano en Rⁿ puede calcularse fácilmente en ½Δ, donde Δ denota unoperador laplaciano. Esta observación es útil al definir un movimiento browniano en una variedad de Riemann m-dimensional (M, g): un movimiento browniano M se define como una difusión en M cuyo operador característico

\mathcal{A}

en coordenadas locales x_i, 1 ≤ i ≤ m, está dado por ½Δ_LB, donde Δ_LB es el operador de Laplace-Beltrami dado en las coordenadas por

$\Delta_{\mathrm{LB}} = \frac1{\sqrt{\det(g)}} \sum_{i = 1}^{m} \frac{\partial}{\partial x_{i}} \left( \sqrt{\det(g)} \sum_{j = 1}^{m} g^{ij} \frac{\partial}{\partial x_{j}} \right),$

donde [g^ij] = [g_ij]⁻¹ en el sentido de una matriz cuadrada inversa.

El movimiento browniano en la literatura

El siguiente fragmento es del capítulo 34 de la novela Rayuela, de Julio Cortázar:

Maga, vamos componiendo una figura absurda, dibujamos con nuestros movimientos una figura idéntica a la que dibujan las moscas cuando vuelan en una pieza, de aquí para allá, bruscamente dan media vuelta, de allá para aquí, eso es lo que se llama movimiento brownoideo, ¿ahora entendés?, un ángulo recto, una línea que sube, de aquí para allá, del fondo al frente, hacia arriba, hacia abajo, espasmódicamente, frenando en seco y arrancando en el mismo instante en otra dirección, y todo eso va tejiendo un dibujo, una figura, algo inexistente como vos y como yo, como los dos puntos perdidos en París que van de aquí para allá, de allá para aquí, haciendo su dibujo, danzando para nadie, ni siquiera para ellos mismos, una interminable figura sin sentido.

Otra novela en la que aparece el movimiento browniano es "Un viaje alucinante" de Isaac Asimov, novela en la que un equipo de científicos son miniaturizados a escala bacteriana y son introducidos en el torrente sanguíneo de un paciente en un submarino, detallándose los encuentros con distintos elementos como células, bacterias o virus, peripecia en la que sufren los efectos de dicho movimiento.

AMIGOS PARA SIEMPRE

Páginas

miércoles, 28 de octubre de 2015

Finanzas