viernes, 23 de octubre de 2015

Magnitudes físicas


Aceleración

En física, la aceleración es una magnitud vectorial que nos indica la variación de velocidad por unidad de tiempo. En el contexto de lamecánica vectorial newtoniana se representa normalmente por \vec a \, o \mathbf a \, y su módulo por a \,. Sus dimensiones son \scriptstyle [ L \cdot T^{-2} ]. Su unidad en elSistema Internacional es m/s2.
En la mecánica newtoniana, para un cuerpo con masa constante, la aceleración del cuerpo es proporcional a la fuerza que actúa sobre él mismo (segunda ley de Newton):
\mathbf{F} = m \mathbf{a} \quad \to \quad \mathbf{a} = \cfrac{\mathbf{F}}{m}
donde F es la fuerza resultante que actúa sobre el cuerpo, m es la masa del cuerpo, y a es la aceleración. La relación anterior es válida en cualquier sistema de referencia inercial.

Introducción

De acuerdo con la mecánica newtoniana, una partícula no puede seguir una trayectoria curva a menos que sobre ella actúe una cierta aceleración como consecuencia de la acción de una fuerza, ya que si esta no existiese, su movimiento sería rectilíneo. Asimismo, una partícula en movimiento rectilíneo solo puede cambiar su velocidadbajo la acción de una aceleración en la misma dirección de su velocidad (dirigida en el mismo sentido si acelera; o en sentido contrario si desacelera).
Algunos ejemplos del concepto de aceleración serían:
  • La llamada aceleración de la gravedad en la Tierra es la aceleración que produce la fuerza gravitatoria terrestre; su valor en la superficie de la Tierra es, aproximadamente, de 9,8 m/s2. Esto quiere decir que si se dejara caer libremente un objeto, aumentaría su velocidad de caída a razón de 9,8 m/s por cada segundo(siempre que omitamos la resistencia aerodinámica del aire). El objeto caería, por tanto, cada vez más rápido, respondiendo dicha velocidad a la ecuación:
v=at=gt=9,8\,t
  • Una maniobra de frenada de un vehículo, que se correspondería con una aceleración de signo negativo, o desaceleración, al oponerse a la velocidad que ya tenía el vehículo. Si el vehículo adquiriese más velocidad, a dicho efecto se le llamaría aceleración y, en este caso, sería de signo positivo.

Aceleración media e instantánea

Definición de la aceleración de una partícula en un movimiento cualquiera. Obsérvese que la aceleración no es tangente a la trayectoria.
Cada instante, o sea en cada punto de la trayectoria, queda definido un vector velocidad que, en general, cambia tanto en módulo como en dirección al pasar de un punto a otro de la trayectoria. La dirección de la velocidad cambiará debido a que la velocidad es tangente a la trayectoria y esta, por lo general, no es rectilínea. En la Figura se representan los vectores velocidad correspondientes a los instantes t y t+Δt, cuando la partícula pasa por los puntos P y Q, respectivamente. El cambio vectorial en la velocidad de la partícula durante ese intervalo de tiempo está indicado por Δv, en el triángulo vectorial al pie de la figura. Se define la aceleración media de la partícula, en el intervalo de tiempo Δt, como el cociente:
\langle\mathbf a\rangle = \mathbf{\bar{a}}= \frac{\Delta \mathbf v}{\Delta t}
Que es un vector paralelo a Δv y dependerá de la duración del intervalo de tiempo Δt considerado. La aceleración instantánea se la define como el límite al que tiende el cociente incremental Δv/Δt cuando Δt→0; esto es la derivada del vector velocidad con respecto al tiempo:
\mathbf{a}= \lim_{\Delta t \to 0}\frac{\Delta \mathbf v}{\Delta t} = \frac{d \mathbf v}{dt}
Puesto que la velocidad instantánea v a su vez es la derivada del vector posición r respecto al tiempo, la aceleración es la derivada segunda de la posición con respecto del tiempo:
\mathbf{a} = \frac{d^2 \mathbf{r}}{dt^2}
De igual forma se puede definir la velocidad instantánea a partir de la aceleración como:
\mathbf v - \mathbf{v}_0= \int_{t_0}^t \left({\mathrm{d}\mathbf{v} \over \mathrm{d}t}\right)\,\mathrm{d}t
Se puede obtener la velocidad a partir de la aceleración mediante integración:
\mathbf{v}= \int_0^t \mathbf{a}\ \mathrm{d}t + \mathbf{v}_0

Medición de la aceleración

La medida de la aceleración puede hacerse con un sistema de adquisición de datos y un simple acelerómetro. Los acelerómetros electrónicos son fabricados para medir la aceleración en una, dos o tres direcciones. Cuentan con dos elementos conductivos, separados por un material que varia su conductividad en función de las medidas, que a su vez serán relativas a la aceleración del conjunto.

Unidades

Las unidades de la aceleración son:
1 m/s2
1 cm/s2 = 1 Gal

Componentes intrínsecas de la aceleración: aceleraciones tangencial y normal

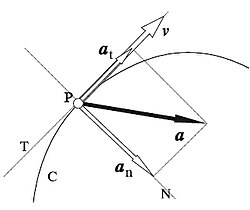
Componentes intrínsecas de la aceleración.
En tanto que el vector velocidad v es tangente a la trayectoria, el vector aceleración a puede descomponerse en dos componentes (llamadas componentes intrínsecas) mutuamente perpendiculares: una componente tangencial at (en la dirección de la tangente a la trayectoria), llamada aceleración tangencial, y una componente normal an (en la dirección de la normal principal a la trayectoria), llamada aceleración normal o centrípeta (este último nombre en razón a que siempre está dirigida hacia el centro de curvatura).
Derivando la velocidad con respecto al tiempo, teniendo en cuenta que el vector tangente cambia de dirección al pasar de un punto a otro de la trayectoria (esto significa que no es constante) obtenemos
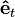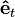\mathbf{a}= \frac{d\mathbf{v}}{dt} = \frac{d}{dt}(v \,\mathbf{\hat{e}}_t) = \frac{dv}{dt}\mathbf{\hat{e}}_t + v \frac{d\mathbf{\hat{e}}_t}{dt} = a_t \mathbf{\hat{e}}_t + v(\boldsymbol{\omega} \times \mathbf{\hat{e}}_{\text{t}})
siendo \mathbf{\hat{e}}_t el vector unitario tangente a la trayectoria en la misma dirección que la velocidad y \boldsymbol{\omega} la velocidad angular. Resulta conveniente escribir la expresión anterior en la forma
\mathbf{a}= \frac{d\mathbf{v}}{dt} = a_t \mathbf{\hat{e}}_t + \frac{v^2}{\rho} \mathbf{\hat{e}}_n = a_t \mathbf{\hat{e}}_t + a_n \mathbf{\hat{e}}_{\text{n}}
siendo
\mathbf{\hat{e}}_n el vector unitario normal a la trayectoria, esto es dirigido hacia el centro de curvatura de la misma,
\rho\, el radio de curvatura de la trayectoria, esto es el radio de la circunferencia osculatriz a la trayectoria.
Las magnitudes de estas dos componentes de la aceleración son:
a_t = \frac{dv}{dt} \qquad\qquad\qquad a_n=\frac{v^2}{\rho}
Cada una de estas dos componentes de la aceleración tiene un significado físico bien definido. Cuando una partícula se mueve, su velocidad puede cambiar y este cambio lo mide la aceleración tangencial. Pero si la trayectoria es curva también cambia la dirección de la velocidad y este cambio lo mide la aceleración normal.
  • Si en el movimiento curvilíneo la velocidad es constante (v=cte), la aceleración tangencial será nula, pero habrá una cierta aceleración normal, de modo que en un movimiento curvilíneo siempre habrá aceleración.
  • Si el movimiento es circular, entonces el radio de curvatura es el radio R de la circunferencia y la aceleración normal se escribe como an = v2/R.
  • Si la trayectoria es rectilínea, entonces el radio de curvatura es infinito (ρ→∞) de modo que an=0 (no hay cambio en la dirección de la velocidad) y la aceleración tangencial at será nula o no según que la velocidad sea o no constante.
Los vectores que aparecen en las expresiones anteriores son los vectores del triedro de Frênet que aparece en la geometría diferencial de curvas del siguiente modo:
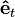\mathbf{\hat{e}}_t es el vector unitario tangente a la curva.
\mathbf{\hat{e}}_n es el vector unitario normal a la curva.
\boldsymbol{\omega} es el vector velocidad angular que es paralelo al vector binormal a la curva.

Movimiento circular uniforme

Cinemática del movimiento circular.
Un movimiento circular uniforme es aquel en el que la partícula recorre una trayectoria circular de radio R con velocidad constante, es decir, que la distancia recorrida en cada intervalo de tiempo igual es la misma. Para ese tipo de movimiento el vector de velocidad mantiene su módulo y va variando la dirección siguiendo una trayectoria circular. Si se aplican las fórmulas anteriores, se tiene que la aceleración tangencial es nula y la aceleración normal es constante: a esta aceleración normal se la llama "aceleración centrípeta". En este tipo de movimiento la aceleración se invierte en modificar la trayectoria del objeto y no en modificar su velocidad.
\mathbf{a}= \frac{d\mathbf{v}}{dt} = \frac{dv}{dt}\mathbf{\hat{e}}_t + \frac{v^2}{R} \mathbf{\hat{e}}_n = 0 \cdot \mathbf{\hat{e}}_t + \frac{v^2}{R} \hat{\mathbf{e}}_n = \omega^2 R \ \hat{\mathbf{e}}_n

Movimiento rectilíneo acelerado

En el Movimiento Rectilíneo Acelerado, la aceleración instantánea queda representada como la pendiente de la recta tangente a la curva que representa gráficamente la función v(t).
Si se aplican las fórmulas anteriores al movimiento rectilíneo, en el que solo existe aceleración tangencial, al estar todos los vectores contenidos en la trayectoria, podemos prescindir de la notación vectorial y escribir simplemente:
a= \frac{dv}{dt}
Ya que en ese tipo de movimiento los vectores \scriptstyle \mathbf{a} y \scriptstyle \mathbf{v} son paralelos, satisfaciendo también la relación:
v(t) = v_0 + \int_0^t a(\tau)\ d\tau
La coordenadas de posición viene dada en este caso por:
x(t) = x_0 + v_0t + \int_0^t (t-\tau)a(\tau)\ d\tau
Un caso particular de movimiento rectilíneo acelerado es el movimiento rectilíneo uniformemente variado donde la aceleración es además constante y por tanto la velocidad y la coordenadas de posición vienen dados por:
v(t) = v_0 + at, \qquad x(t) = x_0 + v_0 t + \frac{at^2}{2}

Aceleración en mecánica relativista

Relatividad especial

El análogo de la aceleración en mecánica relativista se llama cuadriaceleración y es un cuadrivector cuyas tres componentes espaciales para pequeñas velocidades coinciden con las de la aceleración newtoniana (la componente temporal para pequeñas velocidades resulta proporcional a la potencia de la fuerza dividida por la velocidad de la luz y la masa de la partícula).
En mecánica relativista la cuadrivelocidad y la cuadriaceleración son siempre ortogonales, eso se sigue de que la cuadrivelocidad tiene un (pseudo)módulo constante:
\mathbf{U}\cdot \mathbf{U} = c^2\ \Rightarrow\ 2\mathbf{U}\cdot \frac{d \mathbf{U}}{d\tau} = 0\ \Rightarrow\ 2\mathbf{U}\cdot \mathbf{A} = 0
Donde c es la velocidad de la luz y el producto anterior es el producto asociado a la métrica de Minkowski:
V\cdot W := \eta(V,W) = \eta_{\mu\nu}V^\mu V^\nu

Relatividad general

En teoría general de la relatividad el caso de la aceleración es más complicado, ya que debido a que el propio espacio-tiempo es curvo (ver curvatura del espacio-tiempo), una partícula sobre la que no actúa ninguna fuerza puede seguir una trayectoria curva, de hecho la línea curva que sigue una partícula sobre la que no actúa ninguna fuerza exterior es una línea geodésica, de hecho en relatividad general la fuerza gravitatoria no se interpeta como una fuerza sino como un efecto de la curvatura del espacio-tiempo que hace que las partículas no trayectorias rectas sino líneas geodéscias. En este contexto la aceleración no geodésica de una partícula es un vector cuyas cuatro componentes se calulan como:
A^\alpha = \frac{dU^\alpha}{d\tau} + \sum_{\beta,\gamma} \Gamma^\alpha_{\beta\gamma}U^\beta U^\gamma
Aquí \scriptstyle \alpha = 0, 1, 2, 3 (componente temporal y tres componentes espaciales). Se aprecia que cuando los símbolos de Christoffel \Gamma^\alpha_{\beta\gamma} una partícula puede tener aceleración cero aunque su cuadrivelocidad no sea constante, eso sucede cuando la partícula sigue una línea geodésica de un espacio-tiempo de curvatura no nula.


El concepto aceleración, no tiene que ver con ir moviéndose rápido.  Es un concepto que en muchas ocasiones ha sido mal utilizado en la vida real, sin embargo, su significado en física es muy diferente.  Es muy común escuchar que se utiliza este concepto para indicar que un objeto se mueve a gran velocidad lo cual es incorrecto.  El concepto aceleración se refiere al cambio en la velocidad de un objeto. Siempre que un objeto cambia suvelocidad, en términos de su magnitud o dirección, decimos que está acelerando. 
La Enciclopedia Encarta 2008 explica que la aceleración, se conoce también como aceleración lineal, y es la variación de la velocidad de un objeto por unidad de tiempo.  La velocidad se define como vector, es decir, tiene módulo (magnitud), dirección y sentido. De ello se deduce que un objeto se acelera si cambia su celeridad (la magnitud de la velocidad), su dirección de movimiento, o ambas cosas. Si se suelta un objeto y se deja caer libremente, resulta acelerado hacia abajo. Si se ata un objeto a una cuerda y se le hace girar en círculo por encima de la cabeza con celeridad constante, el objeto también experimenta una aceleración uniforme; en este caso, la aceleración tiene la misma dirección que la cuerda y está dirigida hacia la mano de la persona.
La aceleración es la razón de cambio en la velocidad respecto al tiempo. Es decir, la aceleración se refiere a cuan rápido un objeto en movimiento cambia su velocidad. Por ejemplo, un objeto que parte de reposo y alcanza una velocidad de 20 km/h, ha acelerado.  Sin embargo, si a un objeto le toma cuatro segundos en alcanzar la velocidad de 20 km/h, tendrá mayor aceleración que otro objeto al que le tome seis segundos en alcanzar tal velocidad.

Definimos la aceleración como el cambio en la velocidad respecto al tiempo durante el cual ocurre el cambio. El cambio en la velocidad (ΔV) es igual a la diferencia entre la velocidad final (Vf)y la velocidad inicial (Vi). Esto es: 

Por lo tanto definimos la aceleración matemáticamente como:

De la ecuación surge la posibilidad de que la aceleración sea positiva o negativa. La aceleración resulta ser positiva si el objeto aumentara su velocidad. Cuando el objeto aumenta la velocidad, entonces la velocidad final sería mayor que la inicial por lo que al restarlas para determinar la diferencia, la misma sería positiva. Por el contrario, si el objeto disminuye lavelocidad, entonces la aceleración sería negativa. La velocidad final sería menor que la inicial y por tanto la diferencia entre ambas sería negativa. En ambos casos, si la velocidad aumenta o disminuye, decimos que el objeto está acelerado. Sin embargo es muy común utilizar la palabra desaceleración para referirnos a la aceleración negativa. 
0 - 60 in seven seconds flat. by Reynolds, DanEl signo de la aceleración indica la dirección de la misma. Una aceleración positiva indica que la aceleración es en dirección al movimiento del objeto. La aceleración negativa indica que la misma es en dirección opuesta al movimiento del objeto. En próximas lecciones profundizaremos más en este aspecto.
 
Si ocurriera que la velocidad final y la inicial son iguales, entonces la aceleración sería igual a cero. Para que la velocidad final y la inicial sean iguales, el objeto tendría que moverse con velocidad constante. Por lo tanto, los objetos que se mueven con velocidad constante tienen una aceleración igual a cero.
Ahora, imagina un auto que se mueve alrededor de una pista circular. Si el chófer mantiene el velocímetro, digamos que en 20 mph, el auto se estaría moviendo con rapidez constante; pero su velocidad no lo sería. Recuerda que aceleración se refiere a un cambio en la magnitud o en la dirección de la velocidad. Si el auto se mueve en una pista circular, la dirección de la velocidad cambia constantemente con la posición del auto en la pista. Por tal motivo, decimos que aunque la magnitud de la velocidad sea constante (la rapidez), la dirección de la velocidad no lo es. Por tanto, el auto estaría acelerando.
 
La unidad para medir la aceleración según el Sistema Internacional de Medidas es el metro por segundo cuadrado (m/s²). Recuerda que el cambio en la velocidad se mide en m/s y al dividir esta unidad por el tiempo en segundos resulta (m/s)/s o m/s². 
 
 
Cuando conocemos la aceleración de un objeto, y esta es uniforme, podemos determinar su velocidad al cabo de un intervalo de tiempo. Para ello, resolveremos la ecuación de la definición de aceleración para la velocidad final.

 Si
Esta ecuación puede ser escrita así también:



 
 
 
 
En la pasada lección discutimos que para un objeto que se mueve con velocidad constante (a = 0), la gráfica de posición versus tiempo resulta ser una línea recta, como lo muestra la figura de la derecha.  Observa el diagrama de puntos que aparece en la parte izquierda de la gráfica.  Se puede observar que la distancia entre ellos es muy similar.
 
 
 
 
 
 
 
 
 
 
 
Si por el contrario el objeto se mueve con aceleración uniforme distinta de cero, entonces la gráfica de posición versus tiempo resulta ser una parábola.Ese es el caso de la imagen de la derecha.  En esta puedes observar que la distancia entre los puntos va aumentando más cada vez y por lo que esa distancia no es uniforme.


En este caso, el objeto se aleja del origen aumentando la velocidad uniformemente. El aumento uniforme en la velocidad, hace que el objeto recorra mayor distancia por unidad de tiempo según se aleja. Por ello, la gráfica resulta ser una parabólica. Observa que el cambio en la posición al principio es pequeño y el mismo va aumentando según pasa el tiempo. 
 
Si determinamos la velocidad instantánea del objeto cada segundo, observaríamos un aumento proporcional en la misma. Por lo que la gráfica de velocidad versus tiempo sería una lineal con lapendiente igual a la aceleración.  Puedes repasar estos conceptos en la unidad de Análisis gráfico del movimiento.



La aceleración positiva
Un camión de bomberos aumenta su velocidad de 0 a 21 m/s hacia el Este, en 3.5 segundos. ¿Cuál es su aceleración?
Ellis Nadler cartoon 
Dado:
Velocidad inicial (Vi): 0 m/s
Velocidad final (Vf): 21 m/s, Este
Tiempo (t): 3.5 segundos
Desconocida: Aceleración a=?
Ecuación básica:

Solución:

Respuesta:  Para indicar la aceleración debes indicar también la dirección.  Como el objeto se mueve hacia el este la respuesta es:  6m/s² , Este
El resultado indica que por cada segundo que transcurre, la velocidad del auto aumenta por 6.0 m/s.

Ejemplo 2:  La aceleración negativa
Un automóvil reduce su velocidad de 21m/s, Este a 7 m/s, Este, en 3.5.0 segundos. ¿Cuál es su aceleración?
Dado:
Velocidad inicial (Vi): 21 m/s, Este
Velocidad final (Vf): 7 m/s, Este
Tiempo (t): 3.5 segundos
Desconocida: Aceleración=?
Ecuación básica:

Solución:

Debemos considerar la dirección por lo que la respuesta de la pregunta es:  -4m/s² , Este.  El resultado indica que por cada segundo que transcurre, la velocidad del auto disminuye por 4 m/s. Fíjate que el auto va hacia el este y al la aceleración ser negativa, implica que el auto desacelera. 

Ejemplo 3:  La velocidad final bajo aceleración uniforme

Usando la ecuación de aceleración para determinar velocidad final.

Una pelota rueda por una cuesta inclinada durante 5 segundos, a una aceleración de 8 m/s². Si la pelota tiene una velocidad inicial de 2.0 m/s cuando comienza su recorrido, ¿Cuál será su velocidad al final del recorrido?
Dado:
Velocidad inicial (Vi): 2 m/s, bajando
Aceleración (a): 8 m/s², bajando
Tiempo (t): 5 segundos
Desconocida: Velocidad final (Vf) = ?
Ecuación básica:
Despeja para la desconocida que es la velocidad final:



Solución:

El resultado indica que la velocidad ira aumentando hasta alcanzar una velocidad de 42 m/s, bajando llegados los cinco segundos en movimiento.

Publicado por en

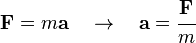
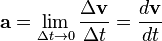
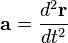
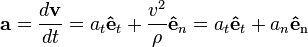
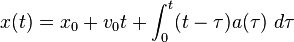
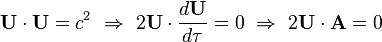
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)