viernes, 23 de octubre de 2015

Magnitudes físicas


aceleración angular como el cambio que experimenta la velocidad angular por unidad de tiempo. Se denota por la letra griega alfa \alpha. Al igual que la velocidad angular, la aceleración angular tiene carácter vectorial.
Se expresa en radianes por segundo al cuadrado, o s-2, ya que el radián es adimensional.

Definición matemática

Aceleración angular. En el caso general, cuando el eje de rotación no manteniene una dirección constante en el espacio, la aceleración angular no tiene la dirección del eje de rotación.
Definimos el vector aceleración angular, y lo representamos por \boldsymbol\alpha\,, de modo que
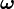\boldsymbol\alpha=\frac{d \boldsymbol\omega} {dt}
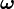siendo \boldsymbol\omega el vector velocidad angular del cuerpo alrededor del eje de rotación. Si denominamos por \mathbf e\, el vector unitario asociado a dicho eje, de modo que sea \boldsymbol\omega = \omega \mathbf e\,, podemos escribir
\boldsymbol\alpha= \frac{d \boldsymbol\omega} {dt} = \frac{d} {dt} \left(\omega\mathbf e\right)= \frac{d\omega}{dt}\mathbf e \ + \ \omega\frac{d\mathbf e}{dt}
resultando que, en general, el vector \boldsymbol\alpha\, no está localizado sobre el eje de rotación.
En el caso particular de que el eje de rotación mantenga una orientación fija en el espacio (movimiento plano), entonces será {d\mathbf e}/{dt}=0 y el vector aceleración angular \boldsymbol\alpha estará localizado sobre el eje de rotación. Esto es,
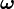\boldsymbol\alpha= \frac{d \boldsymbol\omega} {dt} = \frac{d\omega}{dt}\mathbf e = \alpha \,\,\mathbf e
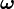de modo que el módulo de la aceleración angular, |\boldsymbol\alpha|=\alpha, es la derivada de la celeridad angular con respecto al tiempo (o la derivada segunda del ángulo de rotación con respecto al tiempo), su dirección es la de \boldsymbol\omega cuando la celeridad angular aumenta con el tiempo, o  -\boldsymbol\omega si disminuye.
En el caso general, cuando el eje de rotación no mantiene una dirección fija en el espacio, será {d\mathbf e}/{dt}\neq 0, aunque |\mathbf e|=1, ya que el vector unitario del eje cambia de dirección en el transcurso del movimiento. Puesto que \mathbf e es un versor, su derivada será un vector perpendicular a \mathbf e, esto es, al eje instantáneo de rotación.
Así pues, en el caso más general, la aceleración angular \boldsymbol\alpha se expresará en la forma
\boldsymbol\alpha= \frac{d \boldsymbol\omega} {dt} = \frac{d\omega}{dt}\mathbf e \ + \ \boldsymbol\Omega \times \boldsymbol\omega
siendo \boldsymbol\Omega la velocidad angular asociada a la rotación del eje o precesión del eje de rotación (definido por \,\mathbf e) en el espacio.
En la expresión anterior observaremos que el vector aceleración angular tiene dos componentes: una componente longitudinal (i.e., en la dirección del eje de rotación) cuyo módulo es {d\omega}/{dt}\, y una componente transversal (i.e., perpendicular al eje de rotación) cuyo módulo es \boldsymbol\Omega \times \boldsymbol\omega\,.
Así pues, en general,
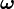  • el vector \boldsymbol\alpha no tendrá la misma dirección que el vector \boldsymbol\omega.
  • el vector aceleración angular \boldsymbol\alpha no tendrá la dirección del eje de rotación.
La dirección de la aceleración angular sólo coincide con la del vector velocidad angular, o sea, con el eje de rotación, en el caso de que dicho eje mantenga su orientación fija en el espacio, esto es, en el movimiento plano.

Movimiento plano

En el movimiento plano del sólido rígido, la aceleración angular, al igual que la velocidad angular, tiene la dirección del eje de rotación y viene dada por:
\alpha={d^2\theta\over dt^2}={d\omega\over dt}
donde \theta\, representa el ángulo girado en función de t y \omega la velocidad angular.
\omega={d\theta\over dt}
En el movimiento plano tanto la velocidad angular como la aceleración angular son vectores perpendiculares al plano en el que se produce el movimiento.

La aceleración angular (α) es la variación que experimenta la velocidad angular (ω) respecto al tiempo. La aceleración angular en el instante (t0) es:

Fórmula de la aceleración angular en el movimiento circular
La aceleración angular se expresa en radianes/segundo2 (rad/s2).

Aceleración angular en el movimiento circular uniforme (MCU)

En el movimiento circular uniforme (MCU) la aceleración angular es cero, ya que la velocidad angular es constante.

Aceleración angular en el movimiento circular uniformemente acelerado (MCUA)

La aceleración angular en el movimiento circular uniformemente acelerado es constante. Se representa como el incremento de velocidad angular ω desde el instante inicial hasta el final partido por el tiempo.

Fórmula de la aceleracion angular de una partícula en un movimiento circular uniformemente acelerado (MCUA)









La acutancia de una imagen es el grado de contraste que se observa en el límite entre detalles que difieren por su luminancia o densidad óptica. Cuanto más contrastado sea el límite entre una zona oscura y otra más clara, mayor es la acutancia y con ella la nitidez percibida en la imagen. La definición o resolución de la imagen no crecen cuando aumenta la acutancia, pero sí la capacidad para distinguir los detalles y la sensación subjetiva, que es la de un aumento de definición, de detalle. El sistema perceptivo visual humano es capaz de distinguir detalles más pequeños cuando su contraste es mayor.

Ampliación de la acutancia en una imagen digital. En la barra izquierda se ha acentuado exageradamente la acutancia; en el detalle (parte inferior) se ve que el efecto se debe a la amplificación del contraste entre píxeles contiguos.


El término "acutancia" designa el rendimiento óptico y la impresión de nitidez de la imagen. No existe una fórmula matemática para determinar la acutancia, sino que debe calcularse a simple vista (la acutancia es de carácter subjetivo). 
La impresión de la nitidez se caracteriza por la visibilidad de los detalles y micro-contrastes que componen una imagen. 
Asimismo, es necesario aclarar que no se debe confundir "un defecto de enfoque" con "acutancia" ya que se considera que la acutancia solo se puede apreciar cuando el enfoque es bueno. 
Para una mejor definición se puede decir que una mala acutancia a simple vista se compara a observar un sujeto a través de un cristal empañado, aunque en el exterior el sujeto sea nítido. 

Funcionamiento


La acutancia depende esencialmente de la calidad del objetivo. Las lentes, su tratamiento y el ensamblaje óptico juegan un papel importante en el grado de acutancia obtenido. 
Asimismo, la acutancia también depende de la apertura de diafragma y la distancia focal utilizada.
  • Con una apertura de diafragma máxima, la acutancia es menor que cuando el fotógrafo cierra el diafragma. Se considera que una buena acutancia se logra con una apertura entre f/8 y f/11. Sin embargo, este rango puede varia rsegún el tipo de objetivo.
  • Con un objetivo gran angular se logra una acutancia menor en los bordes en comparación con la que se logra en el centro. Este defecto varía según se utilice una distancia focal fija o un zoom. Asimismo, también puede variar según el fabricante.

Regulación de la acutancia

  • Durante la toma: si usted tiene una apertura plena de diafragma, deberá cerrarlo ya que una buena acutancia comienza entre un f/5.6 y un f/8.
  • Edición posterior: los programas de retoque permiten simular una mejor acutancia. Por lo general, este opción de simulación es llamada "nitidez" y permite mejorar la calidad de la imagen. Es necesario manejar esta opción con cuidado ya que si se utiliza demasiado puede alterar el redimiento óptico de la imagen (contornos aumentados, saturación, brillo...).

Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)