ángulo es la parte del plano comprendida entre dos semirrectas que tienen el mismo punto de origen o vértice.1 Suelen medirse en unidades tales como el radián, el grado sexagesimal o el grado centesimal.
Pueden estar definidos sobre superficies planas (trigonometría plana) o curvas (trigonometría esférica). Se denomina ángulo diedro al espacio comprendido entre dos semiplanos cuyo origen común es una recta. Un ángulo sólido es el que abarca un objeto visto desde un punto dado, midiendo su tamaño aparente.
Definición y características
Existen básicamente dos formas de definir un ángulo en el plano:
- Forma geométrica: Se le llama "ángulo" a la amplitud entre dos líneas de cualquier tipo que concurren en un punto común llamado vértice. Coloquialmente, ángulo es la figura formada por dos líneas con origen común. El ángulo entre dos curvas es el ángulo que forman sus rectas tangentes en el punto de intersección.
- Forma trigonométrica: Es la amplitud de rotación o giro que describe un segmento rectilíneo en torno de uno de sus extremos tomado como vértice desde una posición inicial hasta una posición final. Si la rotación es en sentido levógiro (contrario a las manecillas del reloj), el ángulo se considera positivo. Si la rotación es en sentido dextrógiro (conforme a las manecillas del reloj), el ángulo se considera negativo.
Definiciones clásicas
Euclides define un ángulo como la inclinación mutua de dos líneas que se encuentran una a otra en un plano y no están en línea recta. Según Proclo, un ángulo debe ser una calidad o una cantidad, o una relación. El primer concepto fue utilizado por Eudemo de Rodas, que describió un ángulo como desviación de una línea recta; el segundo por Carpo de Antioquía, que lo vio como el intervalo o el espacio entre las líneas que se intersecaban; Euclides adoptó un tercer concepto, aunque sus definiciones de ángulos rectos, agudos, y obtusos son cuantitativas.
Región angular
Se denomina región angular cada una de las dos partes en que queda dividido el plano por un ángulo.2
Amplitud de un ángulo
Se llama amplitud de un ángulo a la medida de este.2
Unidades de amplitud
Las unidades utilizadas para la medida de los ángulos del plano son:
- Radián (usado oficialmente en el Sistema Internacional de Unidades)
Los ángulos se pueden medir mediante utensilios tales como el goniómetro, el cuadrante, el sextante, la ballestina, el transportador de ángulos o semicírculo graduado, etc.
Tipos de ángulos
Los ángulos, de acuerdo con su amplitud, reciben estas denominaciones:
| Tipo | Descripción |
|---|---|
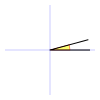
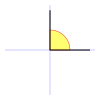
| Ángulo nulo | Es el ángulo formado por dos semirrectas coincidentes, por lo tanto su abertura es nula, o sea de 0°. |
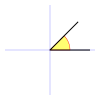
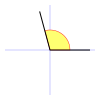
| Ángulo agudo | Es el ángulo formado por dos semirrectas con amplitud mayor de 0 rad y menor de  rad. rad.
Es decir, mayor de 0° y menor de 90° (grados sexagesimales), o menor de 100g (grados centesimales).
|
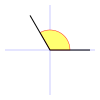
| Ángulo recto | Un ángulo recto es de amplitud igual a  rad. rad.
Es equivalente a 90° sexagesimales (o 100g centesimales).
Los dos lados de un ángulo recto son perpendiculares entre sí.
La proyección ortogonal de uno sobre otro es un punto, que coincide con el vértice. |
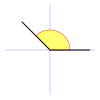
| Ángulo obtuso | Un ángulo obtuso es aquel cuya amplitud es mayor a  rad y menor a rad y menor a  rad. rad.
Mayor a 90° y menor a 180° sexagesimales (o más de 100g y menos de 200g centesimales).
|
| Ángulo llano | El ángulo llano tiene una amplitud de  rad. rad.
Equivalente a 180° sexagesimales (o 200g centesimales).
|
| Ángulo cóncavo | Ángulo que no es recto ni múltiplo de un ángulo recto.
Los ángulos agudos y obtusos son ángulos oblicuos.
|
| Ángulo completo o perigonal | Un ángulo completo o perigonal, tiene una amplitud de  rad. rad.
Equivalente a 360° sexagesimales (o 400g centesimales).
|
Ángulos convexo y cóncavo
En un plano, dos semirrectas (no coincidentes ni alineadas) con un origen común determinan siempre dos ángulos, uno convexo (el de menor amplitud) y otro cóncavo (el de mayor amplitud):1
| Tipo | Descripción |
|---|---|
| Ángulo convexo o saliente | Es el que mide menos de  rad. rad.
Equivale a más de 0° y menos de 180°sexagesimales (o más de 0g y menos de 200g centesimales).
|
| Ángulo cóncavo, reflejo o entrante | Es el que mide más de  rad y menos de rad y menos de  rad. rad.
Esto es, más de 180° y menos de 360° sexagesimales (o más de 200g y menos de 400g centesimales).
|
Ángulos relacionados
En función de su posición, se denominan:
- Ángulos adyacentes, los que tienen un vértice y un lado común, y semirrectas opuestas, pero no tienen ningún punto interior común, y suman 180°.
- Ángulos consecutivos, los que tienen un lado y el vértice común.
- Ángulos opuestos por el vértice, aquellos cuyos lados son semirrectas opuestas.
En función de su amplitud, se denominan:
- Ángulos congruentes, aquellos que tienen la misma amplitud, es decir, que miden lo mismo.
- Ángulos complementarios, aquellos cuya suma de medidas es π/2 radianes o 90°.
- Ángulos suplementarios, aquellos cuya suma de medidas es π radianes o 180°.
- Ángulos conjugados, aquellos cuyas medidas suman 2π radianes o 360°.
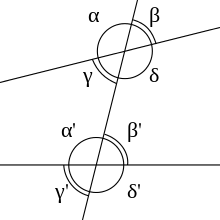
Cuando dos rectas son cortadas por una tercera en distindo punto:3
- Ángulos alternos: ángulos dispuestos a distinto lado de una recta que corta otras dos pero que no comparten lado.
-
 o
o  es alterno a
es alterno a  o a
o a 
-
 o
o  es alterno a
es alterno a  o a
o a 
- y viceversa.
- Ángulo alternos internos: ángulos comprendidos entre dos rectas pero situados a distinto lado de la recta cortante.
-
 es alterno interno a
es alterno interno a 
-
 es alterno interno a
es alterno interno a 
- Ángulo alternos externos: ángulos no comprendidos entre dos rectas pero situados a distinto lado de la recta que corta.
-
 es alterno externo a
es alterno externo a 
-
 es alterno externo a
es alterno externo a 
- Ángulos correspondientes, formados por dos paralelas y una transversal. Se encuentran en el mismo semiplano con respecto a la transversal y uno pertenece a la región interior y otro a la región exterior. Son congruentes.
Ángulos de un polígono
En función de su posición, se denominan:
- ángulo interior o interno de un polígono, es el formado por lados adyacentes, interiormente.
- ángulo exterior o externo de un polígono, es el conformado por un lado y la prolongación del adyacente.
Ángulos respecto de una circunferencia
Un ángulo, respecto de una circunferencia, pueden ser:
Ángulo central, si tiene su vértice en el centro de esta.
- La amplitud de un ángulo central es igual a la del arco que abarca.
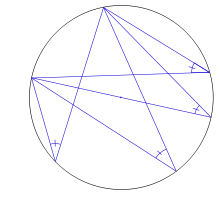
Ángulo inscrito, si su vértice es un punto de la circunferencia y sus lados la cortan en dos puntos.
- La amplitud de un ángulo inscrito es la mitad de la del arco que abarca. (Véase: arco capaz.)
Ángulo semi-inscrito, si su vértice está sobre esta, uno de sus lados la corta y el otro es tangente, siendo el punto de tangencia el propio vértice.
- La amplitud de un ángulo semi-inscrito es la mitad de la del arco que abarca.
Ángulo interior, si su vértice está en el interior de la circunferencia.
- La amplitud de un ángulo interior es la mitad de la suma de dos medidas: la del arco que abarcan sus lados más la del arco que abarcan sus prolongaciones;
Ángulo exterior, si tiene su vértice en el exterior de esta.
- La amplitud de un ángulo, no es la mitad de la diferencia de los dos arcos que abarcan sus lados sobre dicha circunferencia.
Trisección del ángulo
La trisección del ángulo es un problema clásico que consiste en dividir un ángulo dado en tres partes iguales usando solo regla y compás. En general, es imposible de resolver con esas condiciones.
Ángulos tridimensionales
- El ángulo diedro, es cada una de las dos partes del espacio delimitadas por dos semiplanos que parten de una recta común,
- El ángulo sólido, es la zona del espacio delimitada por una superficie cónica.
Coordenadas angulares tridimensionales
- Los ángulos de Euler, son tres coordenadas angulares que indican la orientación de un sistema de referencia de ejes ortogonales, normalmente móvil, respecto a otro fijo.
Ángulos en un espacio vectorial
Dado un espacio vectorial, cuyo cuerpo es el conjunto de los números reales y en el que existe un producto escalar entre vectores  , se define el ángulo formado por dos vectores no nulos
, se define el ángulo formado por dos vectores no nulos  e
e  mediante la expresión:
mediante la expresión:

Si el cociente anterior es 0, se dice que ambos vectores son ortogonales o perpendiculares. El cociente anterior está en el intervalo debido a la Desigualdad de Cauchy-Schwarz, lo que garantiza que siempre puede aplicarse el arcocoseno. Normalmente, se toma la rama del arcocoseno de forma que el ángulo que forman dos vectores siempre está en el intervalo
debido a la Desigualdad de Cauchy-Schwarz, lo que garantiza que siempre puede aplicarse el arcocoseno. Normalmente, se toma la rama del arcocoseno de forma que el ángulo que forman dos vectores siempre está en el intervalo ![[0,\pi]](https://upload.wikimedia.org/math/e/1/8/e1868564b62b4e2f1c063321df289469.png) (geométricamente, se elige el menor de los ángulos que forman dos vectores). Las principales propiedades que cumple el ángulo de dos vectores son las siguientes:
(geométricamente, se elige el menor de los ángulos que forman dos vectores). Las principales propiedades que cumple el ángulo de dos vectores son las siguientes:
 , se define el ángulo formado por dos vectores no nulos
, se define el ángulo formado por dos vectores no nulos  e
e  mediante la expresión:
mediante la expresión:
Si el cociente anterior es 0, se dice que ambos vectores son ortogonales o perpendiculares. El cociente anterior está en el intervalo
 debido a la Desigualdad de Cauchy-Schwarz, lo que garantiza que siempre puede aplicarse el arcocoseno. Normalmente, se toma la rama del arcocoseno de forma que el ángulo que forman dos vectores siempre está en el intervalo
debido a la Desigualdad de Cauchy-Schwarz, lo que garantiza que siempre puede aplicarse el arcocoseno. Normalmente, se toma la rama del arcocoseno de forma que el ángulo que forman dos vectores siempre está en el intervalo ![[0,\pi]](https://upload.wikimedia.org/math/e/1/8/e1868564b62b4e2f1c063321df289469.png) (geométricamente, se elige el menor de los ángulos que forman dos vectores). Las principales propiedades que cumple el ángulo de dos vectores son las siguientes:
(geométricamente, se elige el menor de los ángulos que forman dos vectores). Las principales propiedades que cumple el ángulo de dos vectores son las siguientes:- Si multiplicamos uno de los vectores por un escalar positivo, el ángulo no cambia.
- Si multiplicamos uno de los vectores por un escalar negativo, el ángulo pasa a ser el complementario.
- Se cumple el Teorema del coseno, es decir, dados
 e
e  no nulos,
no nulos,
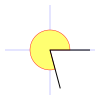
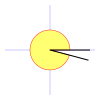
Galería de ángulos
 |  |  |  |  |  |
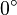 | 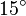 | 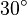 | 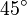 | 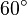 | 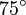 |
 |  |  |  |  |  |
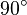 | 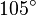 | 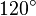 |  | 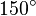 | 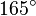 |
 |  | 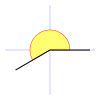 |  |  |  |
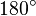 | 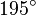 | 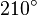 | 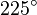 | 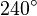 | 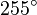 |
 |  |  |  |  |  |
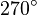 | 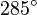 |  |  |  | 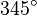 |
 | |||||
ángulo sólido es el ángulo espacial que abarca un objeto visto desde un punto dado, que se corresponde con la zona del espacio limitada por una superficie cónica. Mide el tamaño aparente de ese objeto.
La unidad del ángulo sólido en el SI es el estereorradián, cuyo símbolo es sr. Es el área del casquete esférico, en una esfera de radio unidad, abarcado por un cono cuyo vértice está en el centro de la esfera. Es una magnitud adimensional que se representa con la letra griega Ω.
Para calcular el ángulo sólido bajo el cual se ve un objeto desde un punto, se proyecta el objeto sobre una esfera de radio
 conocido, centrada en el punto de vista. Si la superficie de la proyección del objeto sobre la esfera es conocido, centrada en el punto de vista. Si la superficie de la proyección del objeto sobre la esfera es  , el ángulo sólido bajo el cual se ve el objeto es, por definición: , el ángulo sólido bajo el cual se ve el objeto es, por definición:Expresiones diferencial e integral
Consideremos una superficie dS (como se muestra en la figura) y unamos todos los puntos de su contorno con un punto O. De este modo obtendremos una superficie cónica, de vértice en O, que delimitará un área
 sobre la superficie de una esfera de radio unidad y centrada en O. Dicha área constituye la medida de ángulo sólido bajo el cual se ve la superficie dSdesde el punto O. sobre la superficie de una esfera de radio unidad y centrada en O. Dicha área constituye la medida de ángulo sólido bajo el cual se ve la superficie dSdesde el punto O.
La unidad de ángulo sólido es el estereorradián (sr), definido como el ángulo sólido que teniendo su vértice en el centro de una esfera, delimita un área en la superficie de la misma igual a la de un cuadrado cuyos lados sean iguales a la longitud del radio.
Por convenio, se dice que el ángulo sólido es positivo si desde el punto O se divisa la cara negativa (cóncava) de la superficie. El ángulo sólido será negativo si desde O se divisa la cara positiva (convexa) de la superficie. De acuerdo con las definiciones anteriores, es fácil comprender que el ángulo sólido bajo el cual se ve una superficie cerrada desde un punto O situado en el interior de la misma vale
 sr. Esto es así porque toda la superficie de la esfera de radio unidad, cuya área es sr. Esto es así porque toda la superficie de la esfera de radio unidad, cuya área es , quedará recubierta al proyectar sobre ella la superficie cerrada que la envuelve. , quedará recubierta al proyectar sobre ella la superficie cerrada que la envuelve.
En cambio, el ángulo sólido bajo el cual se ve una superficie cerrada desde un punto O exterior a la misma es nulo. Esto es así porque desde O vemos la cara positiva (convexa) de la superficie cerrada bajo un ángulo sólido que designaremos por
 . Inmediatamente detrás vemos la cara negativa (cóncava) de la superficie, bajo el mismo ángulo sólido, en valor absoluto, que designaremos por . Inmediatamente detrás vemos la cara negativa (cóncava) de la superficie, bajo el mismo ángulo sólido, en valor absoluto, que designaremos por  . Obviamente, resulta que . Obviamente, resulta que  . .
Busquemos ahora la expresión del elemento de ángulo sólido
 bajo el cual se ve un elemento de superficie dS desde un punto O, como se ilustra en la figura. El producto escalar bajo el cual se ve un elemento de superficie dS desde un punto O, como se ilustra en la figura. El producto escalar  representa la proyección del vector dS en la dirección radial er procedente de O y que pasa por el "centro" del elemento de superficie. Dicho de otro modo, representa la proyección del vector dS en la dirección radial er procedente de O y que pasa por el "centro" del elemento de superficie. Dicho de otro modo,  es la proyección del elemento de área dS sobre un plano perpendicular a la dirección de er. Ahora, una simple relación de semejanza entre la componente del área a una distancia es la proyección del elemento de área dS sobre un plano perpendicular a la dirección de er. Ahora, una simple relación de semejanza entre la componente del área a una distancia  y el área subtendida en la esfera unitaria (reconociendo que la superficie de una esfera varía como y el área subtendida en la esfera unitaria (reconociendo que la superficie de una esfera varía como  ), nos permite escribir: ), nos permite escribir:
que constituye la expresión matemática del ángulo sólido elemental. Entonces, el ángulo sólido bajo el cual se ve una superficie finita S desde un punto O será
Ejemplos
El ángulo sólido bajo el cual se ve un objeto depende tanto de las dimensiones del objeto como de la distancia a la que se encuentra del observador. Así, el ángulo sólido bajo el cual se ve una moneda de un céntimo de un euro a 1,80 m, la Luna o el Sol, es muy parecido (
 sr) a pesar de la enorme diferencia de dimensiones. sr) a pesar de la enorme diferencia de dimensiones.
Una hoja de papel normalizado A4 (210 mm x 297 mm), vista desde un punto centrado situado a 216 mm de la hoja se ve bajo un ángulo sólido de 1 sr, aproximadamente.
El ángulo sólido bajo el cual se ve un casquete esférico cuyo radio se ve bajo un ángulo
 desde el centro de la esfera, es desde el centro de la esfera, es
Desde un diedro rectángulo se ve bajo un ángulo sólido de
 sr (una esquina interior de una habitación). sr (una esquina interior de una habitación).
Desde un ángulo triedro rectángular se ve bajo un ángulo sólido de
 sr (una habitación vista del vértice del ángulo triedro formado por una esquina y el techo). sr (una habitación vista del vértice del ángulo triedro formado por una esquina y el techo).
La bóveda celeste abarca medio universo, es decir, un ángulo sólido
Desde cualquier punto en el espacio, el universo abarca un ángulo sólido de  sr. sr. sr. sr. |

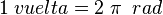
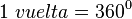
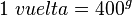











 .
.
No hay comentarios:
Publicar un comentario