El albedo es el porcentaje de radiación que cualquier superficie refleja respecto a la radiación que incide sobre la misma. Las superficies claras tienen valores de albedo superiores a las oscuras, y las brillantes más que las mates. El albedo medio de la Tierra es del 37-39% de la radiación que proviene del Sol.
Es una medida de la tendencia de una superficie a reflejar radiaciónincidente.
Un albedo alto enfría el planeta, porque la luz (radiación) absorbida y aprovechada para calentarlo es mínima. Por el contrario, un albedo bajo calienta el planeta, porque la mayor parte de la luz es absorbida por el mismo.
La presencia de agua en la Tierra crea una interesante realimentación positiva para el albedo, ya que las bajas temperaturas incrementan la cantidad de hielo sobre su superficie, lo que hace más blanco al planeta y aumenta su albedo, lo que a su vez enfría más el planeta, lo que crea nuevas cantidades de hielo; de esta manera, teóricamente al menos, podría llegarse al punto en que la Tierra entera se convertiría en una bola de nieve.
En astronomía ofrece un medio indirecto de averiguar la naturaleza de un astro mediante la comparación de su albedo con el de materias conocidas. El más alto registrado hasta el momento en el sistema solarcorresponde al del satélite Encélado de Saturno, y el más bajo, al de algunos asteroides carbonáceos, así como a los satélites marcianos Fobos y Deimos.
Variación del albedo
Las variaciones del albedo global son un hecho natural producido continuamente a lo largo de la historia geológica, debido a variaciones de origen exogénico y endogénico (deriva continental y los cambios en la distribución de mares y continentes).
A estas variaciones se superponen los intensos cambios ambientales potenciados por la actividad del hombre (utilización de combustibles fósiles para el tránsito vehicular, la actividad industrial y el uso doméstico).
Estas actividades provocan un aumento peligroso de los gases de invernadero, por consiguiente una disminución del albedo y un calentamiento global.
Una caída tan pequeña como de un 0,01 en el albedo de la tierra tendría una influencia en el clima mayor que el efecto de doblar la cantidad de dióxido de carbono en la atmósfera.
Física nuclear
En física nuclear, el albedo es la capacidad, por parte de una sustancia, de reflejar neutrones. Se mide por el cociente entre el número de neutrones reflejados y el número total de neutrones incidentes.
| Albedos | % de luz reflejada |
| Nieve reciente | 86 |
| Nubes brillantes | 78 |
| Nubes (promedio) | 50 |
| Desiertos terrestres | 21 |
| Suelo terrestre sin vegetación | 18 |
| Bosques (promedio) | 8 |
| Ceniza volcánica | 7 |
| Océanos | 5 a 10 |
| Sistema Solar (albedo medio) | |
|---|---|
| Luna | 7 |
| Mercurio | 6 |
| Venus (atmósfera) | 70 |
| Tierra vista desde el espacio | 37 a 39 |
| Marte | 15 |
| Júpiter | 41 |
| Saturno | 42 |
| Urano | 45 |
| Neptuno | 55 |
| Sistema Solar otros | |
| Encélado | 99 (el mayor registrado) |
| Meteoroides | 7 |
| Fobos | 6 |
| Deimos | 6 |
| Cometa Halley | 4 |
| Extrasolares | |
| TrES-2b | 0,04 (el menor registrado) |
Albedo
1) El albedo es la reflectividad de la superficie terrestre y se refiere a la energía reflejada desde la Tierra al universo. La radiación total (= radiación global) que llega a la superficie terrestre se compone de la suma de la radiación solar (la más importante) y la radiación difusa del universo. Al borde externo de la atmósfera terrestre llega una radiación que equivale a 1,35 KW por m2 . Es la constante solar. Sólo algo más de un 60 % de esta energía llega hasta el nivel del mar en las latitudes medias.
Un aumento de los gases de invernadero (del CO2, por ejemplo) disminuye el albedo, lo mismo que el enriquecimiento de la atmósfera en polvo atmosférico debido a erupciones volcánicas. En ambos casos se interpone materia adicional entre la superficie del planeta y el universo, disminuyendo así el retorno de energía al universo.
Imaginemos el supuesto caso de una nevada temprana de otoño sobre una de las grandes masas continentales del hemisferio norte y que cubra gran parte de los Estados Unidos y Canadá un manto blanco de nieve de altísima reflectividad. Tal cubierta de nieve podría aumentar de manera significativa el albedo global, si por alguna razón no llegara a fundirse hasta el comienzo del invierno y se quedara intacta hasta iniciada la primavera.En tal caso el balance térmico del planeta, podría verse alterado significativamente y el clima podría "saltar" de un estado de equilibrio a otro, o sea, se podría producir un cambio climático hacia condiciones más frías, debido a un albedo excesivo sobre un área de extensión continental
2) Desde un punto de vista más general, el albedo es "la relación de la luz reflejada desde unapartícula, un planeta o un satélite, con la luz incidente. Por eso, el valor (del albedo) es siempre menor a uno o igual a uno" (Porteous, 1992)
Alternativas:
Las variaciones del albedo global, son un hecho natural producido continuamente a lo largo de la historia geológica, debido a variaciones de origen exogénico y endogénico (deriva continental y los cambios en la distribución de mares y continentes).
A estas variaciones se superponen los intensos cambios ambientales potenciados por la actividad del hombre (utilización de combustibles fósiles para el tránsito vehicular, la actividad industrial y el uso doméstico).
Estas actividades provocan un aumento peligroso de los gases de invernadero, por consiguiente una disminución del albedo y un calentamiento global.
Estas actividades provocan un aumento peligroso de los gases de invernadero, por consiguiente una disminución del albedo y un calentamiento global.
Una solución parcial a este problema es el uso de energías alternativas no convencionales: energía solar, eólica, hidroeléctrica.

análisis dimensional es una herramienta que permite simplificar el estudio de cualquier fenómeno en el que estén involucradas muchas magnitudes físicas en forma de variables independientes. Su resultado fundamental, el teorema π de Vaschy-Buckingham (más conocido por teorema π) permite cambiar el conjunto original de parámetros de entrada dimensionales de un problema físico por otro conjunto de parámetros de entrada adimensionales más reducido. Estos parámetros adimensionales se obtienen mediante combinaciones adecuadas de los parámetros dimensionales y no son únicos, aunque sí lo es el número mínimo necesario para estudiar cadasistema. De este modo, al obtener uno de estos conjuntos de tamaño mínimo se consigue:
- Analizar con mayor facilidad el sistema objeto de estudio
- Reducir drásticamente el número de ensayos que debe realizarse para averiguar el comportamiento o respuesta del sistema.
El análisis dimensional es la base de los ensayos con maquetas a escala reducida utilizados en muchas ramas de la ingeniería, tales como la aeronáutica, la automoción o la ingeniería civil. A partir de dichos ensayos se obtiene información sobre lo que ocurre en el fenómeno a escala real cuando existe semejanza física entre el fenómeno real y el ensayo, gracias a que los resultados obtenidos en una maqueta a escala son válidos para el modelo a tamaño real si los números adimensionales que se toman como variables independientes para la experimentación tienen el mismo valor en la maqueta y en el modelo real. Así, para este tipo de cálculos, se utilizan ecuaciones dimensionales, que son expresiones algebraicas que tienen como variables a las unidades fundamentales y derivadas, las cuales se usan para demostrar fórmulas, equivalencias o para dar unidades a una respuesta.
Finalmente, el análisis dimensional también es una herramienta útil para detectar errores en los cálculos científicos e ingenieriles. Con este fin se comprueba la congruencia de las unidades empleadas en los cálculos, prestando especial atención a las unidades de los resultados.
Análisis dimensional
Para reducir un problema dimensional a otro adimensional con menos parámetros, se siguen los siguientes pasos generales:
- Contar el número de variables dimensionales n.
- Contar el número de unidades básicas (longitud, tiempo, masa, temperatura, etc.) m
- Determinar el número de grupos adimensionales. El número de grupos o números adimensionales (
 )es n - m.
)es n - m. - Hacer que cada número
 dependa de n - m variables fijas y que cada uno dependa además de una de las n - m variables restantes (se recomienda que las variables fijas sean una del fluido o medio, una geométrica y otra cinemática; ello para asegurar que los números adimensionales hallados tengan en cuenta todos los datos del problema).
dependa de n - m variables fijas y que cada uno dependa además de una de las n - m variables restantes (se recomienda que las variables fijas sean una del fluido o medio, una geométrica y otra cinemática; ello para asegurar que los números adimensionales hallados tengan en cuenta todos los datos del problema). - Cada
 se pone como un producto de las variables que lo determinan elevadas cada una a una potencia desconocida. Para garantizar adimensionalidad deben hallarse todos los valores de los exponentes tal que se cancelen todas las dimensiones implicadas.
se pone como un producto de las variables que lo determinan elevadas cada una a una potencia desconocida. Para garantizar adimensionalidad deben hallarse todos los valores de los exponentes tal que se cancelen todas las dimensiones implicadas. - El número
 que contenga la variable que se desea determinar se pone como función de los demás números adimensionales.
que contenga la variable que se desea determinar se pone como función de los demás números adimensionales. - En caso de trabajar con un modelo a escala, éste debe tener todos sus números adimensionales iguales a las del prototipo para asegurar similitud.
Aplicaciones del Análisis dimensional
- Detección de errores de cálculo.
- Resolución de problemas cuya solución directa conlleva dificultades matemáticas insalvables.
- Creación y estudio de modelos reducidos.
- Consideraciones sobre la influencia de posibles cambios en los modelos, etc.
Un ejemplo de Análisis dimensional
Calculemos mediante Análisis Dimensional la velocidad de un cuerpo en caída libre. Sabemos que dicha velocidad  dependerá de la altura
dependerá de la altura  y de la gravedad
y de la gravedad  . Pero imaginemos que también se nos ocurre decir que la velocidad depende de la masa
. Pero imaginemos que también se nos ocurre decir que la velocidad depende de la masa  . Una de las bondades del Análisis Dimensional es que es "autocorregible", es decir, el procedimiento, por sí sólo, elimina las unidades que no son necesarias.
. Una de las bondades del Análisis Dimensional es que es "autocorregible", es decir, el procedimiento, por sí sólo, elimina las unidades que no son necesarias.
 dependerá de la altura
dependerá de la altura  y de la gravedad
y de la gravedad  . Pero imaginemos que también se nos ocurre decir que la velocidad depende de la masa
. Pero imaginemos que también se nos ocurre decir que la velocidad depende de la masa  . Una de las bondades del Análisis Dimensional es que es "autocorregible", es decir, el procedimiento, por sí sólo, elimina las unidades que no son necesarias.
. Una de las bondades del Análisis Dimensional es que es "autocorregible", es decir, el procedimiento, por sí sólo, elimina las unidades que no son necesarias.- Identificar las magnitudes de las variables:
- Formar la matriz
- Hacer el producto de matrices:
Aquí tenemos que decir que  se refiere al exponente de la unidad
se refiere al exponente de la unidad  , pero eso se verá en pasos sucesivos.
, pero eso se verá en pasos sucesivos.
 se refiere al exponente de la unidad
se refiere al exponente de la unidad  , pero eso se verá en pasos sucesivos.
, pero eso se verá en pasos sucesivos.- Desarrollar el producto de matrices y resolver el sistema de ecuaciones.
Se forma un sistema de ecuaciones. Si nos fijamos, tenemos 4 incógnitas, y sólo 3 ecuaciones, así que para que el sistema pueda ser resuelto, necesitamos tantas incógnitas como ecuaciones. ¿Cómo se subsana el problema? Muy sencillo: se coge un  cualquiera y le asignamos el valor que queramos, a excepción del 0. En nuestro caso, vamos a tomar
cualquiera y le asignamos el valor que queramos, a excepción del 0. En nuestro caso, vamos a tomar  como
como  .
.
 cualquiera y le asignamos el valor que queramos, a excepción del 0. En nuestro caso, vamos a tomar
cualquiera y le asignamos el valor que queramos, a excepción del 0. En nuestro caso, vamos a tomar  como
como  .
.
Si aplicamos la solución inicial que hemos propuesto anteriormente ( ), se realizan los sencillos cálculos y llegamos a las soluciones:
), se realizan los sencillos cálculos y llegamos a las soluciones:
 ), se realizan los sencillos cálculos y llegamos a las soluciones:
), se realizan los sencillos cálculos y llegamos a las soluciones:- Formar el/los grupos
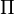
Un grupo 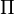 es una ecuación adimensional. ¿Cuántos grupos
es una ecuación adimensional. ¿Cuántos grupos 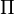 vamos a obtener? Pues si
vamos a obtener? Pues si  es el número de unidades (las unidades son el metro, el kilo, el segundo, el grado, ...), y
es el número de unidades (las unidades son el metro, el kilo, el segundo, el grado, ...), y  el rango máximo de la matriz que contiene los coeficientes de las magnitudes de las unidades (a veces coincide el rango de la matriz con el número de variables que tenemos, aunque ésta no es una regla fiable), el número de grupos
el rango máximo de la matriz que contiene los coeficientes de las magnitudes de las unidades (a veces coincide el rango de la matriz con el número de variables que tenemos, aunque ésta no es una regla fiable), el número de grupos 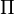 (o ecuaciones que obtendremos) será
(o ecuaciones que obtendremos) será 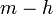 . En el caso que nos ocupa,
. En el caso que nos ocupa,  ecuación.
ecuación.
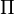 es una ecuación adimensional. ¿Cuántos grupos
es una ecuación adimensional. ¿Cuántos grupos 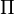 vamos a obtener? Pues si
vamos a obtener? Pues si  es el número de unidades (las unidades son el metro, el kilo, el segundo, el grado, ...), y
es el número de unidades (las unidades son el metro, el kilo, el segundo, el grado, ...), y  el rango máximo de la matriz que contiene los coeficientes de las magnitudes de las unidades (a veces coincide el rango de la matriz con el número de variables que tenemos, aunque ésta no es una regla fiable), el número de grupos
el rango máximo de la matriz que contiene los coeficientes de las magnitudes de las unidades (a veces coincide el rango de la matriz con el número de variables que tenemos, aunque ésta no es una regla fiable), el número de grupos 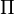 (o ecuaciones que obtendremos) será
(o ecuaciones que obtendremos) será 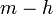 . En el caso que nos ocupa,
. En el caso que nos ocupa,  ecuación.
ecuación.
Ahora se cogen las unidades que hemos tomado en nuestro problema y las elevamos a los exponentes que hemos obtenido. Ésa es nuestra ecuación.
(Nótese que 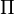 es adimensional). Aquí obtenemos aquello que llamábamos "autocorrección": el exponente de la masa es 0, así que desaparece de nuestra ecuación, demostrando una vez más que la caída libre no depende de la masa del objeto en cuestión.
es adimensional). Aquí obtenemos aquello que llamábamos "autocorrección": el exponente de la masa es 0, así que desaparece de nuestra ecuación, demostrando una vez más que la caída libre no depende de la masa del objeto en cuestión.
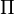 es adimensional). Aquí obtenemos aquello que llamábamos "autocorrección": el exponente de la masa es 0, así que desaparece de nuestra ecuación, demostrando una vez más que la caída libre no depende de la masa del objeto en cuestión.
es adimensional). Aquí obtenemos aquello que llamábamos "autocorrección": el exponente de la masa es 0, así que desaparece de nuestra ecuación, demostrando una vez más que la caída libre no depende de la masa del objeto en cuestión.- Paso final: obtención de la ecuación.
con  valiendo
valiendo  , lo que nos da la fórmula correcta:
, lo que nos da la fórmula correcta:
 valiendo
valiendo  , lo que nos da la fórmula correcta:
, lo que nos da la fórmula correcta:Principio de Fourier de homegeneidad dimensional
El principio de Fourier homogeneidad dimensional es un principio de buena formación de las expresiones que relacionan magnitudes físicas de manera algebraica. Es decir, es un principio de consistencia matemática que postula es posible sumar o restar entre sí magnitudes físicas de la misma naturaleza. En consecuencia, no podemos sumar longitud con tiempo, o masa con longitud, etc.
Ejemplo
El principio puede ilustrarse, con el ejemplo, de la energía de un cuerpo que es la suma de su energía cinética más su energía potencial:
Expresando la energía cinética y potencial tendremos:
Expresando la velocidad y la aceleración según las magnitudes fundamentales:
Expresado en forma dimensional:
Como puede verse tanto la energía cinética: un medio de la masa por la velocidad al cuadrado y la energía potencial: la masa por la gravedad y por la altura, es en ambos casos energía con la misma ecuación dimensional.
Por tanto, este principio de Fourier garantiza la coherencia de una ecuación física. Es importante recordar que si bien las constantes numéricas son adimensionales (ecuación dimensional igual a la unidad), por otro lado las constantes físicas tienen dimensión diferente de la unidad:
- e = 2,718281... (base de los logaritmos neperianos) →
![[e] = 1](https://upload.wikimedia.org/math/1/c/6/1c670a1ea6d7fb64d887568b72a1a99c.png) ;
; - c = 299 792 458 m/s (velocidad de la luz en el vacío) →
![[c] = [v] = LT^{-1}](https://upload.wikimedia.org/math/6/e/a/6ea89813a590867b9ee9a91e9c73ec9b.png)
Enunciado
A partir de las relaciones definitoriasVelocidad Cantidad de movimiento Aceleración Fuerza Trabajo Potencia Momento cinético Momento de una fuerza determine las ecuaciones dimensionales de estas magnitudes, así como sus unidades en el SI en función de las unidades básicas de este sistema.2 Velocidad
La velocidad se define como la derivada de la posición respecto al tiempo. Una derivada no es más que un cociente entre dos cantidades muy pequeñas y por tanto sus dimensiones serán las del numerador divididas por las del denominador, esto es,La unidad en el SI de velocidad es 1 m/s.3 Cantidad de movimiento
La cantidad de movimiento es el producto de la masa por la velocidad, por lo que sus dimensiones serán las del producto de estas dos cantidades:La unidad SI de la cantidad de movimiento es 1 kg·m/s.4 Aceleración
La aceleración es la derivada de la velocidad respecto al tiempo, por tantoLa unidad de aceleración en el SI será 1 m/s².5 Fuerza
La fuerza se define como la derivada de la cantidad de movimiento con respecto al tiempo (aunque también suele expresarse como el producto de la masa por la aceleración). Por elloLa unidad SI de la fuerza es el newton, que equivale a6 Trabajo
El trabajo se define a partir de una integral, esto es, una suma de muchas cantidades muy pequeñas. Las dimensiones de la integral son entonces las mismas que las de cada uno de los sumandos. Cada sumando es un trabajo diferencial, igual al producto escalar de una fuerza por un desplazamiento. Por elloVemos que el trabajo posee dimensiones de masa por velocidad al cuadrado, que son las mismas de la energía cinéticaLa unidad de trabajo en el sistema internacional es el julio, equivalente a7 Potencia
La potencia es el cociente entre un trabajo diferencial y el tiempo diferencial en que se realiza. Las dimensiones las da también el cocienteLa unidad SI de potencia es el vatio, que equivale a8 Momento cinético
El momento cinético es el producto vectorial de la posición por la cantidad de movimiento. Todo producto (de escalares, escalar, vectorial,…) tiene dimensiones del producto de las magnitudes, esto es,La unidad de momento cinético en el SI será 1 kg·m²/s.9 Momento de una fuerza
Por último, el momento de una fuerza equivale al producto vectorial de un vector de posición (con dimensiones de distancia) y una fuerzaLa unidad de momento en el SI es el newton por metroAunque esta unidad es equivalente a un julio, no se utiliza 1 J como unidad de momento de una fuerza, debido a que esta magnitud no representa trabajo, calor o energía, cantidades para las que se reserva el uso del julio.
![[v] =
m/s =
LT^{-1}](https://upload.wikimedia.org/math/0/c/9/0c9ab6c2d5098abbeeeb9999fab4d3fd.png)
![[g] =
m/s^2 =
LT^{-2}](https://upload.wikimedia.org/math/7/d/3/7d37df33c40f72460db095c9809b9bba.png)
![[h] =
m =
L](https://upload.wikimedia.org/math/4/e/0/4e0026a92f3e611ef27f817e236c7a54.png)
![[m] =
kg =
M](https://upload.wikimedia.org/math/1/c/3/1c3ccf37aa68529360e3a48dfa575e09.png)
![\begin{array}{cc}
&
\begin{bmatrix}
{[h]}&{[g]}&{[v]}&{[m]}
\end{bmatrix}
\\
\begin{bmatrix}
{\textbf{M}} \\
{\textbf{L}} \\
{\textbf{T}}
\end{bmatrix}
&
{\begin{bmatrix}
{0}&{0}&{0}&{1} \\
{1}&{1}&{1}&{0} \\
{0}&{-2}&{-1}&{0}
\end{bmatrix}}
\end{array}](https://upload.wikimedia.org/math/5/f/8/5f870ca0f0315ef44f457400ffd6b268.png)











![E =
\frac{1}{2} \, [M] [L]^2 [T]^{-2} +
[M] [L]^2 [T]^{-2}](https://upload.wikimedia.org/math/f/1/5/f155895d77a13a33a844023d2db03722.png)
No hay comentarios:
Publicar un comentario