viernes, 23 de octubre de 2015

Magnitudes físicas


La cantidad de movimiento, momento lineal, ímpetu o momentum es una magnitud física fundamental de tipo vectorial que describe el movimiento de un cuerpo en cualquier teoría mecánica. En mecánica clásica, la cantidad de movimiento se define como el producto de la masa del cuerpo y su velocidad en un instante determinado. Históricamente, el concepto se remonta aGalileo Galilei. En su obra Discursos y demostraciones matemáticas en torno a dos nuevas ciencias, usa el término italianoimpeto, mientras que Isaac Newton en Principia Mathematica usa el término latino motus1 (movimiento) y vis motrix (fuerza motriz). Momento y momentum son palabras directamente tomadas del latín mōmentum, término derivado del verbo mŏvēre'mover'.
La definición concreta de cantidad de movimiento difiere de una formulación mecánica a otra: en mecánica newtoniana se define para una partícula simplemente como el producto de su masa por la velocidad, en la mecánica lagrangiana o hamiltoniana se admiten formas más complicadas en sistemas de coordenadas no cartesianas, en la teoría de la relatividad la definición es más compleja aun cuando se usan sistemas inerciales, y en mecánica cuántica su definición requiere el uso de operadores autoadjuntos definidos sobre un espacio vectorial de dimensión infinita.
En mecánica newtoniana, la forma más usual de introducir la cantidad de movimiento es como el producto de la masa (kg) de un cuerpo material por su velocidad (m/s), para luego analizar su relación con las leyes de Newton. No obstante, tras el desarrollo de la física moderna, esta manera de operar no resultó ser la más conveniente para abordar esta magnitud fundamental. El defecto principal es que esta definición newtoniana esconde el concepto inherente a la magnitud, que resulta ser una propiedad de cualquier ente físico con o sin masa, necesaria para describir las interacciones. Los modelos actuales consideran que no sólo los cuerpos másicos poseen cantidad de movimiento, también resulta ser un atributo de los campos y los fotones.
La cantidad de movimiento obedece a una ley de conservación, lo cual significa que la cantidad de movimiento total de todosistema cerrado (o sea uno que no es afectado por fuerzas exteriores, y cuyas fuerzas internas no son disipadoras) no puede ser cambiada y permanece constante en el tiempo.
En el enfoque geométrico de la mecánica relativista la definición es algo diferente. Además, el concepto de momento lineal puede definirse para entidades físicas como los fotones o los campos electromagnéticos, que carecen de masa en reposo.

Cantidad de movimiento en mecánica clásica

Mecánica newtoniana

Históricamente el concepto de cantidad de movimiento surgió en el contexto de la mecánica newtoniana en estrecha relación con el concepto de velocidad y el de masa. En mecánica newtoniana se define la cantidad de movimiento lineal como el producto de la masa por la velocidad:
\mathbf{p} = m \mathbf{v}
La idea intuitiva tras esta definición está en que la "cantidad de movimiento" dependía tanto de la masa como de la velocidad: si se imagina una mosca y un camión, ambos moviéndose a 40 km/h, la experiencia cotidiana dice que la mosca es fácil de detener con la mano mientras que el camión no, aunque los dos vayan a la misma velocidad. Esta intuición llevó a definir una magnitud que fuera proporcional tanto a la masa del objeto móvil como a su velocidad.

Mecánica lagrangiana y hamiltoniana

En las formulaciones más abstractas de la mecánica clásica, como la mecánica lagrangiana y la mecánica hamiltoniana, además del momento lineal y del momento angular se pueden definir otros momentos, llamados momentos generalizados o momentos conjugados, asociados a cualquier tipo de coordenada generalizada. Se generaliza así la noción de momento.
Si se tiene un sistema mecánico definido por su lagrangiano L definido en términos de las coordenadas generalizadas (q1,q2,...,qN) y las velocidades generalizadas, entonces el momento conjugado de la coordenada qi viene dado por:2
p_i = \frac{\partial L}{\partial \dot{q}_i}
Cuando la coordenada qi es una de las coordenadas de un sistema de coordenadas cartesianas, el momento conjugado coincide con una de las componentes del momento lineal, y, cuando la coordenada generalizada representa una coordenada angular o la medida de un ángulo, el momento conjugado correspondiente resulta ser una de las componentes del momento angular.

Cantidad de movimiento de un medio continuo

Si estamos interesados en averiguar la cantidad de movimiento de, por ejemplo, un fluido que se mueve según un campo de velocidades es necesario sumar la cantidad de movimiento de cada partícula del fluido, es decir, de cada diferencial de masa o elemento infinitesimal:
\mathbf{p}=\int \mathbf{v}\ dm = \int_V \mathbf{v}\ \rho dV

Cantidad de movimiento en mecánica relativista

La constancia de la velocidad de la luz en todos los sistemas inerciales tiene como consecuencia que la fuerza aplicada y la aceleración adquirida por un cuerpo material no sean colineales en general, por lo cual la ley de Newton expresada como F=ma no es la más adecuada. La ley fundamental de la mecánica relativista aceptada esF=dp/dt.
El principio de relatividad establece que las leyes de la física conserven su forma en los sistemas inerciales (los fenómenos siguen las mismas leyes). Aplicando este principio en la ley F=dp/dt se obtiene el concepto de masa relativista, variable con la velocidad del cuerpo, si se mantiene la definición clásica (newtoniana) de la cantidad de movimiento.
En el enfoque geométrico de la mecánica relativista, puesto que el intervalo de tiempo efectivo percibido por una partícula que se mueve con respecto a un observadordifiere del tiempo medido por el observador. Eso hace que la derivada temporal del momento lineal respecto a la coordenada temporal del observador inercial y la fuerza medida por él no coincidan. Para que la fuerza sea la derivada temporal del momento es necesario emplear la derivada temporal respecto al tiempo propio de la partícula. Eso conduce a redefinir la cantidad de movimiento en términos de la masa y la velocidad medida por el observador con la corrección asociada a la dilatación de tiempo experimentada por la partícula. Así, la expresión relativista de la cantidad de movimiento de una partícula medida por un observador inercial viene dada por:3
\mathbf{p} = \frac{m\mathbf{v}}{ \sqrt{1-\cfrac{v^2}{c^2}} } = \gamma m\mathbf{v}
donde v^2, c^2 son respectivamente el módulo al cuadrado de la velocidad de la partícula y la velocidad de la luz al cuadrado y \gamma es el factor de Lorentz.
Además, en mecánica relativista, cuando se consideran diferentes observadores en diversos estados de movimiento surge el problema de relacionar los valores de las medidas realizadas por ambos. Eso sólo es posible si en lugar de considerar vectores tridimensionales se consideran cuadrivectores que incluyan coordenadas espaciales y temporales. Así, el momento lineal definido anteriormente junto con la energía constituye el cuadrivector momento-energía o cuadrimomento P:
\mathbf{P} = (P^0, P^1, P^2, P^3) = \left(\frac{E}{c},p_x, p_y, p_z\right)
Los cuadrimomentos definidos como en la última expresión medidos por dos observadores inerciales se relacionarán mediante las ecuaciones suministradas por lastransformaciones de Lorentz.

Cantidad de movimiento en mecánica cuántica

La mecánica cuántica postula que a cada magnitud física observable m\, le corresponde un operador lineal autoadjunto \hat{m}, llamado simplemente "observable", definido sobre un dominio de espacio de Hilbert abstracto. Este espacio de Hilbert representa cada uno de los posibles estados físicos que puede presentar un determinado sistema cuántico.
Aunque existen diversas maneras de construir un operador asociado a la cantidad de movimiento, la forma más frecuente es usar como espacio de Hilbert para una partícula el espacio de Hilbert L^2(\R^3) y usar una representación de los estados cuánticos como funciones de onda. En ese caso, las componentes cartesianas del momento lineal se definen como:
\hat{p}_x = -i\hbar\frac{\partial}{\partial x} \qquad \hat{p}_y = -i\hbar\frac{\partial}{\partial y} \qquad \hat{p}_z = -i\hbar\frac{\partial}{\partial z}
Resulta interesante advertir que dichos operadores son autoadjuntos sólo sobre el espacio de funciones absolutamente continuas de L^2(\R^3) que constituyen un dominio denso de dicho espacio. Cuidado con esto, pues los autovalores del operador momento, salvo que nos limitemos a L^2(\R^3), no tienen por qué ser reales. De hecho, en general pueden ser complejos.

Conservación

Mecánica newtoniana

En un sistema mecánico de partículas aislado (cerrado) en el cual las fuerzas externas son cero, el momento lineal total se conserva si las partículas materiales ejercen fuerzas paralelas a la recta que las une, ya que en ese caso dentro de la dinámica newtoniana del sistema de partículas puede probarse que existe una integral del movimiento dada por:
\mathbf{P}( \mathbf{r}_i , \dot{\mathbf{r}}_i ) = \sum_{i=1}^{N} m_i \dot{\mathbf{r}}_{i}
Donde \mathbf{r}_i,\dot{\mathbf{r}}_i son respectivamente los vectores de posición y las velocidades para la partícula i-ésima medidas por un observador inercial.

Mecánica lagrangiana y hamiltoniana

En mecánica lagrangiana «si el lagrangiano no depende explícitamente de alguna de las coordenadas generalizadas entonces existe un momento generalizado que se mantiene constante a lo largo del tiempo», resultando por tanto esa cantidad una integral del movimiento, es decir, existe una ley de conservación para dicha magnitud. Pongamos por caso que un sistema mecánico tiene un lagrangiano con n grados de libertad y su lagrangiano no depende de una de ellas. Por ejemplo, la primera de ellas, es decir:
L:U\subset \R^{2n} \to \R, \qquad (\mathbf{q},\dot{\mathbf{q}}) \mapsto L(\mathbf{q},\dot{\mathbf{q}}) = \sum_{i,j} \dot{q}_i\frac{g_{ij}(q_2,...,q_n)}{2}\dot{q}_j \ - \ V(q_2,...,q_n)
En ese caso, en virtud de las ecuaciones de Euler-Lagrange existe una magnitud conservada p_1\, que viene dada por:
0 = \frac{d}{dt}\left( \frac{\partial L}{\partial \dot{q}_1} \right) - \frac{\partial L}{\partial q_1} = \frac{d}{dt}\left(\sum_j g_{ij}\dot{q}_j\right) \ - \ 0 \Rightarrow p_1 = \frac{\partial L}{\partial \dot{q}_1} = \sum_j g_{ij}\dot{q}_j = \mbox{constante}
Si el conjunto de coordenadas generalizadas usado es cartesiano entonces el tensor métrico es la delta de Kronecker g_{ij}(q_2,...,q_n) = \delta_{ij} y la cantidad p_1\, coincide con el momento lineal en la dirección dada por la primera coordenada.
En mecánica hamiltoniana existe una forma muy sencilla para determinar si una función que depende de las coordenadas y momentos generalizados da lugar o no a una ley de conservación en términos del paréntesis de Poisson. Para determinar esa expresión calculemos la derivada a lo largo de la trayectoria de una magnitud:
\frac{df(\mathbf{p},\mathbf{q})}{dt} = \sum_i\left(\frac{\partial f}{\partial q_i}\dot{q}_i + \frac{\partial f}{\partial p_i}\dot{p}_i\right) = \sum_i\left(\frac{\partial f}{\partial q_i}\frac{\partial H}{\partial p_i} + \frac{\partial f}{\partial p_i}\frac{\partial H}{\partial q_i}\right) = \{f,H\}_{pq}
A partir de esa expresión podemos ver que para «un momento generalizado se conservará constante en el tiempo, si y sólo si, el hamiltoniano no depende explícitamente de la coordenada generalizada conjugada» como se puede ver:
0 = \frac{dp_j}{dt} = \{p_j,H\}_{pq} = \sum_i\left( 0 \cdot \frac{\partial H}{\partial p_i} + \delta_{ij}\frac{\partial H}{\partial q_i}\right) = \frac{\partial H}{\partial q_j}

Mecánica del medio continuo

Si estamos interesados en averiguar la cantidad de movimiento de, por ejemplo, un fluido que se mueve según un campo de velocidades es necesario sumar la cantidad de movimiento de cada partícula del fluido, es decir, de cada diferencial de masa o elemento infinitesimal:
\mathbf{p}=\int \mathbf{v}\ dm = \int_V \mathbf{v}\ \rho dV
Si se introduce el tensor de tensiones que caracteriza las fuerzas internas en el interior de un medio continuo la ecuación de balance de la cantidad de movimiento en términos de las fuerzas exteriores se puede expresar como:
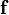\boldsymbol{\nabla\cdot\sigma} + \rho \mathbf{f} = \rho \frac{d\mathbf{v}}{dt}
donde:
\boldsymbol{\sigma} es el tensor de tensiones de Cauchy.
\rho\, es la densidad de materia.
\mathbf{f} la densidad de fuerza sobre el cuerpo.
\mathbf{v} la velocidad en cada punto del medio continuo.

Mecánica relativista

En teoría de la relatividad la cantidad de movimiento o cuadrimomento se define como un vector P el producto de la cuadrivelocidad U por la masa (en reposo) de una partícula:
P^\alpha = mU^\alpha\ = m\frac{dx^\alpha}{d\tau}
En relatividad general esta cantidad se conserva si sobre ella no actúan fuerzas exteriores. En relatividad general la situación es algo más compleja y se puede ver que la cantidad de movimiento se conserva para una partícula si esta se mueve a lo largo de una línea geodésica. Para ver esto basta comprobar que la derivada respecto altiempo propio se reduce a la ecuación de las geodésicas, y esta derivada se anula si y sólo si la partícula se mueve a lo largo de una línea de universo que sea geodésica:4
\frac{dP^\alpha}{d\tau} = U^\beta\nabla_\beta P^\alpha = U^\beta\left[m\frac{dU^\alpha}{dx^\beta}+ m\Gamma^\alpha_{\gamma\beta}U^\gamma \right] = m\left[ \frac{d^2x^\alpha}{d\tau^2}+ \Gamma^\alpha_{\gamma\beta} \frac{dx^\gamma}{d\tau} \frac{dx^\beta}{d\tau} \right]
En general para un cuerpo macroscópico sólido de cierto tamaño en un campo gravitatorio que presenta variaciones importantes de un punto a otro del cuerpo no es posible que cada una de las partículas siga una línea geodésica sin que el cuerpo se fragmente o perdiendo su integridad. Esto sucede por ejemplo en regiones delespacio-tiempo donde existen fuertes variaciones de curvatura. Por ejemplo en la caída dentro de un agujero negro, las fuerzas de marea resultantes de la diferente curvatura del espacio-tiempo de un punto a otro despedazarían un cuerpo sólido cayendo dentro de un agujero negro.

Mecánica cuántica

Como es sabido en mecánica cuántica una cantidad se conserva si el operador autoadjunto que representa a dicha magnitud u observable conmuta con el hamiltoniano, de modo similar a como en mecánica hamiltoniana una magnitud se conserva si el paréntesis de Poisson con el hamiltoniano se anula. Tomando como espacio de Hilbert del sistema de una partícula dentro de un potencial una representación de tipo L^2(\R^3). Se tiene que:
\frac{d \hat{p}_i}{d t} = -\frac{i}{\hbar}[\hat{p}_i, \hat{H}] = - \boldsymbol{\nabla} V(x_i)
Por tanto, si el potencial no depende de las coordenadas x_i , entonces la cantidad de movimiento de la partícula se conserva. Además, la última expresión es formalmente equivalente a la del caso clásico en términos del paréntesis de Poisson. Teniendo en cuenta claro está, que éste es el hamiltoniano cuántico, y que las cantidades físicas, no son las mismas que en la mecánica clásica, sino operadores que representan las cantidades clásicas (observables).

La cantidad de movimiento o momento lineal se refiere a objetos en movimientos y es una magnitud vectorial que desempeña un papel muy importante en la segunda ley de Newton. La cantidad de movimiento combina las ideas de inercia y movimiento. También obedece a un principio de conservación que se ha utilizado para descubrir muchos hechos relacionados con las partículas básicas del Universo. La ley de la conservación de la cantidad de movimiento y la ley de la conservación de la energía, son las herramientas más poderosas de la mecánica. La conservación de la cantidad de movimiento es la base sobre la que se construye la solución a diversos problemas que implican dos o más cuerpos que interactúan, especialmente en la comprensión del comportamiento del choque o colisión de objetos.
Introducción
 
La expresión “cantidad de movimiento” suena extraña porque hasta el mismo movimiento no existe hasta tanto no se vea el objeto moverse de un lugar a otro o rotar sobre un eje. Generalmente se asocia movimiento con velocidad . Otro parámetro asociado a la cantidad de movimiento es la masa . Esto significa que a mayor masa mayor cantidad de movimiento. De igual forma si se aumenta la velocidad también aumenta la cantidad de movimiento.

Cuando usted practica tenis y golpea la pelota contra una pared a cierta velocidad; La esférica rebota contra usted a una velocidad sólo un poco menor. Si juega golf, le pega a una pequeña pelota plástica con un palo pesado; inmediatamente después la pelota deja el “tee” a una gran velocidad viajando por el aire cientos de metros, una distancia mayor de la que se podría alcanzar arrojándola. Si se dispara un rifle, se retrocede contra el hombro cuando la bala viaja a lo largo del cañón y sale por la boca. ¿Qué particularidades en común tienen estos ejemplos?

En cada caso un objeto, la pelota de tenis, la pelota de golf o la bala, experimenta un cambio drástico en su velocidad y sufre una aceleración muy grande.
 
  1. El intervalo de tiempo durante el cual se lleva a cabo esta aceleración es relativamente corto. ¿Qué significa esto? La fuerza promedio que actúa sobre el objeto debe ser bastante grande.
     
  2. En cada caso un segundo objeto manifiesta un cambio mucho menor en su velocidad; según la tercera ley de Newton, el objeto debe haber experimentado una fuerza de reacción de igual magnitud, pero en dirección opuesta y el retroceso del rifle, el cambio de velocidad de la cabeza del palo de golf y la velocidad aparentemente cero de la pared.

Fuerzas externas e internas
Al analizar el comportamiento de un sistema de varios cuerpos, es conveniente distinguir entre fuerzas internas y externas. Las fuerzas internas son aquellas por las cuales todas las partes del sistema actúan entre sí. Las fuerzas externas son aquellas que influyen fuera del sistema sobre uno o más de los cuerpos de éste o sobre el sistema completo.

Una experiencia común indica que todo objeto en movimiento posee una cualidad que lo hace ejercer una fuerza sobre todo cuando se le intenta detener. Cuanta mayor sea la rapidez con que se desplaza, más difícil será detenerlo. Además, cuanta mayor masa tenga, más difícil será pararlo.

Newton le dio el nombre de movimiento a esta cualidad de un objeto en movimiento. Hoy se le llama cantidad de movimiento o momento lineal.
Y se define del modo siguiente.
Cantidad de movimiento = masa x velocidad
= m. 
Donde  es el símbolo con que se representa la cantidad de movimiento.
es un vector que apunta en la misma dirección que .
 
Unidades:
En el MKS: Kg.m/seg.
         CGS: gr.cm/seg.
La cantidad de movimiento es grande si el objeto tiene gran masa y velocidad.La cantidad de movimiento de un objeto de masa m y velocidad  es igual al producto de la masa y la velocidad.
 

También puede verse que un barco de grandes dimensiones que navegue a baja velocidad tiene una gran cantidad de movimiento, como lo tiene una bala pequeña disparada a alta velocidad. Y por supuesto, un objeto enorme que se desplace a alta velocidad.

Cuando una bala o un camión chocan contra una pared, se ejerce contra ésta una gran fuerza. ¿De donde proviene tal fuerza? De un cambio de velocidad. La fuerza de impacto es proporcional a la razón de cambio de velocidad del objeto en movimiento. Y a mayor masa de ese objeto, mayor fuerza; así, la fuerza de impacto es también proporcional a la masa del objeto en movimiento.

Variación en la cantidad de movimientoCuando ocurre un cambio en la masa y en la velocidad, en ambas a la vez, existirá un cambio en la cantidad de movimiento del cuerpo considerado.
Si la masa permanece constante pero la velocidad del cuerpo cambia de  a  se tendrá que.
 = m. en el primer instante
    = m. en el segundo instante
La variación de la cantidad de movimiento será:
 -  = m . - m. =>  - = m.(  -  ) luego  =m.
Estas ideas son congruentes con la segunda ley de Newton,
La segunda ley de Newton, en términos de la cantidad de movimiento, establece que la fuerza sobre un objeto es igual a la rapidez de cambio de la cantidad de movimiento del objeto. Es decir:

Una bala se acelera cuando se ejerce una fuerza sobre ella. Cuán rápido se mueva al final, no obstante, depende de algo además de su masa y la fuerza impartida. La velocidad final depende del tiempo. Una fuerza sostenida por un tiempo largo empuja la bala a una velocidad mayor que la misma fuerza aplicada brevemente.
Se puede expresar la segunda ley de Newton de otra forma, haciendo más evidente el factor tiempo, sustituyendo el término para la aceleración por su definición (el cambio en velocidad por tiempo).
Relaciones entre el impulso y la cantidad de movimiento.La segunda ley de Newton expresa que = m. ; Como  = ; se puede escribir
= m. ; Luego .  = m. para concluir que = . , es decir el cambio de la cantidad de movimiento es el producto de la fuerza (su promedio respecto al tiempo) y el intervalo de tiempo  a lo largo del cual actúa dicha fuerza).
El producto . ; Se denomina impulso .

 
El impulso es la magnitud medida por el producto de la fuerza aplicada a un cuerpo y el intervalo de tiempo durante el cual actúa.

Teorema del impulso y de cantidad de movimientoEl impulso resultante ejercido sobre una partícula durante cierto intervalo de tiempo es igual a la variación de la cantidad de movimiento de la partícula.
Si  es la fuerza que actúa y  = t1 - t2 el intervalo de tiempo, se puede escribir matemáticamente que; = . t. Luego = 

 
El impulso, para el cual no se utiliza ningún signo convencional, es una cantidad vectorial dirigida a lo largo de la fuerza media . Tiene las mismas unidades y dimensiones que la cantidad de movimiento, aunque se acostumbra, al tratar sobre impulso, usar la unidadNewton segundo (MKS) y Dina segundo(CGS).

 
Para modificar la cantidad de movimiento es necesario considerar el impulso, o sea la magnitud de la fuerza y el tiempo de contacto. Un golfista golpea una pelota con gran fuerza para impartirle momento; pero para obtener elmáximo momento, efectúa un movimiento complementario, prolongado el tiempo de contacto de la fuerza sobre la pelota. Una fuerza grande multiplicada por un tiempo grande da por resultado un gran impulso, el cual produce un mayor cambio en el momento de la pelota. Las fuerzas que intervienen en el impulso no son fuerzas de valores permanentes, sino que por lo general varían de un instante a otro.

Ahora considere el caso de un cuerpo que inicialmente tiene un momento hasta que se detiene por medio de un impulso. Un auto que se desplaza a alta velocidad, choca contra un muro de contención. El gran momento se “extingue” en un tiempo muy breve. Compárense los resultados para un auto a alta velocidad que choca contra un muro de concreto y contra un montón de heno. En ambos casos, el momento del auto es el mismo, por lo que el impulso necesario para detenerlo en cada caso es el mismo.

Sin embargo, los tiempos de impacto son diferentes. Cuando el auto golpea el muro de concreto, ese tiempo es corto, por lo que la fuerza promedio de impacto es enorme.
En cambio, cuando golpea el montón de heno, el impulso se prolonga por un tiempo mayor y la fuerza de impacto es considerablemente menor.

La noción de tiempo corto de contacto explica por qué una experta en Kárate puede romper una pila de ladrillos golpeando con su mano libre. Ella dirige su brazo y mano velozmente contra los ladrillos con considerable momento. Ese momento se reduce de forma drástica cuando aplica un impulso a los ladrillos. El impulso es la fuerza de la mano contra los ladrillos multiplicada por el tiempo que la mano hace contacto con ellos. Por medio de una rápida ejecución, la experta hace que el tiempo de contacto sea lo más corto posible y, en consecuencia, que la fuerza de impacto
sea enorme.

 
Ante un puñetazo con gran momento, un pugilista trata de reducir al mínimo la fuerza de impacto. Si no puede evitar el golpe, al menos tiene la alternativa de elegir las magnitudes relativas de  y tpara lograr el impulso que le permite absorber y cambiar el momento de puñetazo que proviene de su oponente. La fuerza de impacto se aminora si se prolonga este tiempo de impacto; en consecuencia, el pugilista “se va con el golpe” o “hace rolling”.

Una persona cae más suavemente sobre un piso de madera que sobre uno de concreto. ¿Por qué? Se debe a la “elasticidad”, porque permite un tiempo mayor de impacto y por tanto una fuerza menor de impacto.

Cantidad de movimiento de un sistema de PartículasLa cantidad total de movimiento del sistema de partículas es la suma vectorial de las cantidades vectoriales de las partículas individuales. Es decir:  =  +  +  + ... 
Para ello se representan las cantidades de movimiento en un sistema de ejes rectangulares y se descomponen en sus componentes.

Ejemplo de tres partícula
Componentes de : P1x = - P1.cosa
                               P1y =   P1.sena
Componentes de : P2x= P2.cosß
                               P2y= P2.senß
Componentes de : P3x= P3.cos Y
                               P3y= -P3.sen Y

 


Sumatoria de las componentes según el eje x :
Px = P1x + P2x + P3xSumatoria de las componentes según el eje y:
Py = P1y + P2y + P3yLos componentes Px y Pyse representa en un sistema ejes rectangulares y se determina el vector cantidad de movimiento cuyo módulo es:
El anterior procedimiento es válido para un número cualquiera de partículas.





Ejemplo de colisión elástica (m1 = 4 kg, u1 = 5 m/s, m2 = 4 kg, u2 = 0 m/s) de dos cuerpos de la misma masa: todo el momento lineal es transferido del primero al segundo.
Ejemplo de colisión elástica (m1 = 1000 kg, u1 = 5 m/s, m2 = 0,1 kg, u2 = 0 m/s) de un objeto muy pesado contra otro muy ligero, existe una pequeña transferencia de momento al más ligero que sale disparado a mayor velocidad, mientras que el primer cuerpo apenas sufre una ligera deceleración v1 = 4,999 m/s, v2 = 9,999 m/s
Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)