Teoría de cuerpos
criterio de Eisenstein proporciona una condición suficiente para que un polinomio sea irreducible sobre el conjunto de los números racionales.
y un número primo  tal que
tal que
 tal que
tal que divide a todo
divide a todo 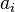 para i ≠ n
para i ≠ n no divide a
no divide a 
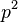 no divide a
no divide a 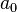
entonces  es irreducible sobre
es irreducible sobre ![\scriptstyle \mathbb{Q}[x]](https://upload.wikimedia.org/math/9/a/0/9a0e44f33b7891943944e2689f7bd78b.png) .
.
 es irreducible sobre
es irreducible sobre ![\scriptstyle \mathbb{Q}[x]](https://upload.wikimedia.org/math/9/a/0/9a0e44f33b7891943944e2689f7bd78b.png) .
.Ejemplos
Considérese  .
.
 .
.
Probaremos los siguientes primos  .
.
 .
.- p = 2
- 2 no divide a 15, entonces probaremos
- p = 3
- 3 no divide a 10, entonces probaremos
- p = 5
- 5 divide a 15, el coeficiente de x, y a 10, el término constante. Además, 5 no divide a 3, el primer coeficiente; y 25 = 52 no divide a 10. Concluiremos, por lo tanto, que g(x) es irreducible.
En algunos casos, la elección del primo puede ser poco clara, pero puede llegar a revelarse por un cambio de variable y = x + a. Por ejemplo, consideremos h(x) = x2 + x+ 2. Es aparentemente difícil, ya que ningún primo divide a 1, el coeficiente de x. Pero si cambiamos h(x) en h(x + 3) = x2 + 7x + 14 veremos inmediatamente que el primo 7 divide al coeficiente de x y al término constante, y que 49 no divide a 14. Así, con el cambio introducido, logramos que el polinomio satisficiera el criterio de Eisenstein.
Otro caso notable es el del polinomio ciclotómico para un primo p. Esto es:
(xp − 1)/(x − 1) = xp − 1 + xp − 2 + ... + x + 1.
Aquí, el polinomio satisface el criterio de Eisenstein, en una nueva variable y, después de establecer x = y + 1. El coeficiente constante será entonces p; los otros coeficientes son divisibles por p por las propiedades de los coeficientes binomiales C(p,k) que son p! dividido por algo que no involucra a p.
Prueba elemental
Considérese f(x) como un polinomio módulo p; esto es, redúzcanse los coeficientes al cuerpo Z/pZ. Entonces será c.xn para una constante c distinta de cero. Dado que dichos polinomios tienen una factorización única, cualquier factorización de f mod p resultará en monomios. Ahora, si f no fuese irreducible como polinomio entero, podríamos escribirlo como g.h, y f mod p como el producto de g mod p y h mod p. Estos últimos deben ser monomios, como acabamos de afirmar, por lo que tendremos que g mod p es d.xk y h mod p es e.xn-k donde c = d.e.
Vemos ahora que las condiciones dadas sobre g mod p y h mod p significan que p2 dividirá a a0, lo que contradice nuestra hipótesis. De hecho a0 será g(0).h(0) y pdivide a ambos factores, como hemos dicho más arriba.
Explicación avanzada
Aplicando la teoría del polígono de Newton para el campo de los números p-ádicos, para un polinomio de Eisenstein, se supone que tomaremos la menor envolturaconvexa de los puntos.
- (0,1), (1, v1), (2, v2), ..., (n − 1, vn-1), (n,0),
donde vi es la evaluación p-ádica de ai (es decir, la mayor potencia de p que lo divide). Ahora, los datos que tenemos sobre los vi for 0 < i < n, es decir, que existe por lo menos uno, es lo que necesitamos para concluir que la menor envoltura convexa es exactamente el único segmento de (0,1) a (n,0), con pendiente −1/n.
De la teoría general sabemos que p se ramifica completamente en la extensión de los números p-ádicos generados por una raíz de f. Por esa razón, f es irreducible sobre el campo p-ádico, y a fortiori sobre el campo de los números racionales.
Esta prueba es mucho más complicada que el argumento directo por reducción módulo p. Sin embargo, permite ver, en términos de teoría algebraica de números, la frecuencia con que puede aplicarse el criterio de Eisenstein después de algún cambio de variable; y así limita marcadamente la posible elección de p.
De hecho sólo los primos p que se ramifiquen en la extensión de Q generada por una raíz de f tienen alguna posibilidad de servir. Pueden ser hallados en términos deldiscriminante de f. Por ejemplo, en el caso de x2 + x + 2 dado más arriba, el discriminante es −7, de modo que 7 es el único primo con posibilidades de satisfacer el criterio. Se torna, mod 7, en:
- (x − 3)2
— es inevitable la repetición de una raíz, ya que el discriminante es 0 mod 7. Por lo tanto el cambio de variable es algo realmente predecible.
Una vez más, para el polinomio ciclotómico se torna en:
- (x − 1)p − 1 mod p;
Por métodos de álgebra lineal puede demostrarse que el discriminante es pp − 2 (excepto variación de signo).
De igual modo que cuando se trabaja con números enteros muchas veces es conveniente expresarlos como producto de números primos, cuando se trabaja con polinomios muchas veces es conveniente expresarlos como producto de polinomios irreducibles (véase la entrada de ayer para la definición de polinomio irreducible). Es decir, el papel que juegan los polinomios irreducibles dentro de los polinomios es similar al que juegan los números primos dentro de los numeros enteros.
Sin embargo, hay algunas diferencias. Dado un número natural, por muy grande que sea, se puede saber de forma “rápida” (en el futuro espero tratar de forma más precisa lo que quiero decir por rápida) si dicho número es primo o no. (En cualquier caso, hay un algoritmo claro para saber si es primo o no: dado  , basta con ver si algún número natural
, basta con ver si algún número natural  divide a
divide a  , y esto es un número finito de comprobaciones.)
, y esto es un número finito de comprobaciones.)
Pensemos ahora en el problema de factorizar polonomios, digamos con coeficientes en  . Si el grado del polinomio
. Si el grado del polinomio  es menor o igual que 3, entonces es inmediato comprobar que
es menor o igual que 3, entonces es inmediato comprobar que  es irreducible en
es irreducible en  si y solo si tiene alguna raiz en
si y solo si tiene alguna raiz en  . En un vídeo anterior ya vimos que es sencillo saber si un polinomo tiene raíces racionales, luego el problema de factorizar polinomios de grado menor o igual que 3 como producto de polinomios irreducibles es sencillo.
. En un vídeo anterior ya vimos que es sencillo saber si un polinomo tiene raíces racionales, luego el problema de factorizar polinomios de grado menor o igual que 3 como producto de polinomios irreducibles es sencillo.
Supongamos ahora que el grado de  es 4, y que
es 4, y que  no tiene raíces racionales. Entonces
no tiene raíces racionales. Entonces  es irreducible si y solo si no se puede factorizar como el producto de dos polinomios irreducibles de grado 2. Pero, ¿cómo comprobamos si esto es posible o no? Por analogía con el problema de ver si un número es primo o no, podríamos pensar en hacerlo probando con todos los polinomios irreducibles de grado 2: si alguno de estos polinomios de grado 2 divide a
es irreducible si y solo si no se puede factorizar como el producto de dos polinomios irreducibles de grado 2. Pero, ¿cómo comprobamos si esto es posible o no? Por analogía con el problema de ver si un número es primo o no, podríamos pensar en hacerlo probando con todos los polinomios irreducibles de grado 2: si alguno de estos polinomios de grado 2 divide a  entonces
entonces  no es irreducible y en caso contrario sí que lo es. Este argumento es teóricamente correcto, pero hay una diferencia: es sencillo ver que hay infinitos polinomios irreducibles de grado 2 (por ejemplo, todos los de la forma
no es irreducible y en caso contrario sí que lo es. Este argumento es teóricamente correcto, pero hay una diferencia: es sencillo ver que hay infinitos polinomios irreducibles de grado 2 (por ejemplo, todos los de la forma  , con
, con  ).
).
Es decir, saber si un polinomio es irreducible o no es un problema mucho más complicado que saber si un número es primo o no. De hecho, no se conoce ningún criterio general que nos permita determinar si un polinomio dado es irreducible. Hay algunos resultados que nos permiten saberlo en casos particulares. Uno de ellos es el criterio de Eisenstein, que presentamos en el siguiente vídeo.
Cuerpo algebraicamente cerrado
En matemáticas, un cuerpo F se dice algebraicamente cerrado si cada polinomio de grado al menos 1, con coeficientes en F, tiene uncero en F. En ese caso, cada polinomio de tal clase se descompone en factores lineales. Puede demostrarse que un cuerpo es algebraicamente cerrado si no tiene extensiones propias, lo que se toma a veces como definición.
Como ejemplo, el cuerpo de los números reales no es algebraicamente cerrado, ya que el polinomio
no tiene ceros reales. Como contraste, el cuerpo de los números complejos es algebraicamente cerrado: esto es lo que dice el teorema fundamental del álgebra.
Cada cuerpo F tiene una «clausura algebraica», que es el cuerpo algebraicamente cerrado más pequeño del cual F es un subcuerpo. Cada cerradura algebraica de un cuerpo es única salvo isomorfismo. En particular, el cuerpo de los números complejos es la clausura algebraica del cuerpo de los números reales. También tenemos que el cuerpo de los números algebraicos es la clausura algebraica del cuerpo de los números racionales.
Un cuerpo algebraicamente cerrado
Sin embargo, en cierto modo el cuerpo R era decepcionante: una simple ecuación de segundo grado tal como ésta:
x 2+1=0
no tenía soluciones en él.
A nadie se le escapará que no estoy presentando las cosas cronológicamente: era de antiguo conocido que no existen soluciones reales de ecuaciones muy sencillas. Sin embargo el paso siguiente, que consistía en la construcción de un cuerpo algebraicamente cerrado en el cual todo polinomio de coeficientes racionales (o enteros, lo mismo da) tenga solución en su seno, estaba al alcance de la mano. De hecho, intelectualmente la construcción de R fue un reto mucho mayor que la construcción de C , el cuerpo de los números complejos, ya que este surge casi trivialmente con la consideración de pares ordenados (a,b) de números reales si definimos bien las operaciones suma y producto.
Tenemos así un cuerpo numérico algebraicamente cerrado, como nos lo enuncia el merecidamente famoso Teorema fundamental del álgebra , que dice que
todo polinomio a coeficientes complejos tiene un raíz compleja, es decir existe un número complejo donde el polinomio evalua a cero.
Esto es lo mismo que decir que todo polinomio de grado n con coeficientes complejos (o naturales, pues los naturales complejos son); tiene en Cexactamente n soluciones, no necesariamente diferentes.
Efectivamente, si Pn(x) es el polinomio original, el enunciado del teorema asegura la existencia de una raíz w, con lo que podemos expresar el polinomio como:
Pn(x) =(x-w)·Pn-1(x) .
Ahora aplicando lo mismo al nuevo polinomio con un grado menos Pn-1(x)y sucesivamente hasta llegar al polinomio de grado uno, tenemos n raíces, no necesariamente diferentes de Pn(x) en el seno de C .
Particularmente, la ecuación
x n=1
tiene n soluciones en C , ésta vez todas diferentes. Se trata de las denominadas raíces de la unidad .
El estudio de las mismas es una bella y multidisciplinar parcela de la matemática que es: la teoría de variable compleja , la geometría, la teoría de grupos cíclicos y la teoría de polinomios ciclotómicos beben de esta fuente de cristalinas aguas.

No hay comentarios:
Publicar un comentario