Teoría de anillos
anillo conmutativo es un anillo (R, +, ·) en el que la operación de multiplicación · es conmutativa; es decir, si para cualquiera a, b ∈ R, a·b = b·a.
Si adicionalmente el anillo tiene un elemento unitario 1 tal que 1a = a = a1 para todo a, entonces el anillo se denomina anillo conmutativo unitario.
La rama de la teoría de anillos que estudia los anillos conmutativos se denomina álgebra conmutativa.
Ejemplos
- El ejemplo más importante es tal vez el de los números enteros con las operaciones usuales de suma y multiplicación, ambas conmutativas. Este anillo usualmente se denota por Z, por la palabra alemana Zahlen (números).
- Los números racionales, reales, y complejos forman anillos conmutativos con las operaciones usuales; más aún, son campos.
- Más generalmente, todo campo es un anillo conmutativo por definición.
- El mejor ejemplo de un anillo no conmutativo es el conjunto de matrices cuadradas de 2×2 con valores reales. Por ejemplo, la multiplicación matricial
-
- da un resultado distinto que si se invierte el orden de los factores:
- Si n > 0 es un entero, el conjunto Zn de enteros módulo n forma un anillo conmutativo con n elementos.
- Si R es un anillo conmutativo, el conjunto de polinomios de variable X con coeficientes en R forma un nuevo anillo conmutativo, denotado por R[X].
- El conjunto de números racionales de denominador impar forma un anillo conmutativo, estrictamente contenido en el anillo Q de los racionales, y que contiene propiamente al Z de los enteros.
Propiedades
- Si f : R → S es un homomorfismo de anillos entre R y S, S es conmutativo, y f es inyectiva (esto es, un monomorfismo), R también debe ser conmutativo, puesf(a·b) = f(a)·f(b) = f(b)·f(a) = f(b·a).
- Si f : R → S es un homomorfismo de anillos entre R y S, con R es conmutativo, la imagen f(R) de R será también conmutativa; en particular, si f es sobreyectiva(esto es, un epimorfismo), S será conmutativo también.
El mayor interés de los anillos conmutativos está en cuando además son unitarios, es decir, los anillos conmutativos unitarios.
Anillos Conmutativos .- .....................................................:http://personales.unican.es/ruizvc/algebra/anillos1.pdf
álgebra abstracta y teoría de anillos, una colección no vacía de conjuntos  es un anillo (de conjuntos) si es cerrada bajo las operaciones de intersección y diferencia simétrica.
es un anillo (de conjuntos) si es cerrada bajo las operaciones de intersección y diferencia simétrica.
 es un anillo (de conjuntos) si es cerrada bajo las operaciones de intersección y diferencia simétrica.
es un anillo (de conjuntos) si es cerrada bajo las operaciones de intersección y diferencia simétrica.
Formalmente, para cualquier  , debe cumplirse
, debe cumplirse
 , debe cumplirse
, debe cumplirse
donde  representa la diferencia simétrica
representa la diferencia simétrica 
 representa la diferencia simétrica
representa la diferencia simétrica 
Un anillo de conjuntos forma un anillo (posiblemente sin unidad) bajo estas dos operaciones. La intersección se distribuye sobre la diferencia simétrica:

El conjunto vacío es el elemento identidad para  , y la unión de todos los conjuntos, es el elemento identidad para
, y la unión de todos los conjuntos, es el elemento identidad para  , creando un anillo unitario.
, creando un anillo unitario.
 , y la unión de todos los conjuntos, es el elemento identidad para
, y la unión de todos los conjuntos, es el elemento identidad para  , creando un anillo unitario.
, creando un anillo unitario.
Dado cualquier conjunto X, el conjunto potencia de X forma un anillo de conjuntos discreto, mientras que la colección {∅,X} constituye un anillo de conjuntos no discreto. Cualquier campo de conjuntos, así como cualquier sigma-álgebra son también anillos de conjuntos.
Los anillos de conjuntos son retículos distributivos.
Sean  y
y  anillos sobre
anillos sobre  e
e  , respectivamente. La clase
, respectivamente. La clase  , ¿es un anillo sobre
, ¿es un anillo sobre  ?
?
Todo anillo es semianillo por lo que es claro que es un semianillo y contendrá al vacío y será cerrado para la intersección finita. Sin embargo, no siempre es un anillo como podemos ver mediante un contraejemplo. Sean
es un semianillo y contendrá al vacío y será cerrado para la intersección finita. Sin embargo, no siempre es un anillo como podemos ver mediante un contraejemplo. Sean
 ,
,
 .
.
Ambas clases son anillos sobre los naturales. La clase contiene a los conjuntos
contiene a los conjuntos  y
y  . Pero su unión es
. Pero su unión es

Veamos que tal unión no pertenece al producto cartesiano de las clases. Los elementos de son
son
Todo anillo es semianillo por lo que es claro que
Ambas clases son anillos sobre los naturales. La clase
Veamos que tal unión no pertenece al producto cartesiano de las clases. Los elementos de
Pero el conjunto  no es ninguno de ellos como el lector puede comprobar. Así pues, el producto cartesiano de anillos (o de álgebras) no es siempre un anillo (o álgebra).
no es ninguno de ellos como el lector puede comprobar. Así pues, el producto cartesiano de anillos (o de álgebras) no es siempre un anillo (o álgebra).
anillo de división o cuerpo no conmutativo es un anillo unitario en el que todo elemento distinto de cero es invertible y por tanto una unidad. Es decir, si R es un anillo unitario y U(R) es su grupo de unidades,  .
.
 .
.
Todo cuerpo es un anillo de división conmutativo. Es por ello que los anillos de división reciben también el nombre de cuerpos no conmutativos, puesto que esta es la única propiedad que los diferencia. Por el teorema de Wedderburn, todo anillo de división finito es un cuerpo finito.
Ejemplos
El ejemplo más sencillo de un anillo de división en el que no se cumple la propiedad conmutativa del producto es el anillo de los cuaterniones de Hamilton: el conjunto de elementos de la forma
donde  , y los elementos i, j y k se operan según las siguientes reglas:
, y los elementos i, j y k se operan según las siguientes reglas:
 , y los elementos i, j y k se operan según las siguientes reglas:
, y los elementos i, j y k se operan según las siguientes reglas:Propiedades
El centro C de un anillo de división A es un cuerpo. El centro de A contiene a los elementos que conmutan con cualquier elemento de A, y forma un subanillo que contiene elementos distintos de 0, puesto que expresamente contiene al elemento unidad. Los anillos de división se pueden clasificar según su dimensión sobre su centro ![[ A : C ]](https://upload.wikimedia.org/math/3/d/3/3d38df46bc9fa2cd58f1e747d52b251a.png) , cuando la dimensión es finita se dice que A es una extensión finita de C. Todo cuerpo es obviamente unidimensional.1
, cuando la dimensión es finita se dice que A es una extensión finita de C. Todo cuerpo es obviamente unidimensional.1
![[ A : C ]](https://upload.wikimedia.org/math/3/d/3/3d38df46bc9fa2cd58f1e747d52b251a.png) , cuando la dimensión es finita se dice que A es una extensión finita de C. Todo cuerpo es obviamente unidimensional.1
, cuando la dimensión es finita se dice que A es una extensión finita de C. Todo cuerpo es obviamente unidimensional.1
En el ejemplo del anillo de los cuaterniones reales, el centro está formado por todos los elementos de la forma  , y es por tanto isomorfo al cuerpo de los números reales. El anillo de los cuaterniones es cuatro-dimensional respecto de su centro.
, y es por tanto isomorfo al cuerpo de los números reales. El anillo de los cuaterniones es cuatro-dimensional respecto de su centro.
 , y es por tanto isomorfo al cuerpo de los números reales. El anillo de los cuaterniones es cuatro-dimensional respecto de su centro.
, y es por tanto isomorfo al cuerpo de los números reales. El anillo de los cuaterniones es cuatro-dimensional respecto de su centro.
Sea  un anillo (conmutativo y unitario) y
un anillo (conmutativo y unitario) y 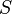 un subconjunto multiplicativamente cerrado de
un subconjunto multiplicativamente cerrado de  . Consideremos en
. Consideremos en  la relación binaria
la relación binaria
 un anillo (conmutativo y unitario) y
un anillo (conmutativo y unitario) y 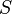 un subconjunto multiplicativamente cerrado de
un subconjunto multiplicativamente cerrado de  . Consideremos en
. Consideremos en  la relación binaria
la relación binaria
Es fácil comprobar que 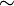 es una relación de equivalencia y, por tanto, puede considerarse el conjunto cociente
es una relación de equivalencia y, por tanto, puede considerarse el conjunto cociente  que denotaremos por
que denotaremos por  . Indicaremos por
. Indicaremos por  o
o  a la clase del elemento
a la clase del elemento  .
.
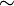 es una relación de equivalencia y, por tanto, puede considerarse el conjunto cociente
es una relación de equivalencia y, por tanto, puede considerarse el conjunto cociente  que denotaremos por
que denotaremos por  . Indicaremos por
. Indicaremos por  o
o  a la clase del elemento
a la clase del elemento  .
.
están bien definidas y dotan a  de una estructura de anillo conmutativo y unitario.
de una estructura de anillo conmutativo y unitario.
 de una estructura de anillo conmutativo y unitario.
de una estructura de anillo conmutativo y unitario.Así se ha construido el anillo de fracciones del anillo
 respecto de
respecto de 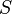 :
:  .
.








No hay comentarios:
Publicar un comentario