Teoría de anillos
anillo de los números enteros se puede referir a
- el anillo de todos los enteros (positivos, negativos o cero), usualmente indicado como Z.
- dado un campo numérico algebraico K, los enteros algebraicos contenidos en K forman un anillo, el anillo de los enteros de K, comúnmente indicado como OK u
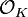 .
.
Usando esta notación, se puede escribir Z = OQ dado que Z es el anillo de enteros del campo Q de números racionales. Y en efecto por esta razón, en la teoría algebraica de números los elementos de Z son comúnmente llamados los "enteros racionales".
El anillo de los números enteros OK tiene una base integral; lo que significa que existe b1,...,bn ∈ OK (la base integral) tal que cada elemento x en OK puede ser unívocamente representado como
con ai ∈ Z.
Si ζ es la p-iésima raíz de la unidad y K=Q(ζ) es el campo ciclotómico correspondiente, entonces una base integral de OK está dada por (1,ζ,ζ2,...,ζp-2).
Si d es un entero cuadrático libre y K=Q(d1/2) es el campo cuadrático correspondiente, entonces una base integral de OK está dada por (1,(1+d1/2)/2) si d≡1 (mod 4) y por (1,d1/2) si d≡2 ó 3 (mod 4).
(1),
en donde  ,
,  ,
,  y cada
y cada  -tupla
-tupla  de números naturales es diferente para diferente valor de
de números naturales es diferente para diferente valor de  , se dice anillo de polinomios con indeterminadas en
, se dice anillo de polinomios con indeterminadas en  sobre
sobre  .
.
 ,
,  ,
,  y cada
y cada  -tupla
-tupla  de números naturales es diferente para diferente valor de
de números naturales es diferente para diferente valor de  , se dice anillo de polinomios con indeterminadas en
, se dice anillo de polinomios con indeterminadas en  sobre
sobre  .
.Introducción
Los polinomios más conocidos son los que tienen coeficientes enteros.
Ejemplo:
El conjunto de indeterminadas  puede ser un conjunto infinito, pero cada polinomio contiene un número finito de términos.[cita requerida]
puede ser un conjunto infinito, pero cada polinomio contiene un número finito de términos.[cita requerida]
 puede ser un conjunto infinito, pero cada polinomio contiene un número finito de términos.[cita requerida]
puede ser un conjunto infinito, pero cada polinomio contiene un número finito de términos.[cita requerida]
Si  , entonces se puede escribir
, entonces se puede escribir ![A[x_1,\ldots, x_n]](https://upload.wikimedia.org/math/e/9/0/e902c25d7b3432c37d030441511a5036.png) en lugar de
en lugar de ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) . Así,
. Así, ![A[x]](https://upload.wikimedia.org/math/f/b/6/fb69d622f2a34064c64bd69b99c1c711.png) es un anillo de polinomios en una sola indeterminada
es un anillo de polinomios en una sola indeterminada  .
.
 , entonces se puede escribir
, entonces se puede escribir ![A[x_1,\ldots, x_n]](https://upload.wikimedia.org/math/e/9/0/e902c25d7b3432c37d030441511a5036.png) en lugar de
en lugar de ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) . Así,
. Así, ![A[x]](https://upload.wikimedia.org/math/f/b/6/fb69d622f2a34064c64bd69b99c1c711.png) es un anillo de polinomios en una sola indeterminada
es un anillo de polinomios en una sola indeterminada  .
.
ya que  , por lo que
, por lo que  es un subanillo de
es un subanillo de ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) .
.
 , por lo que
, por lo que  es un subanillo de
es un subanillo de ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) .
.Propiedades fundamentales
Hechos de interés sobre anillos de polinomios tienen que ver con las propiedades del mismo a partir del anillo en el que tienen sus coeficientes. Por ejemplo, cuando  es un dominio íntegro,
es un dominio íntegro, ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) también lo es, y las unidades de
también lo es, y las unidades de ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) son las mismas que las de
son las mismas que las de  . Por el contrario
. Por el contrario ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) nunca será un cuerpo, no importando que
nunca será un cuerpo, no importando que  lo sea o no, pues aunque las unidades de
lo sea o no, pues aunque las unidades de ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) sean las mismas que las de
sean las mismas que las de  ,
,  es tan sólo un subanillo de
es tan sólo un subanillo de ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) . Sin embargo, el anillo
. Sin embargo, el anillo ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) es un dominio integro si
es un dominio integro si  lo es, luego, dado el caso, se puede construir el cuerpo de cocientes de
lo es, luego, dado el caso, se puede construir el cuerpo de cocientes de ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) (i.e. el cuerpo de fracciones de polinomios), que se denota comúnmente por
(i.e. el cuerpo de fracciones de polinomios), que se denota comúnmente por  .
.
 es un dominio íntegro,
es un dominio íntegro, ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) también lo es, y las unidades de
también lo es, y las unidades de ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) son las mismas que las de
son las mismas que las de  . Por el contrario
. Por el contrario ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) nunca será un cuerpo, no importando que
nunca será un cuerpo, no importando que  lo sea o no, pues aunque las unidades de
lo sea o no, pues aunque las unidades de ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) sean las mismas que las de
sean las mismas que las de  ,
,  es tan sólo un subanillo de
es tan sólo un subanillo de ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) . Sin embargo, el anillo
. Sin embargo, el anillo ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) es un dominio integro si
es un dominio integro si  lo es, luego, dado el caso, se puede construir el cuerpo de cocientes de
lo es, luego, dado el caso, se puede construir el cuerpo de cocientes de ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) (i.e. el cuerpo de fracciones de polinomios), que se denota comúnmente por
(i.e. el cuerpo de fracciones de polinomios), que se denota comúnmente por  .
.
Los coeficientes de los polinomios de un anillo ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) pueden tomarse no solo como los elementos de
pueden tomarse no solo como los elementos de  . En la practica podemos hacer agrupaciones del tipo
. En la practica podemos hacer agrupaciones del tipo
![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) pueden tomarse no solo como los elementos de
pueden tomarse no solo como los elementos de  . En la practica podemos hacer agrupaciones del tipo
. En la practica podemos hacer agrupaciones del tipo
y éstas también deben hacerse en un anillo de polinomios ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) . Para ello se separan los elementos de
. Para ello se separan los elementos de  en dos conjuntos disjuntos, digamos
en dos conjuntos disjuntos, digamos  y
y  , luego el anillo de polinomios
, luego el anillo de polinomios ![A[R][T]](https://upload.wikimedia.org/math/d/b/2/db2ac3cb55fbfcb505eea599c818cb03.png) tiene coeficientes en el anillo de polinomios
tiene coeficientes en el anillo de polinomios ![A[R]](https://upload.wikimedia.org/math/c/4/c/c4c493fe93ba89d783ec0b11ceef110d.png) e indeterminadas en
e indeterminadas en  . Si
. Si  es un anillo y
es un anillo y  , claramente
, claramente ![A[R]](https://upload.wikimedia.org/math/c/4/c/c4c493fe93ba89d783ec0b11ceef110d.png) es un subanillo de
es un subanillo de ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) .
.
![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) . Para ello se separan los elementos de
. Para ello se separan los elementos de  en dos conjuntos disjuntos, digamos
en dos conjuntos disjuntos, digamos  y
y  , luego el anillo de polinomios
, luego el anillo de polinomios ![A[R][T]](https://upload.wikimedia.org/math/d/b/2/db2ac3cb55fbfcb505eea599c818cb03.png) tiene coeficientes en el anillo de polinomios
tiene coeficientes en el anillo de polinomios ![A[R]](https://upload.wikimedia.org/math/c/4/c/c4c493fe93ba89d783ec0b11ceef110d.png) e indeterminadas en
e indeterminadas en  . Si
. Si  es un anillo y
es un anillo y  , claramente
, claramente ![A[R]](https://upload.wikimedia.org/math/c/4/c/c4c493fe93ba89d783ec0b11ceef110d.png) es un subanillo de
es un subanillo de ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) .
.
Sea  un anillo unitario. Todo polinomio no nulo de
un anillo unitario. Todo polinomio no nulo de ![A[x]](https://upload.wikimedia.org/math/f/b/6/fb69d622f2a34064c64bd69b99c1c711.png) cuyo coeficiente director sea una unidad puede dividir euclídeamente a cualquier otro polinomio de
cuyo coeficiente director sea una unidad puede dividir euclídeamente a cualquier otro polinomio de ![A[x]](https://upload.wikimedia.org/math/f/b/6/fb69d622f2a34064c64bd69b99c1c711.png) y el grado del resto es estrictamente menor que el grado de del divisor. Es decir, si
y el grado del resto es estrictamente menor que el grado de del divisor. Es decir, si  y
y  son polinomios de
son polinomios de ![A[x]](https://upload.wikimedia.org/math/f/b/6/fb69d622f2a34064c64bd69b99c1c711.png) no nulos, con el coeficiente director de
no nulos, con el coeficiente director de  una unidad de
una unidad de  , entonces existen polinomios
, entonces existen polinomios  y
y  de
de ![A[x]](https://upload.wikimedia.org/math/f/b/6/fb69d622f2a34064c64bd69b99c1c711.png) tales que
tales que
 un anillo unitario. Todo polinomio no nulo de
un anillo unitario. Todo polinomio no nulo de ![A[x]](https://upload.wikimedia.org/math/f/b/6/fb69d622f2a34064c64bd69b99c1c711.png) cuyo coeficiente director sea una unidad puede dividir euclídeamente a cualquier otro polinomio de
cuyo coeficiente director sea una unidad puede dividir euclídeamente a cualquier otro polinomio de ![A[x]](https://upload.wikimedia.org/math/f/b/6/fb69d622f2a34064c64bd69b99c1c711.png) y el grado del resto es estrictamente menor que el grado de del divisor. Es decir, si
y el grado del resto es estrictamente menor que el grado de del divisor. Es decir, si  y
y  son polinomios de
son polinomios de ![A[x]](https://upload.wikimedia.org/math/f/b/6/fb69d622f2a34064c64bd69b99c1c711.png) no nulos, con el coeficiente director de
no nulos, con el coeficiente director de  una unidad de
una unidad de  , entonces existen polinomios
, entonces existen polinomios  y
y  de
de ![A[x]](https://upload.wikimedia.org/math/f/b/6/fb69d622f2a34064c64bd69b99c1c711.png) tales que
tales que | con |  |
Así, para que la división de polinomios sea siempre posible en un anillo de polinomios ![A[x]](https://upload.wikimedia.org/math/f/b/6/fb69d622f2a34064c64bd69b99c1c711.png) ,
,  debe de ser un cuerpo (i.e. todo elemento de A debe ser una unidad), y si así sucede
debe de ser un cuerpo (i.e. todo elemento de A debe ser una unidad), y si así sucede ![A[x]](https://upload.wikimedia.org/math/f/b/6/fb69d622f2a34064c64bd69b99c1c711.png) será un dominio euclídeo. Un hecho muy importante es que un anillo de polinomios
será un dominio euclídeo. Un hecho muy importante es que un anillo de polinomios ![A[x]](https://upload.wikimedia.org/math/f/b/6/fb69d622f2a34064c64bd69b99c1c711.png) es un dominio de ideales principales (DIP) si y sólo si
es un dominio de ideales principales (DIP) si y sólo si  es un cuerpo. Puesto que todos los dominios euclídeos son DIPs, tenemos que
es un cuerpo. Puesto que todos los dominios euclídeos son DIPs, tenemos que ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) no es un dominio euclídeo si
no es un dominio euclídeo si  contiene más de un elemento, pues
contiene más de un elemento, pues ![A[S]=A[S\setminus\{x\}][x]](https://upload.wikimedia.org/math/d/d/4/dd467f262e82de193713e7e451c1c0d2.png) , y
, y ![A[S\setminus\{x\}]](https://upload.wikimedia.org/math/6/a/b/6ab3588926507b0a79f80965e721892d.png) nunca es un cuerpo y por tanto tampoco un DIP.
nunca es un cuerpo y por tanto tampoco un DIP.
![A[x]](https://upload.wikimedia.org/math/f/b/6/fb69d622f2a34064c64bd69b99c1c711.png) ,
,  debe de ser un cuerpo (i.e. todo elemento de A debe ser una unidad), y si así sucede
debe de ser un cuerpo (i.e. todo elemento de A debe ser una unidad), y si así sucede ![A[x]](https://upload.wikimedia.org/math/f/b/6/fb69d622f2a34064c64bd69b99c1c711.png) será un dominio euclídeo. Un hecho muy importante es que un anillo de polinomios
será un dominio euclídeo. Un hecho muy importante es que un anillo de polinomios ![A[x]](https://upload.wikimedia.org/math/f/b/6/fb69d622f2a34064c64bd69b99c1c711.png) es un dominio de ideales principales (DIP) si y sólo si
es un dominio de ideales principales (DIP) si y sólo si  es un cuerpo. Puesto que todos los dominios euclídeos son DIPs, tenemos que
es un cuerpo. Puesto que todos los dominios euclídeos son DIPs, tenemos que ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) no es un dominio euclídeo si
no es un dominio euclídeo si  contiene más de un elemento, pues
contiene más de un elemento, pues ![A[S]=A[S\setminus\{x\}][x]](https://upload.wikimedia.org/math/d/d/4/dd467f262e82de193713e7e451c1c0d2.png) , y
, y ![A[S\setminus\{x\}]](https://upload.wikimedia.org/math/6/a/b/6ab3588926507b0a79f80965e721892d.png) nunca es un cuerpo y por tanto tampoco un DIP.
nunca es un cuerpo y por tanto tampoco un DIP.Definición formal
Los monomios puros
La definición formal de los anillos de polinomios parte de la definición de los monomios puros (sin coeficientes en un anillo; en muchos contextos, la palabra monomiocorresponde a este significado, utilizándose entonces la palabra término para designar el producto de un coeficiente del anillo y un monomio). Notar que si  es un conjunto y, por ejemplo,
es un conjunto y, por ejemplo,  , un monomio a partir de
, un monomio a partir de  puede ser
puede ser
 es un conjunto y, por ejemplo,
es un conjunto y, por ejemplo,  , un monomio a partir de
, un monomio a partir de  puede ser
puede ser(3).
En el monomio anterior, cada uno de los elementos  tiene un exponente natural. Por tanto, podemos considerar a cada monomio con indeterminadas en
tiene un exponente natural. Por tanto, podemos considerar a cada monomio con indeterminadas en  como una aplicación
como una aplicación  (aquí y en el resto del artículo consideramos que
(aquí y en el resto del artículo consideramos que  incluye al cero). El monomio () sería entendido entonces como la aplicación
incluye al cero). El monomio () sería entendido entonces como la aplicación  dada por
dada por  ,
,  ,
,  y donde
y donde  se anula para todos los demás elementos (si estos existen) de
se anula para todos los demás elementos (si estos existen) de  . Observar que un monomio puro es elproducto de un número finito de indeterminadas. Aunque
. Observar que un monomio puro es elproducto de un número finito de indeterminadas. Aunque  sea infinito, podemos obtener un monomio
sea infinito, podemos obtener un monomio  haciendo que
haciendo que  sea nulo para todas aquellas indeterminadas que no queremos que aparezcan en el monomio. Por ejemplo, si
sea nulo para todas aquellas indeterminadas que no queremos que aparezcan en el monomio. Por ejemplo, si 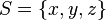 , el monomio
, el monomio
 tiene un exponente natural. Por tanto, podemos considerar a cada monomio con indeterminadas en
tiene un exponente natural. Por tanto, podemos considerar a cada monomio con indeterminadas en  como una aplicación
como una aplicación  (aquí y en el resto del artículo consideramos que
(aquí y en el resto del artículo consideramos que  incluye al cero). El monomio () sería entendido entonces como la aplicación
incluye al cero). El monomio () sería entendido entonces como la aplicación  dada por
dada por  ,
,  ,
,  y donde
y donde  se anula para todos los demás elementos (si estos existen) de
se anula para todos los demás elementos (si estos existen) de  . Observar que un monomio puro es elproducto de un número finito de indeterminadas. Aunque
. Observar que un monomio puro es elproducto de un número finito de indeterminadas. Aunque  sea infinito, podemos obtener un monomio
sea infinito, podemos obtener un monomio  haciendo que
haciendo que  sea nulo para todas aquellas indeterminadas que no queremos que aparezcan en el monomio. Por ejemplo, si
sea nulo para todas aquellas indeterminadas que no queremos que aparezcan en el monomio. Por ejemplo, si 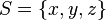 , el monomio
, el monomio(4),
En vista de las consideraciones anteriores, la definición de un conjunto de monomios ha de ser la siguiente:
|
Si
 , se definen las aplicaciones
, se definen las aplicaciones  y
y  , donde
, donde  , mediante
, mediante | y |  |
para todo  .
.
 .
.Estas aplicaciones están bien definidas, y claramente
 y y
y y  . Vemos pues que si
. Vemos pues que si  son aplicaciones de
son aplicaciones de  ,
,  se interpreta como elproducto de los monomios representados por
se interpreta como elproducto de los monomios representados por  y
y  , y si
, y si  es un número natural,
es un número natural,  se interpreta como la potencia
se interpreta como la potencia  -sima del monomio representado por
-sima del monomio representado por  .
.Nótese que el monomio
 de
de  que toma constantemente el valor 0 es tal que
que toma constantemente el valor 0 es tal que | y |  |
para todo  . Así, este monomio se representa por el mismo símbolo 0.
. Así, este monomio se representa por el mismo símbolo 0.
 . Así, este monomio se representa por el mismo símbolo 0.
. Así, este monomio se representa por el mismo símbolo 0.Obsérvese que el elemento
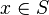 se interpreta en
se interpreta en  , claramente, como la aplicación
, claramente, como la aplicación  que vale 1 en
que vale 1 en  y 0 en cualquier otro caso. En estos términos cualquier monomio
y 0 en cualquier otro caso. En estos términos cualquier monomio  de
de  puede escribirse como
puede escribirse como(5),
donde  son los elementos de
son los elementos de  para los cuales la aplicación
para los cuales la aplicación  no se anula (por definición, estos elementos son siempre un número finito). Claramente, cada término
no se anula (por definición, estos elementos son siempre un número finito). Claramente, cada término
 son los elementos de
son los elementos de  para los cuales la aplicación
para los cuales la aplicación  no se anula (por definición, estos elementos son siempre un número finito). Claramente, cada término
no se anula (por definición, estos elementos son siempre un número finito). Claramente, cada término(6)
de () representa el factor  en el monomio representado por
en el monomio representado por  . Es decir, () se entiende como el monomio
. Es decir, () se entiende como el monomio
 en el monomio representado por
en el monomio representado por  . Es decir, () se entiende como el monomio
. Es decir, () se entiende como el monomio(7)
Polinomios con coeficientes en un anillo
Para dar paso a la definición de un anillo de polinomios, observemos que un polinomio, como (), es una suma finita de monomios multiplicados por coeficientes en unanillo (en el caso de () los coeficientes son enteros). Así, por ejemplo, es suficiente asociar el polinomio () con una aplicación  , donde
, donde  , tal que
, tal que  toma el valor del coeficiente correspondiente cuando se evalúa en un monomio
toma el valor del coeficiente correspondiente cuando se evalúa en un monomio  . En vista de esto tenemos:
. En vista de esto tenemos:
 , donde
, donde  , tal que
, tal que  toma el valor del coeficiente correspondiente cuando se evalúa en un monomio
toma el valor del coeficiente correspondiente cuando se evalúa en un monomio  . En vista de esto tenemos:
. En vista de esto tenemos:
|
Podemos considerar ahora los monomios con coeficientes en el anillo  como casos especiales de polinomios. Si
como casos especiales de polinomios. Si  es unitario, entonces podemos considerar al polinomio
es unitario, entonces podemos considerar al polinomio  que vale 1 en
que vale 1 en  y 0 en cualquier otro caso como el monomio
y 0 en cualquier otro caso como el monomio  mismo. Para ver que, en realidad, tanto
mismo. Para ver que, en realidad, tanto  como
como  son, desde el punto de vista algebraico, un subconjunto de
son, desde el punto de vista algebraico, un subconjunto de ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) y que efectivamente
y que efectivamente ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) es un anillo que contiene a
es un anillo que contiene a  como un subanillo, es necesario definir las operaciones de anillo sobre
como un subanillo, es necesario definir las operaciones de anillo sobre ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) .
.
 como casos especiales de polinomios. Si
como casos especiales de polinomios. Si  es unitario, entonces podemos considerar al polinomio
es unitario, entonces podemos considerar al polinomio  que vale 1 en
que vale 1 en  y 0 en cualquier otro caso como el monomio
y 0 en cualquier otro caso como el monomio  mismo. Para ver que, en realidad, tanto
mismo. Para ver que, en realidad, tanto  como
como  son, desde el punto de vista algebraico, un subconjunto de
son, desde el punto de vista algebraico, un subconjunto de ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) y que efectivamente
y que efectivamente ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) es un anillo que contiene a
es un anillo que contiene a  como un subanillo, es necesario definir las operaciones de anillo sobre
como un subanillo, es necesario definir las operaciones de anillo sobre ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) .
.
Operaciones sobre ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png)
Definiciones
La adición sobre ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) claramente ha de definirse así:
claramente ha de definirse así:
![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) claramente ha de definirse así:
claramente ha de definirse así:
|
Esta definición se interpreta como la reducción de los términos semejantes (i.e. los coeficientes de un mismo monomio
 ) de
) de  y
y  .
.Cuando multiplicamos polinomios, acostumbramos sumar los términos semejantes que surjan en el producto para obtener un polinomio lo más reducido posible. En vista de esto, tenemos la definición de la multiplicación en
![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) :
:
|
Propiedades de anillo
Respecto de las operaciones de adición y multiplicación, según han sido definidas, el conjunto ![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) cumple con que:
cumple con que:
![A[S]](https://upload.wikimedia.org/math/1/6/3/163f50da6ac380b4221607faa48735f3.png) cumple con que:
cumple con que:
ANILLOS DE POLINOMIOS .- .....................................................................:http://www.instituto127.com.ar/Academicos/Catedras/ProfMate_algebra/3_Anillos_de_polinomios.pdf Anillo de polinomios. Divisi´on y factorizaci´on. Lema de Gauss. - ......................................:http://euclides.us.es/da/apuntes/algebra/t6-2004-05.pdf ANILLOS DE POLINOMIOS .- ...................................................:http://www.ual.es/~btorreci/polinomi.pdf |

 y
y ![\mathbb{Z}[S]](https://upload.wikimedia.org/math/7/e/d/7ed74b23160bc061ba1f43ac9ce248dc.png) es un polinomio de dos variables como:
es un polinomio de dos variables como:
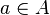 le corresponde un
le corresponde un 

 ,
,  y
y  .
. es finito.
es finito.

 tales que el conjunto
tales que el conjunto  es finito.
es finito.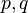 polinomios de
polinomios de 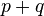 como la aplicación dada por
como la aplicación dada por
![p+q\in A[S]](https://upload.wikimedia.org/math/6/9/1/691456ba943198a9df26351f786f7b50.png) .
. como la aplicación dada por
como la aplicación dada por
 tales que
tales que  . La aplicación
. La aplicación
No hay comentarios:
Publicar un comentario