artiniano por la izquierda si sus ideales por la izquierda satisfacen la condición de cadena descendente. Diremos que un anillo es artiniano si es artiniano por la izquierda y por la derecha. En los anillos conmutativos no se utiliza esta distinción, pues artiniano por un lado implica artiniano por el otro. Si un anillo es artiniano, entonces es noetheriano.
Resultados conocidos
Si R es un anillo artiniano y J su radical de Jacobson, entonces R/J es semisimple y J es nilpotente.
Todo anillo artiniano es perfecto. Esto implica toda una serie de buenas propiedades como que todo módulo tiene una cubierta proyectiva, así como que el límite directo de módulos proyectivos es proyectivo. También se verifica que todo módulo plano es proyectivo.
Ejemplos
a) Los cuerpos y anillos de división.
b) Los anillos conmutativos en los que cada ideal primo es maximal
c) El anillo de las matrices de orden n sobre un cuerpo (teorema de Artin-Wedderburn)
d) Todo anillo noetheriano cuyo radical sea nilpotente.
b) Los anillos conmutativos en los que cada ideal primo es maximal
c) El anillo de las matrices de orden n sobre un cuerpo (teorema de Artin-Wedderburn)
d) Todo anillo noetheriano cuyo radical sea nilpotente.
anillo booleano es aquel anillo R en donde  para todo elemento de R.
para todo elemento de R.
 para todo elemento de R.
para todo elemento de R.
Expresado de otra forma, es un anillo en el que todos los términos son idempotentes.
Conmmutatividad de los anillos booleanos
Los anillos booleanons necesariamente son anillos conmutativos.
Un error común para demostrar esta propiedad es establecer la igualdad abab = aabb y posteriormente "cancelar" a y b por ambos lados. Esto es incorrecto ya que a diferencia de un campo, los elementos de un anillo no tienen necesariamente inversos multiplicativos y por tanto no es posible hacer cancelaciones.
A continuación se presenta una prueba correcta de la conmutatividad.
| Los anillos booleanos son conmutativos |
| Sean a y b dos elementos arbitrarios del anillo booleano R.
Primero observamos que necesariamente todo elemento es su propio inverso aditivo:
de donde una cancelación muestra que
 y por tanto y por tanto  . .
Dado que
 , desarrollando el producto del lado derecho obtenemos: , desarrollando el producto del lado derecho obtenemos:
de donde se obtiene que
 y por tanto y por tanto  , de donde ya es inmediato que , de donde ya es inmediato que  , estableciéndose así la conmutatividad del anillo. , estableciéndose así la conmutatividad del anillo. |
Equivalencia entre anillos booleanos y álgebras booleanas
Todo anillo booleano 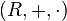 con elemento unitario 1 satisface los axiomas de un álgebra booleana
con elemento unitario 1 satisface los axiomas de un álgebra booleana  si se define la disyunción como:
si se define la disyunción como:
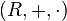 con elemento unitario 1 satisface los axiomas de un álgebra booleana
con elemento unitario 1 satisface los axiomas de un álgebra booleana  si se define la disyunción como:
si se define la disyunción como:,
la conjunción como:
y la negación como:
.
De manera inversa, toda álgebra booleana se puede convertir en un anillo conmutativo definiendo las operaciones de suma y producto como:
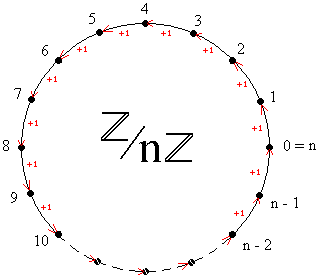
Los anillos cíclicos se caracterizan por ser generados por un sólo elemento (se dicen monogéneos) y por ser finitos. Más precisamente, para todo número natural n ≥ 2 existe un único anillo cíclico (mediante isomorfismos) de orden (tamaño) n, se lo nota Z/nZ(como cociente del anillo Z por el ideal nZ), Z/(n) (nZ, ideal generado por nse escribe también (n) ) o Zn, y se puede representar como en la figura.
Fueron los primeros anillos descubiertos después de Z y la apelación "anillo" proviene evidentemente de la figura anterior.
Fueron los primeros anillos descubiertos después de Z y la apelación "anillo" proviene evidentemente de la figura anterior.
Cálculo elemental
En el anillo Zn, la suma y el producto son los usuales en Z con una regla adicional: se decide que los números n y 0 son iguales: se escribe n ≡ 0 ó n ≡ 0 (mod n) para ser más preciso, cuando uno se sitúa en Z, y  cuando se trabaja en Zn (ā es una manera arbitraria de designar la clase de equivalencia de a en Zn - no se empleará aquí esta notación).
cuando se trabaja en Zn (ā es una manera arbitraria de designar la clase de equivalencia de a en Zn - no se empleará aquí esta notación).
Aplicando varias veces lo anterior se muestra que es lícito añadir o sustraer cuantas veces se quiere "n" a un término sin cambiar su valor en Zn :
 cuando se trabaja en Zn (ā es una manera arbitraria de designar la clase de equivalencia de a en Zn - no se empleará aquí esta notación).
cuando se trabaja en Zn (ā es una manera arbitraria de designar la clase de equivalencia de a en Zn - no se empleará aquí esta notación).Aplicando varias veces lo anterior se muestra que es lícito añadir o sustraer cuantas veces se quiere "n" a un término sin cambiar su valor en Zn :
Se dice que a y a + k·n son iguales módulo n o congruentes módulo n y se llama cálculo modular o congruencias esta clase de igualdades.
Por ejemplo en Z10: 1968 ≡ 8, porque 1968 = 196×10 + 8.
En este ejemplo, 8 es el resto de la división euclidiana de 1968 por 10, y de hecho cada división da lugar a una congruencia:
si a = b·q + r, entonces r ≡ a (mod q)
La relación ≡ se puede ver como una congruencia en Z o como una igualdad en Zn. Como hemos decidido no distinguir el entero a de su clase ā, una misma relación a ≡ b (mod n) tiene dos interpretaciones. Verla como una igualdad conlleva la ventaja de ser mucho más intuitivo; por ejemplo las propiedades siguientes no sorprenderán:
Sean a1,a2, b1, b2 enteros (o elementos de Zn), y m un natural, entonces:
Sean a1,a2, b1, b2 enteros (o elementos de Zn), y m un natural, entonces:

Aplicaciones directas a la aritmética
- Los criterios de divisibilidad por 3, 9 y 11 son consecuencia directa de la relaciones anteriores.
Consideremos el más conocido, el criterio por 9. Sea un número ncuyas cifras son ao (unidades), a1 (decenas), a2 (centenares)...
Es costumbre escribirlo  para distinguirlo del producto
para distinguirlo del producto  y vale, en escritura clásica:
y vale, en escritura clásica: 
 para distinguirlo del producto
para distinguirlo del producto  y vale, en escritura clásica:
y vale, en escritura clásica: 
Como  entonces para todo k entero positivo
entonces para todo k entero positivo  , y sumando los términos que aparecen en n se obtiene:
, y sumando los términos que aparecen en n se obtiene: 
 entonces para todo k entero positivo
entonces para todo k entero positivo  , y sumando los términos que aparecen en n se obtiene:
, y sumando los términos que aparecen en n se obtiene: 
Es decir que el resto módulo 9 se obtiene sumando las cifras del número. Para verificar un cálculo, por ejemplo un producto: a = b×c, se miran los restos módulo 9, a', b' y c', y si a'≠b'×c' (mod 9) entonces el cálculo es erróneo. En caso contrario no se puede concluir.
- Las congruencias permiten también resolver problemillos esencialmente lúdicos al estilo hallar la cifra de las unidades de 20032005.
Un ordenador común y corriente es incapaz de calcular tamaño número. Buena ocasión para subrayar la superioridad de la inteligencia humana sobre la artificial, y lucirse a la primera oportunidad...
Encontrar la cifra de las unidades se logra trabajando módulo 10, pues el resto de la división por 10 es justamente esta cifra.
Como 2003 ≡ 3 (mod 10), 20032005 ≡ 32005, luego nos toca mirar los 3k (mod 10):
30 ≡ 1, 3¹ ≡ 3, 3² ≡ 3, 3³ = 27 ≡ 7, 34 = 81 ≡ 1.
Este último resultado permite generalizar: 34k ≡ 1, para todo k natural.
Luego dividimos 2005 por 4: 2005 = 4×501 + 1.
Finalmente 32005 = 34×501 + 1 = 34×501× 3¹ ≡ 1 × 3 = 3 (mod 10).
La cifra buscada es 3.
Encontrar la cifra de las unidades se logra trabajando módulo 10, pues el resto de la división por 10 es justamente esta cifra.
Como 2003 ≡ 3 (mod 10), 20032005 ≡ 32005, luego nos toca mirar los 3k (mod 10):
30 ≡ 1, 3¹ ≡ 3, 3² ≡ 3, 3³ = 27 ≡ 7, 34 = 81 ≡ 1.
Este último resultado permite generalizar: 34k ≡ 1, para todo k natural.
Luego dividimos 2005 por 4: 2005 = 4×501 + 1.
Finalmente 32005 = 34×501 + 1 = 34×501× 3¹ ≡ 1 × 3 = 3 (mod 10).
La cifra buscada es 3.
Elementos inversibles
La adición, sustracción y multiplicación se comportan como era de esperar en los anillos cíclicos. Pero ¿ Qué hay de la división ?
Dividir por un número es por definición multiplicar por su inverso. La cuestión es entonces averiguar cuales son los elementos inversibles del anillo. El número a es inversible en Z/(n) si y sólo si existe b tal que:
Dividir por un número es por definición multiplicar por su inverso. La cuestión es entonces averiguar cuales son los elementos inversibles del anillo. El número a es inversible en Z/(n) si y sólo si existe b tal que:
-
- a·b ≡ 1 (mod n) lo que se escribe: a·b = 1 + k·n, k ∈ Z es decir: a·b - k·n = 1.
Esto es una identidad de Bézout y tiene soluciones si y sólo si a y n son números coprimos (es decir primos entre sí: su máximo común divisor es 1 ).
Ejemplos:
Ejemplos:
- 2 y 5, al ser número primos distintos, son coprimos, entonces 2 es inversible en Z5. Una relación de Bézout es 2×3 - 1×5 = 1 que da 2×3 ≡ 1 (mod 5), por lo consiguiente el inverso de 2 es 3 en Z5. En efecto 2×3 = 6 ≡ 1 (mod 5).
- 7 y 12 son coprimos porque el número primo 7 no aparece en la descomposición en factores primos de 12 = 2²×3.
El algoritmo de Euclides permite obtener la relación de Bezout:
-
- 3×12 - 5×7 = 1 que da la congruencia: -5×7 ≡ 1 (mod 12).
-5 es por lo tanto el inverso de 7 en Z12. Pero -5 ≡ 7 (mod 12), por lo consiguiente 7 es su propio inverso en Z12, lo que se verifica rápidamente: 7² = 49 = 4×12 + 1 ≡ 1 (mod 12).
El número de elemento inversibles de Zn se nota φ(n), donde φ es la función fi de Euler.
Si n es primo, y sólo en este caso, todos los enteros naturales no nulos inferiores a n son coprimos con n; esto implica que serán todos inversible en Zn, lo que convierte este anillo en un cuerpo a veces denotado Fn.
El número de elemento inversibles de Zn se nota φ(n), donde φ es la función fi de Euler.
Si n es primo, y sólo en este caso, todos los enteros naturales no nulos inferiores a n son coprimos con n; esto implica que serán todos inversible en Zn, lo que convierte este anillo en un cuerpo a veces denotado Fn.
Universalidad de los anillos cíclicos
Sea A un anillo finito, cuyo neutro (para la multiplicación) denotamos e. El conjunto de los múltiplos de e, C = {0, e, 2·e, 3·e, 4·e...} por ser incluido en A es también finito. Entonces a partir de cierto valor de m, m·e ya fue listado en C, es decir que existe k < m tal que k·e = m·e. Por sustracción n·e = 0 con n = m - k.
Sea n el menor entero natural no nulo tal que n·e = 0. Luego C = {0, e, 2·e, 3·e, 4·e...(n-1)·e} es decir que C es isomorfo al anillo cíclico de orden n. Además Cpertenece al centro de A, pues sus elementos conmuten con todos los de A.
El número n verifica además la propiedad de anular todos los elementos de A: para todo a ∈ A, n·a = n·e·a = 0·a = 0. Es el menor natural no nulo que tiene esta propiedad, y recibe el nombre de característica del anillo.
Sea n el menor entero natural no nulo tal que n·e = 0. Luego C = {0, e, 2·e, 3·e, 4·e...(n-1)·e} es decir que C es isomorfo al anillo cíclico de orden n. Además Cpertenece al centro de A, pues sus elementos conmuten con todos los de A.
El número n verifica además la propiedad de anular todos los elementos de A: para todo a ∈ A, n·a = n·e·a = 0·a = 0. Es el menor natural no nulo que tiene esta propiedad, y recibe el nombre de característica del anillo.
En resumen:
Todo anillo finito tiene en su centro un anillo cíclico.
Su orden es la característica del anillo
La estructura del anillo es definida en gran medida por su anillo cíclico
Su orden es la característica del anillo
La estructura del anillo es definida en gran medida por su anillo cíclico
En efecto, el producto :


Convierte en anillo A en un módulo sobre C = Zn. en particular, si la característica n es un primo, entonces A es un espacio vectorial sobre el cuerpo C = Zn, y como tal es forzosamente ismorfo a Cn. El producto interior le da además una estructura de álgebra.
Productos de anillos cíclicos
Teorema:
Para todo par (a, b) de enteros coprimos, Za·b es isomorfo al producto de anillos Za×Zb.
Esta permite descomponer un anillo cíclico Zn en otros menores, según la factorización en números primos de n.
Prueba:
Consideremos la aplicación lineal f:
-
-
- Z → Za× Zb
- n → (n mod a, n mod b) ("n mod a" es la clase de n en Za)
-
El núcleo de esta aplicación es el conjunto de los n divisibles a la vez por a y por b; son por lo tanto los múltiplos de mínimo común múltiplo de a y b que es ab porque a y b son coprimos: El núcleo es Ker f = a·bZ.
Como a y b son coprimos, el teorema de los restos chinos, consecuencia de la identidad de Bézout afirma que f es sobreyectiva: Im f = Za×Zb. Según la descomposición de una aplicación lineal existe un isomorfismo (luego una biyección) entre Z/Ker f e Im f es decir entre Za·b y Za× Zb.
Como a y b son coprimos, el teorema de los restos chinos, consecuencia de la identidad de Bézout afirma que f es sobreyectiva: Im f = Za×Zb. Según la descomposición de una aplicación lineal existe un isomorfismo (luego una biyección) entre Z/Ker f e Im f es decir entre Za·b y Za× Zb.
La biyección se obtiene gráficamente en un tablero de a × b casillas, enumerando las casillas de la diagonal (lo que corresponde a la aplicación n → (n, n) ) y cuando se alcanza un borde se sigue por el borde opuesto, como si se tocasen. Las flechas en rojo de la segunda figura indican estos repentinos cambios de bordes.
Miremos por ejemplo la casilla que contiene el número 17. Corresponde al elemento de Z28. Está situado en la columna
de Z28. Está situado en la columna 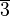 y la fila
y la fila  .
.
Entonces de Z28 corresponde a
de Z28 corresponde a  de Z7×Z4.
de Z7×Z4.
Miremos por ejemplo la casilla que contiene el número 17. Corresponde al elemento
 de Z28. Está situado en la columna
de Z28. Está situado en la columna 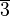 y la fila
y la fila  .
.Entonces
 de Z28 corresponde a
de Z28 corresponde a  de Z7×Z4.
de Z7×Z4.Con valores pequeños de a y b existe otra manera de obtener la biyección: En vez de cortar en pedazos la diagonal, se prefiere reproducir el tablero a × b cuantas veces sea necesario (de hecho, b·a veces) para obtener los a·b elementos de Za·b. Luego se los reúnen en un mismo cuadro.
Z6 ≡ Z2×Z3, así:
0 → (0,0)
1 → (1,1)
2 → (0,2)
3 → (1,0)
4 → (0,1)
5 → (1,2)
anillo cociente, anillo factor o anillo de residuos es el anillo que se obtiene sobre el conjunto de clases de equivalencia de un anillo respecto a una relación de equivalencia  dada por
dada por  donde I es cualquier ideal bilateral cuando las operaciones en el conjunto de clases de equivalencia son inducidas por las operaciones en el anillo original.
donde I es cualquier ideal bilateral cuando las operaciones en el conjunto de clases de equivalencia son inducidas por las operaciones en el anillo original.
 dada por
dada por  donde I es cualquier ideal bilateral cuando las operaciones en el conjunto de clases de equivalencia son inducidas por las operaciones en el anillo original.
donde I es cualquier ideal bilateral cuando las operaciones en el conjunto de clases de equivalencia son inducidas por las operaciones en el anillo original.
Es importante diferenciar el concepto de anillo cociente del de anillos de cocientes, obtenidos por un proceso de localización de un anillo.
Definición formal
Dado un anillo R y un ideal bilateral de R, I. Dado que la estructura aditiva de R es de grupo abeliano, el conjunto  de clases laterales aditivas
de clases laterales aditivas 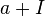 (con
(con  ) adquiere la estructura de grupo abeliano (bajo la operación grupo cociente) mediante la suma de clases laterales definida como:
) adquiere la estructura de grupo abeliano (bajo la operación grupo cociente) mediante la suma de clases laterales definida como:
 de clases laterales aditivas
de clases laterales aditivas 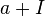 (con
(con  ) adquiere la estructura de grupo abeliano (bajo la operación grupo cociente) mediante la suma de clases laterales definida como:
) adquiere la estructura de grupo abeliano (bajo la operación grupo cociente) mediante la suma de clases laterales definida como:.
Este grupo abeliano adquiere estructura de anillo si adicionalmente se define el producto de clases laterales como
.
- Se establece que el producto está unívocamente determinado, no depende de la elección de los representantes de cada clase. 1
A la estructura de anillo obtenida en  mediante este proceso se le denomina anillo cociente de R entre I.2
mediante este proceso se le denomina anillo cociente de R entre I.2
 mediante este proceso se le denomina anillo cociente de R entre I.2
mediante este proceso se le denomina anillo cociente de R entre I.2Teoremas de isomorfismo
|







 es un
es un  y sea
y sea  es un ideal contenido en
es un ideal contenido en  al anillo de residuos
al anillo de residuos  entonces:
entonces: tal que
tal que  donde
donde  es la proyección canónica de
es la proyección canónica de  en
en  entonces
entonces  .
.
No hay comentarios:
Publicar un comentario