Teoría de anillos
anillo es un sistema algebraico formado por un conjunto no vacío y dos operaciones internas, llamadas usualmente «suma» y «producto», que cumplen ciertas propiedades.
En términos más específicos, se define a la terna (A,+,•) como anillo si (A,+) es un grupo abeliano y • es una operación asociativa y distributiva respecto de +. Suele denominarse «suma» y «producto» a las operaciones + y •, respectivamente. En esta convención, el elemento neutro de la suma se designa como 0 y el inverso con respecto a la suma de un elemento a, perteneciente al conjunto A dado, se denota como –a.
El producto en un anillo no necesariamente tiene una operación inversa definida1 , a diferencia de otras estructuras algebraicas como el cuerpo. Si el producto esconmutativo, tal anillo se denomina «anillo conmutativo». Además, si existe un elemento neutro para el producto, se dice que el anillo es unitario ya que, en este caso, se emplea el número 1 para designar al elemento neutro del producto.
Historia
La teoría de anillos surgió de la exploración de asuntos vinculados con la divisibilidad entre números enteros, del estudio simultáneo de divisibilidad de polinomios y hasta del caso de los cuerpos, concretamente, de los números racionales, números reales, números complejos y de los números algebraicos, de los cuaterniones, fracciones racionales y otros. En la etapa inicial, fueron las materias de de la teoría de números y de la geometría algebraica las que propiciaron los conceptos de anillo, cuerpo e ideal. En su estructuración axiomatica , tales ideas fueron fruto del esfuerzo de Dedekind y otros matemáticos a fines del siglo XIX. Sus aplicaciones al analisis matemático muestran los enfoques modernos de algebrización de tal disciplina matemática, que ocurren recién en el segundo cuarto del siglo XX. 2
Noción de anillo
Véase también: Propiedades de los números enteros
Considérese el conjunto de números enteros:
- ... –8, –3, –2, –1, 0, 1, 2, 3, 8, ...
provisto de dos de las operaciones binarias: la adición y la multiplicación conocidas desde la matemática escolar. Históricamente, el conjunto ℤ de los enteros con sus dos operaciones sirvió de base para la formulación del concepto de anillo[cita requerida]. La razón por la cual los enteros forman un anillo es que poseen las siguientes propiedades:
- Los números enteros están cerrados bajo la suma: dados dos números enteros a y b, se cumple que a + b es un número entero.
- La suma es asociativa: dados tres números enteros a, b y c, se cumple que (a + b) + c = a + (b + c).
- Existe un elemento neutro para la suma: para todo número entero a, a + 0 = 0 + a = a.
- Existe un elemento simétrico para la suma: para todo número entero a, siempre existe algún número entero b, tal que a + b = 0.
- La suma es conmutativa: dados dos números enteros a y b, se cumple que a + b = b + a.
- Los números enteros están cerrados bajo la multiplicación: dados dos números enteros a y b, se cumple que a × b es un número entero.
- La multiplicación es asociativa: dados tres números enteros a, b y c, se cumple que (a × b) × c = a × (b × c).
- Existe un elemento neutro para la multiplicación: para todo número entero a, a × 1 = a.
- La multiplicación es distributiva respecto de la suma: a × (b + c) = (a × b) + (a × c).
Definición
Sea A un conjunto no vacío, y sean  y
y  dos operaciones binarias en A. Se dice que el conjunto
dos operaciones binarias en A. Se dice que el conjunto  es un anillo si se cumplen las siguientes propiedades:
es un anillo si se cumplen las siguientes propiedades:
 y
y  dos operaciones binarias en A. Se dice que el conjunto
dos operaciones binarias en A. Se dice que el conjunto  es un anillo si se cumplen las siguientes propiedades:
es un anillo si se cumplen las siguientes propiedades:1. A es cerrado bajo la operación  .
.
2. La operación  es asociativa.
es asociativa.
3. La operación  tiene a n como elemento neutro.
tiene a n como elemento neutro.
4. Existe un elemento simétrico para  .
.
Estas cuatro condiciones definen un grupo. Una quinta condición define un grupo abeliano:
5. La operación  es conmutativa.
es conmutativa.
Para definir un anillo, es necesario agregar tres condiciones más que hablan acerca de la segunda operación binaria:
6. A es cerrado bajo la operación  .
.
7. La operación  es asociativa.
es asociativa.
8. La operación  es distributiva respecto de
es distributiva respecto de  .
.
Y agregando una novena condición, se define un anillo conmutativo:
9. La operación  es conmutativa.
es conmutativa.
Si un anillo cuenta con un elemento neutro para la segunda operación se llama anillo unitario. A dicho elemento se le suele llamar la unidad (1) para diferenciarlo del elemento neutro de la primera operación (usualmente el 0).
Definición sintética
Un anillo R es un conjunto con dos leyes de composición, llamadas adición y multiplicación, cumpliendo las condiciones siguientes:3
- R1. R es grupo abeliano para la adición; el elemento neutro en esta adición se nombra cero del anillo, y se denota usualmente 0;
- R2. R es un semigrupo para la multiplicación;
- R3. La multiplicación es distributiva (por los dos lados) respecto de la adición.
Ejemplos
- El conjunto de los enteros gaussianos H = {m+ni: m,n ∈ ℤ}, con la adición y múltiplicación usuales es un anillo unitario. Es un subanillo de los números complejos ℂ.
- El conjunto M de las matrices reales de orden 2 con la adición y multiplicación de matrices es un anillo no conmutativo.
- El conjunto Q(
 ) de los números reales: m+n
) de los números reales: m+n donde m, n ∈ ℚ (son racionales, con la adición y multiplicación, es un anillo unitario conmutativo.4
donde m, n ∈ ℚ (son racionales, con la adición y multiplicación, es un anillo unitario conmutativo.4 - El conjunto Z[6] de los enteros módulo 6; con la adición y multiplicación modular, es un anillo finito con divisores de 0.
- El conjunto F[x] de los polinomios con coeficientes en ℤ (conjunto de los enteros), con la adición y multiplicación, es un anillo unitario.
Elementos destacados en un anillo
- Elemento cero, denotado por
 , es el elemento neutro para la suma. Para este elemento se verifica lo siguiente:
, es el elemento neutro para la suma. Para este elemento se verifica lo siguiente:
- Sea A un anillo arbitrario.

| Demostración |
- Elemento unitario: si un elemento, que denotamos 1, cumple
 para todo elemento a del anillo, se llama elemento unitario. El elemento cero y el elemento unitario (caso de existir) sólo coinciden en el caso de que el anillo sea trivial:
para todo elemento a del anillo, se llama elemento unitario. El elemento cero y el elemento unitario (caso de existir) sólo coinciden en el caso de que el anillo sea trivial:
| Demostración |
- Inverso multiplicativo: en un anillo unitario, se pueden definir elementos inversos multiplicativos de la siguiente manera:
- el elemento
 es inverso multiplicativo por la izquierda (o sencillamente inverso por la izquierda) de
es inverso multiplicativo por la izquierda (o sencillamente inverso por la izquierda) de  si
si  .
. - Así mismo, el elemento
 es inverso multiplicativo por la derecha (o sencillamente inverso por la derecha) de
es inverso multiplicativo por la derecha (o sencillamente inverso por la derecha) de  si
si  .
.
- el elemento
- No todos los elementos tienen inverso, e incluso es posible que un elemento tenga inverso por la izquierda pero no por la derecha, o viceversa. Sin embargo, cuando un elemento a tiene elemento inverso por la izquierda y por la derecha, entonces ambos son iguales, y se denota simplemente como elemento inverso (
 ).
).
- Elemento inversible, elemento invertible o unidad: es todo aquel elemento que posee inverso multiplicativo.
- Divisor de cero: un elemento
 es divisor del cero por la izquierda, si existe algún
es divisor del cero por la izquierda, si existe algún 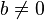 , tal que a·b=0. Lo es por la derecha si existe un
, tal que a·b=0. Lo es por la derecha si existe un  distinto de 0 tal que c·a=0. Se dirá que a es divisor del cero si lo es tanto por la derecha como por la izquierda.
distinto de 0 tal que c·a=0. Se dirá que a es divisor del cero si lo es tanto por la derecha como por la izquierda.
- Elemento regular: un elemento
 de un anillo es regular si no es divisor de cero. Todo elemento invertible es regular.
de un anillo es regular si no es divisor de cero. Todo elemento invertible es regular.
- Elemento idempotente: es cualquier elemento
 del anillo que al multiplicarse por sí mismo no varía, es decir, tal que
del anillo que al multiplicarse por sí mismo no varía, es decir, tal que  (o alternativamente
(o alternativamente  ). El cero es siempre idempotente en un anillo, y si el anillo es unitario, también el 1 es idempotente.
). El cero es siempre idempotente en un anillo, y si el anillo es unitario, también el 1 es idempotente.
- Elemento nilpotente (o nihilpotente): es cualquier elemento
 del anillo para el que existe un número natural
del anillo para el que existe un número natural  de forma que
de forma que  (donde
(donde  se define por recurrencia:
se define por recurrencia: 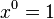 ,
,  ). El 0 es siempre un nilpotente de cualquier anillo. Todo elemento nilpotente es divisor de cero.
). El 0 es siempre un nilpotente de cualquier anillo. Todo elemento nilpotente es divisor de cero.
Algunos tipos importantes de anillos
- Anillo conmutativo: aquel en el que el producto es conmutativo, esto es, a·b=b·a para todos a y b (no debe confundirse con anillo abeliano). Como ejemplo: el conjunto
 de los números enteros pares con la suma y producto de enteros es un anillo conmutativo no unitario. En cambio; el conjunto
de los números enteros pares con la suma y producto de enteros es un anillo conmutativo no unitario. En cambio; el conjunto  de las matrices reales cuadradas de orden 2, con la suma y producto de matrices es un anillo unitario no conmutativo. 5
de las matrices reales cuadradas de orden 2, con la suma y producto de matrices es un anillo unitario no conmutativo. 5
- Anillo unitario: aquel que posee un elemento unitario y además, éste es distinto del neutro de la suma.
- Anillo de división: es el anillo en el cual todo elemento, a excepción del 0, tiene inverso.
- Anillo con leyes de simplificación: aquel en el que se cumplen las leyes de simplificación. Si un anillo no tiene divisores del cero, se cumplen las leyes de simplificación, y el recíproco también es cierto.
- Dominio de integridad: si un anillo no posee divisores del cero, es un dominio de integridad (a menudo se suele exigir que además se trate de anillos conmutativos y unitarios, pero esta exigencia no es aceptada por todos los autores).
- Cuerpo: se trata de un anillo de división conmutativo.
- Anillo abeliano: es un anillo en el que todo elemento idempotente pertenece al centro del anillo, es decir, todo elemento idempotente conmuta con cualquier elemento del anillo.
- Anillo euclideo6 o dominio euclídeo es un dominio de integridad R junto con una norma euclídea N. El anillo de los enteros, el de los enteros gaussianos y los anilllos de polinomios son ejemplos de dominios euclídeos.
Subsistemas notables
Subanillos
Un subanillo  de un anillo
de un anillo  =(A,+,·) es un subconjunto
=(A,+,·) es un subconjunto  que cumple que es cerrado para la suma y la multiplicación en el anillo, esto es, si
que cumple que es cerrado para la suma y la multiplicación en el anillo, esto es, si  , entonces
, entonces  y
y  . Si
. Si  (es decir, si el anillo es unitario), entonces se exigirá además que
(es decir, si el anillo es unitario), entonces se exigirá además que  . Nótese que en este caso, cuando el anillo es unitario, {0} no será subanillo de
. Nótese que en este caso, cuando el anillo es unitario, {0} no será subanillo de  , y sí lo será si
, y sí lo será si  no es unitario.
no es unitario.
 de un anillo
de un anillo  =(A,+,·) es un subconjunto
=(A,+,·) es un subconjunto  que cumple que es cerrado para la suma y la multiplicación en el anillo, esto es, si
que cumple que es cerrado para la suma y la multiplicación en el anillo, esto es, si  , entonces
, entonces  y
y  . Si
. Si  (es decir, si el anillo es unitario), entonces se exigirá además que
(es decir, si el anillo es unitario), entonces se exigirá además que  . Nótese que en este caso, cuando el anillo es unitario, {0} no será subanillo de
. Nótese que en este caso, cuando el anillo es unitario, {0} no será subanillo de  , y sí lo será si
, y sí lo será si  no es unitario.
no es unitario.
Un subanillo  es propio cuando no coincide con todo el anillo, es decir, si
es propio cuando no coincide con todo el anillo, es decir, si  .
.
 es propio cuando no coincide con todo el anillo, es decir, si
es propio cuando no coincide con todo el anillo, es decir, si  .
.
Resulta pues que un subanillo es un anillo dentro de otro anillo (para las mismas operaciones). En particular,  es un subgrupo de
es un subgrupo de  .
.
 es un subgrupo de
es un subgrupo de  .
.
Ejemplos:
-
- ℤ es un subanillo de ℚ; de la misma manera, ℚ es un subanillo de ℝ; y ℝ es un subanillo de ℂ.
- El conjunto de los números complejos algebraicos es un subanillo de ℂ.
Proposición
Un subconjunto K de un anillo A es subanillo de A si y solamente si
-
- K es subgrupo aditivo de A.
- De x, y elementos de K se colige que xy elemento de K. 7
Ideales
De mucho mayor interés en teoría de anillos son los ideales, puesto que no sólo son cerrados respecto de la multiplicación respecto de los elementos del ideal, sino también cuando un elemento del ideal se multiplica por cualquier elemento del anillo:
- Un subconjunto
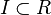 es ideal por la izquierda de un anillo (A,+,·) si
es ideal por la izquierda de un anillo (A,+,·) si  es subgrupo de
es subgrupo de  y dados cualesquiera
y dados cualesquiera 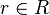 y
y 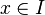 se tiene que
se tiene que  .
.
- Un subconjunto
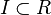 es ideal por la derecha de un anillo (A,+,·) si
es ideal por la derecha de un anillo (A,+,·) si  es subgrupo de
es subgrupo de  y dados cualesquiera
y dados cualesquiera 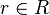 y
y 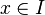 se tiene que
se tiene que  .
.
Cuando un subconjunto I es ideal por la derecha e ideal por la izquierda se dice que es un ideal bilátero, o simplemente ideal. La propiedad conmutativa asegura que en los anillos conmutativos todo ideal por la izquierda lo es también por la derecha, y todo ideal por la derecha es ideal por la izquierda, esto es, todos los ideales (por la izquierda o por la derecha) de un anillo conmutativo son ideales biláteros.
Un ideal no tiene por qué ser necesariamente un subanillo. Un ideal  se dice que es propio si es distinto de todo el anillo, esto es,
se dice que es propio si es distinto de todo el anillo, esto es,  .
.
 se dice que es propio si es distinto de todo el anillo, esto es,
se dice que es propio si es distinto de todo el anillo, esto es,  .
.Unidades
El conjunto de elementos invertibles de un anillo unitario  , llamados unidades de R, forma un grupo respecto de la multiplicación del anillo, que recibe el nombre de grupo de unidades de R, denotado
, llamados unidades de R, forma un grupo respecto de la multiplicación del anillo, que recibe el nombre de grupo de unidades de R, denotado  .
.
 , llamados unidades de R, forma un grupo respecto de la multiplicación del anillo, que recibe el nombre de grupo de unidades de R, denotado
, llamados unidades de R, forma un grupo respecto de la multiplicación del anillo, que recibe el nombre de grupo de unidades de R, denotado  .
.
Si  es ideal (por la izquierda, por la derecha o bilátero) propio de un anillo unitario
es ideal (por la izquierda, por la derecha o bilátero) propio de un anillo unitario  ,
,  es el grupo de unidades de R, entonces
es el grupo de unidades de R, entonces  , esto es, ningún ideal propio tiene elementos invertibles. En particular, ningún ideal (por la izquierda, por la derecha o bilátero) propio tiene por elemento al 1, lo que impide a los ideales ser subanillos de anillos unitarios.
, esto es, ningún ideal propio tiene elementos invertibles. En particular, ningún ideal (por la izquierda, por la derecha o bilátero) propio tiene por elemento al 1, lo que impide a los ideales ser subanillos de anillos unitarios.
 es ideal (por la izquierda, por la derecha o bilátero) propio de un anillo unitario
es ideal (por la izquierda, por la derecha o bilátero) propio de un anillo unitario  ,
,  es el grupo de unidades de R, entonces
es el grupo de unidades de R, entonces  , esto es, ningún ideal propio tiene elementos invertibles. En particular, ningún ideal (por la izquierda, por la derecha o bilátero) propio tiene por elemento al 1, lo que impide a los ideales ser subanillos de anillos unitarios.
, esto es, ningún ideal propio tiene elementos invertibles. En particular, ningún ideal (por la izquierda, por la derecha o bilátero) propio tiene por elemento al 1, lo que impide a los ideales ser subanillos de anillos unitarios.
Por ejemplo, las unidades del anillo de los enteros son 1 y -1 (isomorfo al grupo de dos elementos), y el grupo de unidades de las matrices cuadradas de orden n es elgrupo lineal general de orden n, que contiene a las matrices con determinante distinto de 0.
Centro
El centro de un anillo 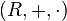 (denotado por
(denotado por  ) es el conjunto de elementos que conmutan para el producto, es decir
) es el conjunto de elementos que conmutan para el producto, es decir  . El centro de un anillo viene a ser como "la parte conmutativa del anillo". Nótese que siempre se tiene que
. El centro de un anillo viene a ser como "la parte conmutativa del anillo". Nótese que siempre se tiene que  . Los anillos conmutativos son aquellos que coinciden con su centro, i.e.,
. Los anillos conmutativos son aquellos que coinciden con su centro, i.e.,  .
.
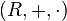 (denotado por
(denotado por  ) es el conjunto de elementos que conmutan para el producto, es decir
) es el conjunto de elementos que conmutan para el producto, es decir  . El centro de un anillo viene a ser como "la parte conmutativa del anillo". Nótese que siempre se tiene que
. El centro de un anillo viene a ser como "la parte conmutativa del anillo". Nótese que siempre se tiene que  . Los anillos conmutativos son aquellos que coinciden con su centro, i.e.,
. Los anillos conmutativos son aquellos que coinciden con su centro, i.e.,  .
.
Por ejemplo, el centro del anillo de las matrices cuadradas de orden n está constituido únicamente por las matrices escalares, aquellas que son iguales a la matriz identidad multiplicada por un escalar..
Consideremos un conjunto no vacío A, dotado de dos operaciones que convenimos en llamar suma y producto y en simbolizarlas como tales, aunque su naturaleza no sea la de las operaciones aritméticas usuales. Decimos que A es un anillo si respecto a la suma es un grupo conmutativo, respecto al producto es un semigrupo y el producto es distributivo respecto a la suma por ambos lados. Es decir, si para cualesquiera  es
es
existe un elemento  tal que
tal que
dado  siempre es posible hallar
siempre es posible hallar  tal que
tal que
y finalmente se cumple que
En cualquier anillo se precisa de la existencia de un cero (neutro aditivo). Por tanto, si tomamos un conjunto unitario  y definimos en él dos operaciones como
y definimos en él dos operaciones como  y
y  , tendremos trivialmente un anillo donde el único elemento (
, tendremos trivialmente un anillo donde el único elemento (  ) hace el papel del cero. Un ejemplo más interesante de anillo es el de los números enteros
) hace el papel del cero. Un ejemplo más interesante de anillo es el de los números enteros  con la suma y el producto aritméticos. Dentro de los anillos podemos aplicar las reglas de cálculo habituales. Por ejemplo, si A es un anillo y
con la suma y el producto aritméticos. Dentro de los anillos podemos aplicar las reglas de cálculo habituales. Por ejemplo, si A es un anillo y  son elementos de dicho anillo, tenemos
son elementos de dicho anillo, tenemos
Entendiendo que  representa al opuesto de
representa al opuesto de  . La demostración de esta última desigualdad resulta clarificadora pues nos muestra los procesos sutiles con los que hemos de trabajar en álgebra abstracta. En efecto, tomamos
. La demostración de esta última desigualdad resulta clarificadora pues nos muestra los procesos sutiles con los que hemos de trabajar en álgebra abstracta. En efecto, tomamos  y aplicamos la propiedad distributiva del producto respecto a la suma, la propiedad asociativa de la suma y la existencia de neutro aditivo, para obtener
y aplicamos la propiedad distributiva del producto respecto a la suma, la propiedad asociativa de la suma y la existencia de neutro aditivo, para obtener
Ahora sólo restaría sumar a ambos miembros el opuesto de  para llegar a la igualdad pedida
para llegar a la igualdad pedida
El lector observará el especial cuidado con el que se han de usar las propiedades establecidas en el anillo y, sobre todo, cómo ha de evitarse la tentación de “abreviar” inspirándose en la familiaridad de los símbolos.
Si un anillo A tiene elemento neutro para el producto se llama anillo unitario. Dicho neutro multiplicativo se suele notar como  , o simplemente 1 si no hay confusión. Para evitar trivialidades supondremos que en un anillo unitario hay al menos dos elementos diferentes: el uno y el cero. Cuando el producto es conmutativo decimos que el anillo es conmutativo. La teoría de anillos es una rama del álgebra de profundas y extensas implicaciones. En próximas entradas intentaremos mostrar algunas ideas más sobre esta estructura.
, o simplemente 1 si no hay confusión. Para evitar trivialidades supondremos que en un anillo unitario hay al menos dos elementos diferentes: el uno y el cero. Cuando el producto es conmutativo decimos que el anillo es conmutativo. La teoría de anillos es una rama del álgebra de profundas y extensas implicaciones. En próximas entradas intentaremos mostrar algunas ideas más sobre esta estructura.
No hay comentarios:
Publicar un comentario