Teoría de anillos
característica de un anillo  es definida como el entero positivo más pequeño
es definida como el entero positivo más pequeño  tal que
tal que  . Si no existe tal
. Si no existe tal  , se dice que la característica de
, se dice que la característica de  es 0.
es 0.
 es definida como el entero positivo más pequeño
es definida como el entero positivo más pequeño  tal que
tal que  . Si no existe tal
. Si no existe tal  , se dice que la característica de
, se dice que la característica de  es 0.
es 0.
De forma alternativa y equivalente, podemos definir la característica del anillo  como el único número natural
como el único número natural  tal que
tal que  contenga un subanillo isomorfo al anillo cociente
contenga un subanillo isomorfo al anillo cociente  .
.
 como el único número natural
como el único número natural  tal que
tal que  contenga un subanillo isomorfo al anillo cociente
contenga un subanillo isomorfo al anillo cociente  .
.El caso de anillos
 ,
,
entonces la característica de  divide la característica de
divide la característica de  . Esto puede a veces ser utilizado para excluir la posibilidad de cierto homomorfismo de anillos. El único anillo con característica 1 es el anillo trivial, el cual contiene un solo elemento 0=1. Si el anillo no trivial
. Esto puede a veces ser utilizado para excluir la posibilidad de cierto homomorfismo de anillos. El único anillo con característica 1 es el anillo trivial, el cual contiene un solo elemento 0=1. Si el anillo no trivial  no tienen ningún divisor de cero, entonces su característica es 0 ó primo. En particular, esto se aplica a todo cuerpo, a todo dominio de integridad y a todo anillo de división. Todo anillo de característica 0 es infinito.
no tienen ningún divisor de cero, entonces su característica es 0 ó primo. En particular, esto se aplica a todo cuerpo, a todo dominio de integridad y a todo anillo de división. Todo anillo de característica 0 es infinito.
 divide la característica de
divide la característica de  . Esto puede a veces ser utilizado para excluir la posibilidad de cierto homomorfismo de anillos. El único anillo con característica 1 es el anillo trivial, el cual contiene un solo elemento 0=1. Si el anillo no trivial
. Esto puede a veces ser utilizado para excluir la posibilidad de cierto homomorfismo de anillos. El único anillo con característica 1 es el anillo trivial, el cual contiene un solo elemento 0=1. Si el anillo no trivial  no tienen ningún divisor de cero, entonces su característica es 0 ó primo. En particular, esto se aplica a todo cuerpo, a todo dominio de integridad y a todo anillo de división. Todo anillo de característica 0 es infinito.
no tienen ningún divisor de cero, entonces su característica es 0 ó primo. En particular, esto se aplica a todo cuerpo, a todo dominio de integridad y a todo anillo de división. Todo anillo de característica 0 es infinito.
El anillo  de los enteros módulo
de los enteros módulo  tiene característica
tiene característica  . Si
. Si  es un subanillo de
es un subanillo de  , entonces
, entonces  y
y  tienen la misma característica. Por ejemplo, si
tienen la misma característica. Por ejemplo, si  es unpolinomio primo con coeficientes en el cuerpo
es unpolinomio primo con coeficientes en el cuerpo 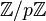 donde
donde  es primo, entonces el anillo factor
es primo, entonces el anillo factor ![(\mathbb{Z}/p\mathbb{Z})[X]/(q(X))](https://upload.wikimedia.org/math/7/6/2/762fbd30fa0a81665d2e2d47f1838036.png) es un cuerpo de característica
es un cuerpo de característica  . Como losnúmeros complejos contienen a los racionales, su característica es 0.
. Como losnúmeros complejos contienen a los racionales, su característica es 0.
 de los enteros módulo
de los enteros módulo  tiene característica
tiene característica  . Si
. Si  es un subanillo de
es un subanillo de  , entonces
, entonces  y
y  tienen la misma característica. Por ejemplo, si
tienen la misma característica. Por ejemplo, si  es unpolinomio primo con coeficientes en el cuerpo
es unpolinomio primo con coeficientes en el cuerpo 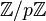 donde
donde  es primo, entonces el anillo factor
es primo, entonces el anillo factor ![(\mathbb{Z}/p\mathbb{Z})[X]/(q(X))](https://upload.wikimedia.org/math/7/6/2/762fbd30fa0a81665d2e2d47f1838036.png) es un cuerpo de característica
es un cuerpo de característica  . Como losnúmeros complejos contienen a los racionales, su característica es 0.
. Como losnúmeros complejos contienen a los racionales, su característica es 0.
Si un anillo conmutativo  tiene característica prima
tiene característica prima  , entonces se tiene que
, entonces se tiene que 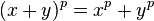 para todo elemento
para todo elemento  e
e  en
en  .
.
 tiene característica prima
tiene característica prima  , entonces se tiene que
, entonces se tiene que 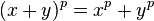 para todo elemento
para todo elemento  e
e  en
en  .
.
La aplicación
define un homomorfismo de anillos
 ,
,
dimensión de Krull de un anillo R al supremo de las longitudes de las cadenas de ideales primos ordenados por inclusión estricta.1 La dimensión de Krull puede ser infinita incluso en el caso de anillos noetherianos.
Un cuerpo tiene dimensión de Krull 0. Un dominio de ideales principales que no sea un cuerpo tiene dimensión 1. Un anillo de polinomios en n indeterminadas k[x1,...,xn] tiene dimensión de Krull n.
dominio presenta una seria dificultad. Por un lado designa originalmente a aquellos anillos conmutativos yunitarios en los que el elemento neutro para la suma y el elemento neutro para el producto no coinciden (esto es,  , es decir, cualquier anillo conmutativo y unitario que no sea el {0}).
, es decir, cualquier anillo conmutativo y unitario que no sea el {0}).
 , es decir, cualquier anillo conmutativo y unitario que no sea el {0}).
, es decir, cualquier anillo conmutativo y unitario que no sea el {0}).
Los dominios más interesantes eran, originalmente, los dominios de integridad, aquellos dominios que carecen de divisores de cero. Se conocían anillos no unitarios que carecían de divisores de cero (como el anillo  ), pero no se les daba el nombre de dominios de integridad. El problema vino cuando Mal'cev descubre un tipo de anillo unitario no conmutativo que no está isomorficamente incluido en un anillo de división de manera que cumpla la misma propiedad que el cuerpo de racionales de un dominio íntegro, y pasa a denominarse dominio de Mal'cev. Aparece ahora un tipo de anillo que no es conmutativo y que tiene la denominación de dominio.
), pero no se les daba el nombre de dominios de integridad. El problema vino cuando Mal'cev descubre un tipo de anillo unitario no conmutativo que no está isomorficamente incluido en un anillo de división de manera que cumpla la misma propiedad que el cuerpo de racionales de un dominio íntegro, y pasa a denominarse dominio de Mal'cev. Aparece ahora un tipo de anillo que no es conmutativo y que tiene la denominación de dominio.
 ), pero no se les daba el nombre de dominios de integridad. El problema vino cuando Mal'cev descubre un tipo de anillo unitario no conmutativo que no está isomorficamente incluido en un anillo de división de manera que cumpla la misma propiedad que el cuerpo de racionales de un dominio íntegro, y pasa a denominarse dominio de Mal'cev. Aparece ahora un tipo de anillo que no es conmutativo y que tiene la denominación de dominio.
), pero no se les daba el nombre de dominios de integridad. El problema vino cuando Mal'cev descubre un tipo de anillo unitario no conmutativo que no está isomorficamente incluido en un anillo de división de manera que cumpla la misma propiedad que el cuerpo de racionales de un dominio íntegro, y pasa a denominarse dominio de Mal'cev. Aparece ahora un tipo de anillo que no es conmutativo y que tiene la denominación de dominio.
En cualquier caso, al menos en el ámbito del Álgebra, la palabra dominio (a secas, sin añadiduras) sigue denominando a un anillo conmutativo unitario en el que  .
.
 .
.
dominio de factorización única (DFU) es un sistema algebraico, específicamente, es un dominio de integridad en el cual todo elemento se descompone de forma única (salvo producto por unidades) como producto de elementos primos (o elementos irreducibles). En los DFU se verifica que un elemento es primo si y sólo si esirreducible.
Ejemplos
Por ejemplo, el anillo de los números enteros es un caso particular de DFU, pero por lo general, no todo anillo es DFU; es fácil comprobar que en el anillo ![\mathbb{Z}[\sqrt{-5}]](https://upload.wikimedia.org/math/5/d/8/5d83b529eb7e9b1afe1219875d687fdf.png) ciertos elementos admiten más de una factorización.
ciertos elementos admiten más de una factorización.
![\mathbb{Z}[\sqrt{-5}]](https://upload.wikimedia.org/math/5/d/8/5d83b529eb7e9b1afe1219875d687fdf.png) ciertos elementos admiten más de una factorización.
ciertos elementos admiten más de una factorización.
Así,  , y los cuatro factores son irreducibles y no son unidades. Es un ejemplo de Anillo de factorización, pero no única. De hecho en este mismo anillo los cuatro factores no son ideales primos, pues los ideales que generan en
, y los cuatro factores son irreducibles y no son unidades. Es un ejemplo de Anillo de factorización, pero no única. De hecho en este mismo anillo los cuatro factores no son ideales primos, pues los ideales que generan en ![\mathbb{Z}[\sqrt{-5}]](https://upload.wikimedia.org/math/5/d/8/5d83b529eb7e9b1afe1219875d687fdf.png) no lo son:
no lo son:
 , y los cuatro factores son irreducibles y no son unidades. Es un ejemplo de Anillo de factorización, pero no única. De hecho en este mismo anillo los cuatro factores no son ideales primos, pues los ideales que generan en
, y los cuatro factores son irreducibles y no son unidades. Es un ejemplo de Anillo de factorización, pero no única. De hecho en este mismo anillo los cuatro factores no son ideales primos, pues los ideales que generan en ![\mathbb{Z}[\sqrt{-5}]](https://upload.wikimedia.org/math/5/d/8/5d83b529eb7e9b1afe1219875d687fdf.png) no lo son:
no lo son:
por lo tanto
Un resultado importante sobre este tipo de anillos es que si A es un DFU entonces A[X] también lo es.
Proposiciones
- Todo dominio de ideales principales es un dominio de factorización única.
- ℤ es un dominio de factorización única.
dominio de ideales principales (DIP) es un dominio de integridad en el que todo ideal es principal (está generado por un sólo elemento). Cualquier dominio de ideales principales es también un dominio de factorización única, pero no al revés; esto es, que un dominio entero sea DFU es una condición necesaria para sea un DIP.1 En estos dominios existe siempre el máximo común divisor y el mínimo común múltiplo, hecho que no ocurre en los dominios de integridad en general. El máximo común divisor de  y
y  en un DIP es el elemento
en un DIP es el elemento  del anillo tal que
del anillo tal que  .
.
 y
y  en un DIP es el elemento
en un DIP es el elemento  del anillo tal que
del anillo tal que  .
.Ejemplos
Ejemplos de dominio de ideales principales:
- El anillo
 de los números enteros.
de los números enteros. - El anillo de polinomios en una variable con coeficientes en el cuerpo
 ,
, ![\mathbb{K}[x]](https://upload.wikimedia.org/math/d/d/f/ddf3e61714833d45bad11d235837b772.png) .
. - El anillo de los enteros gaussianos,
![\mathbb{Z}[i]](https://upload.wikimedia.org/math/2/a/2/2a2fc748028420198e13c31eaadb6939.png) .
. - El anillo de los enteros de Eisenstein,
![\mathbb{Z}[\omega]](https://upload.wikimedia.org/math/1/4/7/147d28d2c4c6a0b2a4d039bd4a5cd041.png) donde
donde  es una raíz cúbica de la unidad en
es una raíz cúbica de la unidad en  .
.
Ejemplos de dominios íntegros que no son ideales principales:
- El anillo de los polinomios en una variable con coeficientes enteros,
![\mathbb{Z}[x]](https://upload.wikimedia.org/math/1/7/2/1720d8ed9c2582abffc3c0685c1ddb77.png) . Basta considerar el ideal generado por
. Basta considerar el ideal generado por  y
y  y observar que dicho ideal no puede ser generado por un solo elemento.
y observar que dicho ideal no puede ser generado por un solo elemento.
- Si
 es un cuerpo y
es un cuerpo y ![\mathbb{K}[x,y]](https://upload.wikimedia.org/math/1/d/6/1d6af1649d386557a0f0952d7799b9e6.png) es su anillo de polinomios en dos variables, entonces
es su anillo de polinomios en dos variables, entonces ![\mathbb{K}[x,y]](https://upload.wikimedia.org/math/1/d/6/1d6af1649d386557a0f0952d7799b9e6.png) no es dominio de ideales principales. Sea I el ideal generado por
no es dominio de ideales principales. Sea I el ideal generado por  e
e  es trivial ver que no puede generarse por un solo elemento. Además este dominio íntegro es un ejemplo de dominio de factorización única que no es dominio de ideales principales.
es trivial ver que no puede generarse por un solo elemento. Además este dominio íntegro es un ejemplo de dominio de factorización única que no es dominio de ideales principales.
Propiedades
Sea R un dominio íntegro, las siguientes proposiciones son equivalentes:
- R es un dominio de ideales principales.
- Cada ideal primo de R es principal.
- R es un dominio de factorización única y un dominio de Dedekind. (Existen DFU que no son DIP y Dominios de Dedekind que no son DIP, por ejemplo
![\mathbb{Z}[\sqrt{-5}]](https://upload.wikimedia.org/math/5/d/8/5d83b529eb7e9b1afe1219875d687fdf.png) es un dominio de Dedekind pero no un DIP).
es un dominio de Dedekind pero no un DIP). - Cada ideal finitamente generado de R es principal y se cumple la condición de cadena ascendente para ideales principales.
- R admite una norma Dedekind-Hasse.(Las normas Dedekind-Hasse son una generalización de las normas admitidas en los dominios euclideos).






No hay comentarios:
Publicar un comentario