Teoría de anillos
Los anillos ordenados son estructuras algebraicas propias de los conjuntos de números más comunes. Algunos ejemplos incluyen los enteros, los racionales y los reales. (Los racionales y los reales son, de hecho, cuerpos ordenados). Por otro lado, los números complejos no forman un anillo ordenado (o cuerpo).
Definiciones
- si
 y
y  , entonces
, entonces 
- si
 y
y  , entonces
, entonces 
Análogamente con los números ordinarios, decimos que un elemento c de un anillo ordenado es positivo si
 y negativo si
y negativo si  . El conjunto de los elementos positivos en un anillo
. El conjunto de los elementos positivos en un anillo  suele ser denotado por
suele ser denotado por  .
.
Si  es un elemento de un anillo ordenado
es un elemento de un anillo ordenado  , entonces el valor absoluto de
, entonces el valor absoluto de  , denotado por
, denotado por  , se define de la siguiente forma:
, se define de la siguiente forma:
 es un elemento de un anillo ordenado
es un elemento de un anillo ordenado  , entonces el valor absoluto de
, entonces el valor absoluto de  , denotado por
, denotado por  , se define de la siguiente forma:
, se define de la siguiente forma:Propiedades básicas
- Si
 y
y  , entonces
, entonces  Esta propiedad, a veces, se utiliza para definir anillos ordenados en lugar de la segunda propiedad en la definición de más arriba.
Esta propiedad, a veces, se utiliza para definir anillos ordenados en lugar de la segunda propiedad en la definición de más arriba. - Si
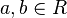 , entonces
, entonces 
- Un anillo ordenado no trivial es infinito.
- Si
 , entonces o
, entonces o  , o
, o  , o
, o  Esta propiedad se deriva del hecho que los anillos ordenados son abelianos, con orden total respecto la suma.
Esta propiedad se deriva del hecho que los anillos ordenados son abelianos, con orden total respecto la suma. - Un anillo ordenado
 no tiene divisores de cero si y solo si
no tiene divisores de cero si y solo si  es cerrado respecto el producto, es decir,
es cerrado respecto el producto, es decir,  es positivo si ambos
es positivo si ambos  y
y  son positivos.
son positivos.
Recordemos que un anillo  es un conjunto no vacío dotado de dos operaciones, que convenimos en notar como suma y producto y que verifican
es un conjunto no vacío dotado de dos operaciones, que convenimos en notar como suma y producto y que verifican
a)  es un grupo abeliano.
es un grupo abeliano.
b)  es un semigrupo
es un semigrupo
c) Para todos  es
es  y también
y también 
El neutro del grupo  se nota por 0. Si el semigrupo
se nota por 0. Si el semigrupo  es conmutativo decimos que el anillo es conmutativo y si
es conmutativo decimos que el anillo es conmutativo y si  tiene neutro decimos que el anillo es unitario y dicho neutro se nota por 1. Generalmente, prescindimos del símbolo “
tiene neutro decimos que el anillo es unitario y dicho neutro se nota por 1. Generalmente, prescindimos del símbolo “ ” para el producto y usamos la yuxtaposición. Esto es, escribimos
” para el producto y usamos la yuxtaposición. Esto es, escribimos  en lugar de
en lugar de  .
.
Si existe una relación  de orden (parcial o total) en un anillo conmutativo
de orden (parcial o total) en un anillo conmutativo  , decimos que dicha relación es compatible con las operaciones del anillo si y sólo si
, decimos que dicha relación es compatible con las operaciones del anillo si y sólo si
i)  es un grupo ordenado.
es un grupo ordenado.
ii) Para todos  , tales que
, tales que  ,
,  , es
, es  .
.
En lugar de hablar de órden compatible con la estructura de anillo decimos simplemente que el anillo es ordenado. Si  es un anillo ordenado podemos definir el cono positivo de la misma forma que hacíamos para los grupos ordenados:
es un anillo ordenado podemos definir el cono positivo de la misma forma que hacíamos para los grupos ordenados:
Es fácil probar que en un anillo ordenado, el cono positivo 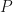 así definido, verifica:
así definido, verifica:
a)  .
.
b) .
.
c)  .
.
d)  .
.
Las propiedades a,b y c ya se demostraron en una entrada anterior y la propiedad d se deduce de la definición de anillo ordenado. En efecto, si  son elementos de
son elementos de 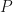 , entonces
, entonces  e
e  . Por tanto, aplicando ii) es
. Por tanto, aplicando ii) es  y esto significa que
y esto significa que , luego
, luego  .
.
Se puede probar que el cono positivo es unívoco para cada orden. Esto es, que podemos caracterizar a los anillos ordenados mediante dichos subconjuntos. En particular,
Teorema: Si  es un anillo conmutativo, son equivalentes:
es un anillo conmutativo, son equivalentes:
1. El anillo  está totalmente ordenado.
está totalmente ordenado.
2. Existe un subconjunto 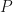 de
de  , que verifica:
, que verifica:  ,
,  ,
,  ,
,  y
y  .
.
Probaremos este y otros interesantes resultados en una entrada posterior.
anillo trivial es un anillo definido por un singulete, {r}. Las operaciones del anillo (× y +) son triviales:
Este anillo es claramente conmutativo. Su único elemento es el elemento identidad para ambas operaciones.
Un anillo R es trivial si y solo si 1 = 0, esta igualdad implica que para todo r de R, r = r × 1 = r × 0 = 0.
El anillo trivial también se le denomina anillo nulo, ya que {0} es un anillo con las operaciones estándares de la adición y la multiplicación.
anillo 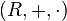 (no necesariamente conmutativo) es anillo unitario, o anillo unital, o anillo con unidad si existe un elemento en
(no necesariamente conmutativo) es anillo unitario, o anillo unital, o anillo con unidad si existe un elemento en  , diferente del neutro para la suma, que es elemento neutro para la operación producto ("·") del anillo, razón por la cual a dicho elemento se le denomina elemento unidad y se le representa por "1". A un anillo unitario se le suele representar como una cuaterna, en la que los primeros tres elementos representan al anillo (el conjunto, la operaciónrespecto de la cual es grupo abeliano, y la otra operación que es distributiva respecto de la primera) y el cuarto representa al elemento unidad. En nuestro caso sería
, diferente del neutro para la suma, que es elemento neutro para la operación producto ("·") del anillo, razón por la cual a dicho elemento se le denomina elemento unidad y se le representa por "1". A un anillo unitario se le suele representar como una cuaterna, en la que los primeros tres elementos representan al anillo (el conjunto, la operaciónrespecto de la cual es grupo abeliano, y la otra operación que es distributiva respecto de la primera) y el cuarto representa al elemento unidad. En nuestro caso sería  .
.
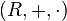 (no necesariamente conmutativo) es anillo unitario, o anillo unital, o anillo con unidad si existe un elemento en
(no necesariamente conmutativo) es anillo unitario, o anillo unital, o anillo con unidad si existe un elemento en  , diferente del neutro para la suma, que es elemento neutro para la operación producto ("·") del anillo, razón por la cual a dicho elemento se le denomina elemento unidad y se le representa por "1". A un anillo unitario se le suele representar como una cuaterna, en la que los primeros tres elementos representan al anillo (el conjunto, la operaciónrespecto de la cual es grupo abeliano, y la otra operación que es distributiva respecto de la primera) y el cuarto representa al elemento unidad. En nuestro caso sería
, diferente del neutro para la suma, que es elemento neutro para la operación producto ("·") del anillo, razón por la cual a dicho elemento se le denomina elemento unidad y se le representa por "1". A un anillo unitario se le suele representar como una cuaterna, en la que los primeros tres elementos representan al anillo (el conjunto, la operaciónrespecto de la cual es grupo abeliano, y la otra operación que es distributiva respecto de la primera) y el cuarto representa al elemento unidad. En nuestro caso sería  .
.Ejemplos
- Sea Z el conjunto de todos los números enteros: positivos, negativos y cero, con las operaciones usuales de adición y multiplicación. Z es un anillo conmutativo con elemento unitario, precisamente el 1.
- Sea T el conjunto de todos los enteros múltiplos de tres, con las operaciones de adición y multiplicación comunes. T es un anillo conmutativo, sin elemento unitario.
- Sea M[2] el conjunto de las matrices cuadradas de orden 2, bajo las operaciones de adición y multiplicación de matrices. M[2] es un anillo no conmutativo con elemento unitario , precisamente, la matriz identidad I.
Propiedades
En un anillo unitario existen:
- Elementos invertibles por la izquierda: un elemento
 del anillo es invertible por la izquierda (también se dice que x es una unidad por la izquierda del anillo, no confundir con el elemento unidad) si existe un elemento
del anillo es invertible por la izquierda (también se dice que x es una unidad por la izquierda del anillo, no confundir con el elemento unidad) si existe un elemento  de manera que
de manera que  .
. - Elementos invertibles por la derecha: un elemento
 del anillo es invertible por la derecha (también se dice que x es una unidad por la derecha del anillo, no confundir con el elemento unidad) si existe un elemento
del anillo es invertible por la derecha (también se dice que x es una unidad por la derecha del anillo, no confundir con el elemento unidad) si existe un elemento  de manera que
de manera que  .
. - Elementos invertibles: un elemento
 del anillo es invertible si es invertible (también se dice que x es una unidad del anillo, no confundir con el elemento unidad) por la derecha e invertible por la izquierda.
del anillo es invertible si es invertible (también se dice que x es una unidad del anillo, no confundir con el elemento unidad) por la derecha e invertible por la izquierda.
El elemento unidad de un anillo es invertible, luego es invertible por la izquierda e invertible por la derecha.Al conjunto de elementos invertibles de un anillo unitario R se le denota por U(R).
Si en un anillo unitario tomamos un ideal (por la izquierda, por la derecha o bilátero) y hay un elemento invertible que pertenece al ideal, entonces el ideal coincide con el anillo. En particular, en un anillo unitario, el elemento unidad 1 nunca pertenece a los ideales propios.
Una importante propiedad de los anillos unitarios es que en todo anillo unitario existen ideales maximales, es decir, ideales (biláteros) propios en el anillo de manera que no existe otro ideal (bilátero) propio que lo contenga.
Los anillos unitarios son los anillos sobre los que se construyen los módulos.
Homomorfismo de anillos unitarios
Un homomorfismo de anillos unitarios es una aplicación  entre los anillos unitarios
entre los anillos unitarios  y
y  tal que verifica que eshomomorfismo de anillos (esto es, si
tal que verifica que eshomomorfismo de anillos (esto es, si 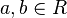 entonces
entonces  y
y  ) y que la imagen del elemento unidad es el elemento unidad (es decir,
) y que la imagen del elemento unidad es el elemento unidad (es decir,  ).
).
 entre los anillos unitarios
entre los anillos unitarios  y
y  tal que verifica que eshomomorfismo de anillos (esto es, si
tal que verifica que eshomomorfismo de anillos (esto es, si 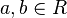 entonces
entonces  y
y  ) y que la imagen del elemento unidad es el elemento unidad (es decir,
) y que la imagen del elemento unidad es el elemento unidad (es decir,  ).
).
Si establecemos un homomorfismo de anillos  entre un anillo unitario
entre un anillo unitario  y un anillo
y un anillo  , entonces ha de ocurrir que
, entonces ha de ocurrir que  , con lo cual la imagen del elemento unidad ha de ser un idempotente.
, con lo cual la imagen del elemento unidad ha de ser un idempotente.
 entre un anillo unitario
entre un anillo unitario  y un anillo
y un anillo  , entonces ha de ocurrir que
, entonces ha de ocurrir que  , con lo cual la imagen del elemento unidad ha de ser un idempotente.
, con lo cual la imagen del elemento unidad ha de ser un idempotente. tal que
tal que
 es el
es el  es el
es el 

No hay comentarios:
Publicar un comentario