Teoría de anillos
dominio euclídeo (o anillo euclídeo) es un par  donde
donde  es un dominio de integridad y
es un dominio de integridad y  es una aplicación norma euclídea, es decir, una aplicación
es una aplicación norma euclídea, es decir, una aplicación  que cumple las siguientes dos condiciones:
que cumple las siguientes dos condiciones:
 donde
donde  es un dominio de integridad y
es un dominio de integridad y  es una aplicación norma euclídea, es decir, una aplicación
es una aplicación norma euclídea, es decir, una aplicación  que cumple las siguientes dos condiciones:
que cumple las siguientes dos condiciones: cualesquiera que sean
cualesquiera que sean  .
.
- Para cualesquiera
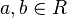 tales que
tales que  se cumple que existen
se cumple que existen  de manera que
de manera que  si
si  ha de ser
ha de ser  .
.
Es importante señalar que la definición es exactamente esa, aun cuando en algún caso particular pueda extenderse  a todo el conjunto R.
a todo el conjunto R.
 a todo el conjunto R.
a todo el conjunto R.Ejemplos
- Si tomamos el conjunto de los números enteros
 y como norma euclídea tomamos la aplicación valor absoluto
y como norma euclídea tomamos la aplicación valor absoluto  , tenemos un dominio euclídeo.
, tenemos un dominio euclídeo.
- Considerando el anillo de polinomios en una variable
![\mathbb{K}[x]](https://upload.wikimedia.org/math/d/d/f/ddf3e61714833d45bad11d235837b772.png) con coeficientes en el cuerpo
con coeficientes en el cuerpo  y como aplicación norma euclídea tomo el grado
y como aplicación norma euclídea tomo el grado  de cada polinomio, el resultado es un dominio euclídeo.
de cada polinomio, el resultado es un dominio euclídeo. - en el anillo de los enteros gaussianos α = a +bi, entonces se define norma de α, como N(α)= la suma de los cuadrados de a y b.
Ejemplos de norma euclídea
El valor absoluto es un ejemplo de norma euclídea en  , pues
, pues  para todo
para todo  y
y  de
de  con
con  , además de por lo indicado en el algoritmo de la división.
, además de por lo indicado en el algoritmo de la división.
 , pues
, pues  para todo
para todo  y
y  de
de  con
con  , además de por lo indicado en el algoritmo de la división.
, además de por lo indicado en el algoritmo de la división.
Además, en todo cuerpo  puede definirse una norma euclídea, tomándose ésta como la aplicación constante
puede definirse una norma euclídea, tomándose ésta como la aplicación constante  (el elemento neutro multiplicativo de
(el elemento neutro multiplicativo de  ), ya que, para cualesquiera elementos
), ya que, para cualesquiera elementos  y
y  de
de  , el elemento
, el elemento  y el elemento
y el elemento  aludidos en la definición de norma euclídea pueden tomarse como
aludidos en la definición de norma euclídea pueden tomarse como  y
y 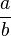 respectívamente, y así
respectívamente, y así  .
.
 puede definirse una norma euclídea, tomándose ésta como la aplicación constante
puede definirse una norma euclídea, tomándose ésta como la aplicación constante  (el elemento neutro multiplicativo de
(el elemento neutro multiplicativo de  ), ya que, para cualesquiera elementos
), ya que, para cualesquiera elementos  y
y  de
de  , el elemento
, el elemento  y el elemento
y el elemento  aludidos en la definición de norma euclídea pueden tomarse como
aludidos en la definición de norma euclídea pueden tomarse como  y
y 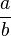 respectívamente, y así
respectívamente, y así  .
.
Un hecho menos evidente es que si  es un cuerpo, entonces el anillo de polinomios
es un cuerpo, entonces el anillo de polinomios ![\mathbb{K}[x]](https://upload.wikimedia.org/math/d/d/f/ddf3e61714833d45bad11d235837b772.png) tiene por norma euclídea la aplicación
tiene por norma euclídea la aplicación
 es un cuerpo, entonces el anillo de polinomios
es un cuerpo, entonces el anillo de polinomios ![\mathbb{K}[x]](https://upload.wikimedia.org/math/d/d/f/ddf3e61714833d45bad11d235837b772.png) tiene por norma euclídea la aplicación
tiene por norma euclídea la aplicación
que a cada polinomio no nulo de ![\mathbb{K}[x]](https://upload.wikimedia.org/math/d/d/f/ddf3e61714833d45bad11d235837b772.png) le asigna su grado.
le asigna su grado.
![\mathbb{K}[x]](https://upload.wikimedia.org/math/d/d/f/ddf3e61714833d45bad11d235837b772.png) le asigna su grado.
le asigna su grado.
Un dominio euclídeo E es un dominio de integridad en el cual cada elemento tiene asociado un entero concreto
tiene asociado un entero concreto  , y la función
, y la función  satisface las siguientes condiciones:
satisface las siguientes condiciones:
E1. Si divide a
divide a  , entonces
, entonces  .
.
E2. Para cada par de elementos de E, con
de E, con  , existen elementos
, existen elementos  y
y  de E tales que
de E tales que  con
con  .
.
E1. Si
E2. Para cada par de elementos
Esta definición tiene las siguientes consecuencias:
a. Si , entonces
, entonces  .
.
b. Si y
y  son asociados, entonces
son asociados, entonces  .
.
c. Si divide a
divide a  y
y  , entonces
, entonces  y
y  son asociados.
son asociados.
d. Si es una unidad, entonces
es una unidad, entonces  , y recíprocamente.
, y recíprocamente.
a. Si
b. Si
c. Si
d. Si
Teorema. Un dominio euclídeo es un dominio de factorización única.
Por el teorema anterior, basta verificar que un dominio euclídeo E cumple las condiciones UF1 y UF3. Zariski-Samuel demuestran por inducción respecto a que E cumple la condición UF1.
que E cumple la condición UF1.
Y para verificar que se cumple la condición UF3 demuestran el siguiente
Lema. Dos elementos tienen un máximo común divisor
tienen un máximo común divisor  y
y  es una combinación lineal de
es una combinación lineal de  y
y  , es decir,
, es decir,  .
.
Sea I el conjunto de todos los elementos de E que son combinaciones lineales de
de  y
y  . Entre los elementos de I diferentes de cero, elegimos un elemento
. Entre los elementos de I diferentes de cero, elegimos un elemento  para el que
para el que  es mínimo. Tenemos
es mínimo. Tenemos  , y por otro lado, por E2, podemos encontrar elementos
, y por otro lado, por E2, podemos encontrar elementos  y
y  en E tales que
en E tales que  . Tenemos entonces
. Tenemos entonces  y
y  . Por consiguiente,
. Por consiguiente,  , es decir,
, es decir,  divide a
divide a  . Similarmente se demuestra que
. Similarmente se demuestra que  divide a
divide a  , y por tanto
, y por tanto  es un divisor común de
es un divisor común de  y
y  . Además, puesto que
. Además, puesto que  es de la forma
es de la forma  , cada divisor comun de
, cada divisor comun de  y
y  es también un divisor de
es también un divisor de  . Por tanto
. Por tanto  es un máximo común divisor de
es un máximo común divisor de  y
y  . C.Q.D.
. C.Q.D.
Por el teorema anterior, basta verificar que un dominio euclídeo E cumple las condiciones UF1 y UF3. Zariski-Samuel demuestran por inducción respecto a
Y para verificar que se cumple la condición UF3 demuestran el siguiente
Lema. Dos elementos
Sea I el conjunto de todos los elementos de E que son combinaciones lineales
A partir del lema la verificación de UF3 es inmediata. Porque sea un elemento irreducible  de E que divide a un producto
de E que divide a un producto  , y asumamos que
, y asumamos que  no divide a
no divide a  . Entonces el máximo común divisor de
. Entonces el máximo común divisor de  y
y  es
es  , y por tanto, por el lema, podemos escribir
, y por tanto, por el lema, podemos escribir  . Por tanto
. Por tanto  , y puesto que
, y puesto que  , se sigue que
, se sigue que  .
.
dominio de integridad, dominio íntegro, anillo íntegro, dominio entero1 es un anillo 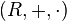 que carece de elementos divisores de cero por la izquierda y de elementos divisores de cero por la derecha (con lo cual carece de elementos divisores de cero).
que carece de elementos divisores de cero por la izquierda y de elementos divisores de cero por la derecha (con lo cual carece de elementos divisores de cero).
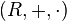 que carece de elementos divisores de cero por la izquierda y de elementos divisores de cero por la derecha (con lo cual carece de elementos divisores de cero).
que carece de elementos divisores de cero por la izquierda y de elementos divisores de cero por la derecha (con lo cual carece de elementos divisores de cero).
Un subanillo de un dominio de integridad es también un dominio de integridad.
En la literatura "antigua" se exige (a veces se sobreentiende) que el anillo es conmutativo y unitario, porque se ignoraba la existencia de anillos no conmutativos que no tuvieran divisores de cero (por la izquierda o por la derecha). Los dominios de Mal'cev son un tipo de anillos no conmutativos que carecen de elementos divisores de cero (ni por la izquierda ni por la derecha). Respecto a dominios íntegros no unitarios, el conjunto  es un subanillo no unitario del dominio de integridad
es un subanillo no unitario del dominio de integridad  . En este artículo, un dominio íntegro será siempre un anillo conmutativo y unitario (ya que así se entiende en la mayor parte de la literatura, señalándose los casos en que no se adopta estos criterios).
. En este artículo, un dominio íntegro será siempre un anillo conmutativo y unitario (ya que así se entiende en la mayor parte de la literatura, señalándose los casos en que no se adopta estos criterios).
 es un subanillo no unitario del dominio de integridad
es un subanillo no unitario del dominio de integridad  . En este artículo, un dominio íntegro será siempre un anillo conmutativo y unitario (ya que así se entiende en la mayor parte de la literatura, señalándose los casos en que no se adopta estos criterios).
. En este artículo, un dominio íntegro será siempre un anillo conmutativo y unitario (ya que así se entiende en la mayor parte de la literatura, señalándose los casos en que no se adopta estos criterios).
Todo cuerpo es dominio de integridad conmutativo y unitario. Más en general, todo anillo de división es dominio de integridad unitario.
Ejemplos


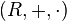
 2
2![(Z[i], +, \cdot)](https://upload.wikimedia.org/math/5/7/c/57ca14f0d3c8c7e26b0a51d92da76ad5.png) siendo Z[i] = {r+si/ r, s están en Z} es un dominio entero llamado anillo de los enteros de Gauss.
siendo Z[i] = {r+si/ r, s están en Z} es un dominio entero llamado anillo de los enteros de Gauss. siendo sus elementos los números reales
siendo sus elementos los números reales  con
con  números enteros
números enteros siendo sus elementos los números complejos
siendo sus elementos los números complejos  con
con  números enteros, i, unidad imaginaria.
números enteros, i, unidad imaginaria. siendo sus elementos los números reales
siendo sus elementos los números reales ![x = m+n\sqrt[3]{5} + p\sqrt[3]{25}](https://upload.wikimedia.org/math/4/2/8/428dc62e02e9b9d1bdcc15a04c8944e9.png) con
con  números enteros. 3
números enteros. 3
Cuerpo de cocientes de un dominio íntegro
Una de las propiedades más interesantes de un dominio de integridad es la de que existe «el menor cuerpo que lo contiene». De forma más precisa:
Sea  un dominio íntegro (conmutativo y unitario). Denotamos por
un dominio íntegro (conmutativo y unitario). Denotamos por 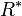 al conjunto
al conjunto  . Establecemos en el conjunto
. Establecemos en el conjunto  la relación
la relación  definida por
definida por  cuando y sólo cuando
cuando y sólo cuando  . Es sencillo comprobar que
. Es sencillo comprobar que  es una relación de equivalencia. Denotaremos por
es una relación de equivalencia. Denotaremos por  al conjunto cociente
al conjunto cociente  , y por
, y por 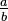 a la clase de equivalencia del par ordenado
a la clase de equivalencia del par ordenado  .
.
 un dominio íntegro (conmutativo y unitario). Denotamos por
un dominio íntegro (conmutativo y unitario). Denotamos por 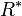 al conjunto
al conjunto  . Establecemos en el conjunto
. Establecemos en el conjunto  la relación
la relación  definida por
definida por  cuando y sólo cuando
cuando y sólo cuando  . Es sencillo comprobar que
. Es sencillo comprobar que  es una relación de equivalencia. Denotaremos por
es una relación de equivalencia. Denotaremos por  al conjunto cociente
al conjunto cociente  , y por
, y por 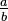 a la clase de equivalencia del par ordenado
a la clase de equivalencia del par ordenado  .
.Operaciones suma y producto en el cuerpo de cocientes
Suma
Se define la suma  de la siguiente manera:
de la siguiente manera:
 de la siguiente manera:
de la siguiente manera: ,
,
cualesquiera que sean  . Es sencillo comprobar que es operación interna, asociativa, conmutativa, que tiene elemento neutro
. Es sencillo comprobar que es operación interna, asociativa, conmutativa, que tiene elemento neutro  y que todo elemento
y que todo elemento  tiene por elemento simétrico (elemento opuesto) a
tiene por elemento simétrico (elemento opuesto) a  . Así,
. Así,  es un grupo abeliano.
es un grupo abeliano.
 . Es sencillo comprobar que es operación interna, asociativa, conmutativa, que tiene elemento neutro
. Es sencillo comprobar que es operación interna, asociativa, conmutativa, que tiene elemento neutro  y que todo elemento
y que todo elemento  tiene por elemento simétrico (elemento opuesto) a
tiene por elemento simétrico (elemento opuesto) a  . Así,
. Así,  es un grupo abeliano.
es un grupo abeliano.Producto
Se define la multiplicación  de la siguiente manera:
de la siguiente manera:
 de la siguiente manera:
de la siguiente manera: ,
,
cualesquiera que sean  . Es sencillo comprobar que es operación interna, asociativa, conmutativa, que tiene elemento neutro
. Es sencillo comprobar que es operación interna, asociativa, conmutativa, que tiene elemento neutro  y que todo elemento
y que todo elemento  tiene por elemento simétrico (elemento inverso) a
tiene por elemento simétrico (elemento inverso) a  . Así,
. Así,  es un grupo abeliano.
es un grupo abeliano.
 . Es sencillo comprobar que es operación interna, asociativa, conmutativa, que tiene elemento neutro
. Es sencillo comprobar que es operación interna, asociativa, conmutativa, que tiene elemento neutro  y que todo elemento
y que todo elemento  tiene por elemento simétrico (elemento inverso) a
tiene por elemento simétrico (elemento inverso) a  . Así,
. Así,  es un grupo abeliano.
es un grupo abeliano.Distributividad
Se demuestra sin dificultad que  es distributiva respecto de +. Esto hace que
es distributiva respecto de +. Esto hace que  quede dotado de estructura de cuerpo.
quede dotado de estructura de cuerpo.
 es distributiva respecto de +. Esto hace que
es distributiva respecto de +. Esto hace que  quede dotado de estructura de cuerpo.
quede dotado de estructura de cuerpo.Divisibilidad en un dominio íntegro (conmutativo y unitario) cualquiera
Quizás el aspecto más interesante que ofrecen los dominios íntegros es el de poder genralizar a ellos muchas de las propiedades sobre divisibilidad que conocemos en el anillo de los números enteros  .
.
 .
.
En adelante,  representarán elementos en el dominio íntegro
representarán elementos en el dominio íntegro  (i.e.
(i.e.  ).
).
 representarán elementos en el dominio íntegro
representarán elementos en el dominio íntegro  (i.e.
(i.e.  ).
).
Se dice que  y
y  son asociados si existe un
son asociados si existe un  de manera que
de manera que  . Se denota por
. Se denota por  .
.
 y
y  son asociados si existe un
son asociados si existe un  de manera que
de manera que  . Se denota por
. Se denota por  .
.
Se denota por  el conjunto formado por todos los divisores de la identidad, 1, llamados unidades del anillo.
el conjunto formado por todos los divisores de la identidad, 1, llamados unidades del anillo.
 el conjunto formado por todos los divisores de la identidad, 1, llamados unidades del anillo.
el conjunto formado por todos los divisores de la identidad, 1, llamados unidades del anillo.
Se dice que  divide a
divide a  si existe un
si existe un 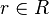 de manera que
de manera que  . Se denota por
. Se denota por  . Si
. Si  y
y  son asociados, entonces
son asociados, entonces  divide a
divide a  y
y  divide a
divide a  .
.
 divide a
divide a  si existe un
si existe un 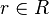 de manera que
de manera que  . Se denota por
. Se denota por  . Si
. Si  y
y  son asociados, entonces
son asociados, entonces  divide a
divide a  y
y  divide a
divide a  .
.
Se dice que un elemento  de un dominio íntegro
de un dominio íntegro  es un átomo o elemento irreducible (a veces se dice simplemente que es un irreducible) de
es un átomo o elemento irreducible (a veces se dice simplemente que es un irreducible) de  si
si 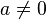 ,
,  , y si
, y si  entonces o bien es
entonces o bien es  o bien
o bien  (o los dos).
(o los dos).
 de un dominio íntegro
de un dominio íntegro  es un átomo o elemento irreducible (a veces se dice simplemente que es un irreducible) de
es un átomo o elemento irreducible (a veces se dice simplemente que es un irreducible) de  si
si 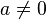 ,
,  , y si
, y si  entonces o bien es
entonces o bien es  o bien
o bien  (o los dos).
(o los dos).
Se dice que un elemento  de un dominio es un elemento primo (o simplemente primo) si el ideal generado por
de un dominio es un elemento primo (o simplemente primo) si el ideal generado por  es ideal primo de
es ideal primo de  .
.
 de un dominio es un elemento primo (o simplemente primo) si el ideal generado por
de un dominio es un elemento primo (o simplemente primo) si el ideal generado por  es ideal primo de
es ideal primo de  .
.
Lo cierto es que la notación es un poco confusa cuando nos referimos a los números enteros. En ese caso, el concepto de número primo corresponde con el de elemento irreducible (que además sea positivo), y tedríamos que el 0 y el 1 serían elementos primos de  , aunque no serían números primos.
, aunque no serían números primos.
 , aunque no serían números primos.
, aunque no serían números primos.
Si  es elemento primo del dominio íntegro
es elemento primo del dominio íntegro  ,
, 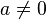 y
y  entonces
entonces  es irreducible.
es irreducible.
 es elemento primo del dominio íntegro
es elemento primo del dominio íntegro  ,
, 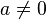 y
y  entonces
entonces  es irreducible.
es irreducible.Máximo común divisor y mínimo común múltiplo
Sean 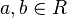 .
.
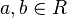 .
.- Un máximo común divisor de
 y
y  , (denotado por
, (denotado por  ) es, si existe, un elemento
) es, si existe, un elemento  de tal manera que
de tal manera que  ,
,  y si
y si  es tal que
es tal que  y
y  , entonces
, entonces  .
. - Un mínimo común múltiplo de
 y
y  , (denotado por
, (denotado por  ) es, si existe, un elemento
) es, si existe, un elemento  de tal manera que
de tal manera que  ,
,  y si
y si  es tal que
es tal que  y
y  , entonces
, entonces  .
.
Es de destacar que no se dice el máximo común denominador ni el mínimo común múltiplo, sino un máximo común divisor o un mínimo común múltiplo. Esto es debido a que, tal y como están definidos, un mismo par de elementos 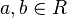 pueden tener más de un máximo común divisor y más de un mínimo común múltiplo. Por otra parte, en un dominio de integridad no siempre está asegurada la existencia del mínimo común múltiplo o del máximo común denominador de dos elementos cualesquiera.
pueden tener más de un máximo común divisor y más de un mínimo común múltiplo. Por otra parte, en un dominio de integridad no siempre está asegurada la existencia del mínimo común múltiplo o del máximo común denominador de dos elementos cualesquiera.
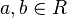 pueden tener más de un máximo común divisor y más de un mínimo común múltiplo. Por otra parte, en un dominio de integridad no siempre está asegurada la existencia del mínimo común múltiplo o del máximo común denominador de dos elementos cualesquiera.
pueden tener más de un máximo común divisor y más de un mínimo común múltiplo. Por otra parte, en un dominio de integridad no siempre está asegurada la existencia del mínimo común múltiplo o del máximo común denominador de dos elementos cualesquiera.
Dos elementos 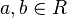 se dicen coprimos si existe
se dicen coprimos si existe  y además
y además  (es decir, 1 es
(es decir, 1 es  ).
).
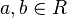 se dicen coprimos si existe
se dicen coprimos si existe  y además
y además  (es decir, 1 es
(es decir, 1 es  ).
).Propiedades
- Si
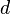 y
y  son
son  , entonces
, entonces  . Si
. Si  y
y  son
son  , entonces
, entonces  . Escribiremos entonces siempre
. Escribiremos entonces siempre  en lugar de
en lugar de  y
y  en lugar de
en lugar de  .
.  .
.- Si
 entonces
entonces  (es decir,
(es decir,  y
y  son coprimos).
son coprimos). - Si
 y
y  son coprimos (i.e.
son coprimos (i.e.  ), entonces, para cualquiera que sea
), entonces, para cualquiera que sea 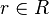 se cumple que
se cumple que  .
. - Si
 entonces
entonces  .
. - Si
 y
y  entonces
entonces  (en particular esto significa que si existe máximo común divisor de dos elementos, entonces existe su mínimo común múltiplo, y viceversa).
(en particular esto significa que si existe máximo común divisor de dos elementos, entonces existe su mínimo común múltiplo, y viceversa). - Si
 y
y  , entonces
, entonces  .
.
Estas son las principales afirmaciones que podemos decir sobre divisibilidad en dominios de integridad sin exigir más condiciones, como que el anillo R sea dominio de factorización única, dominio de ideales principales o que sea dominio euclídeo.
Elemento irreducible
En matemáticas, y más especialmente en teoría de anillos, una no-unidad en un dominio de integridad se dice que es irreducible si ésta no puede ser expresada como producto de dos no unidades. Equivalentemente, una no-unidad x es irreducible si x ≠ 0 y todo divisor dde x es un asociado de 1 o de x. Nótese que esta es la definición usual de número primo. Todo elemento primo es irreducible. El recíproco es verdadero también para dominios de factorización única. Un ideal generado por un elemento primo es un ideal primo. Sin embargo, no es cierto en general que un ideal generado por un elemento irreducible sea un ideal irreducible.1 Este es el caso en que Aes un dominio MCD (en particular un DFU).2
En lingüística, un elemento irreducible es aquel en el cual no se puede seguir analizando sintácticamente.
Sea  un dominio de integridad y
un dominio de integridad y  el conjunto de los elementos invertibles de
el conjunto de los elementos invertibles de  . Se dice que
. Se dice que  , siendo
, siendo  y
y  es un elemento irreducible en
es un elemento irreducible en  si cuando ocurre que
si cuando ocurre que  (con
(con  ) entonces también ha de ocurrir que
) entonces también ha de ocurrir que  o que
o que  .
.
 un dominio de integridad y
un dominio de integridad y  el conjunto de los elementos invertibles de
el conjunto de los elementos invertibles de  . Se dice que
. Se dice que  , siendo
, siendo  y
y  es un elemento irreducible en
es un elemento irreducible en  si cuando ocurre que
si cuando ocurre que  (con
(con  ) entonces también ha de ocurrir que
) entonces también ha de ocurrir que  o que
o que  .
.![\mathrm{grad}:\mathbb{K}[x] - \{0\} \longrightarrow\mathbb{N} \cup \{0\}](https://upload.wikimedia.org/math/8/b/d/8bdbb6bd791f5ca5a81f7948bed6dbbb.png)
No hay comentarios:
Publicar un comentario