Teoría de cuerpos

elemento trascendente de K, o simplemente trascendente sobre K, si no existe ningún polinomio g(x) con coeficientes en K tal que g(a)=0. Si existen elementos en L que cumplan las propiedades anteriores se llaman se denominanelementos algebraicos sobre K.

La extensión de cuerpos de estos elementos es C/Q, siendo C el cuerpo de los números complejos y Q el cuerpo de los números racionales.

Introducción

La teoría de cuerpos es una rama de la teoría de anillos, que a su vez es una rama del álgebra abstracta. Uno de las principales campos de estudio de la teoría de cuerpos es el de decidir si un polinomio cuyos coeficientes están en el cuerpo tiene sus raíces en el cuerpo (es decir, si al resolver la ecuación polinómica, las soluciones pertenecen o no al cuerpo).

Definición

Cuando un cuerpo está incluido en otro cuerpo puede ocurrir que los elementos del mayor sean raíces de polinomios con coeficientes en el menor — en cuyo caso se dice que los elementos son algebraicos — o que haya elementos que no son raíces de ninguno de esos polinomios. En este último caso se dice que dichos elementos sontrascendentes.

Construcción

(La siguiente información es de carácter técnico, y puede resultar ardua e incomprensible para el no iniciado en el álgebra abstracta, pero es esencial para comprender el desarrollo de esta rama de la matemática. Por desgracia no puede exponerse de una manera más llana sin perder rigor, lo que haría que dejara de ser útil.)

Sean dos cuerpos

(K,+,\cdot)

(L,+,\cdot)

de forma que

L

es extensión de

K

. Sea

\alpha \in L

. Si

\alpha \in K

, entonces

\alpha

es raíz del polinomio

p(x)= x - \alpha

, que esirreducible en

K[x]

(todo polinomio de grado 1 es irreducible en cualquier anillo de polinomios). Si

\alpha \in L \setminus K

, entonces realizamos la siguiente construcción:

Construimos el conjunto $K(\alpha):= \{\frac{f(\alpha)}{g(\alpha)}: f,g \in K[x]\}$ . Este conjunto es un cuerpo, es extensión de $K$ , es subcuerpo de $L$ , y de hecho es la menor extensión de $K$ que contiene a $\alpha$ . Se le denomina extensión generada por $\alpha$ sobre $K$ .

Construimos la aplicación $\beta: K[x] \longrightarrow K(\alpha)$ que a cada polinomio $p(x) \in K[x]$ le hace corresponder su evaluación en $\alpha$ , i.e., $\beta(p)=p(\alpha)$ . Esta aplicación es de hecho un homomorfirmo (no es isomorfismo en general) de anillos conmutativos y unitarios, y se denomina aplicación evaluación.

Ahora sólo pueden darse dos situaciones:

ker $(\beta) = \{0\}$ , luego $\beta$ es un monomorfismo. En ese caso, como $K \subset K[x]$ , es $\beta(a)=a$ para cada 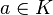$a \in K$ .

Demostración

$\ker(\beta) \neq \{0\}$ . Entonces se dice que $\alpha$ es un elemento algebraico.

En el primer caso (

\ker(\beta) = \{0\}

, o equivalentemente,

K(x) \cong K(\alpha)

) se dirá que el elemento

\alpha

es trascendente sobre

K

y que

K(\alpha)

es una extensión trascendente sobre

K

. En ese caso no existirá ningún polinomio con coeficientes en

K

que tenga por raíz a

\alpha

(es decir, si

p \in K[x]

, entonces

p(\alpha) \neq 0

endomorfismo de Frobenius es un endomorfismo de anillos de característica un número primo. En ciertos contextos es un automorfismo, pero este hecho no es cierto en general.

Sea R un anillo conmutativo de característica un número positivo y primo p (la característica es siempre un número primo cuando R es un dominio de integridad, por ejemplo). El endomorfismo de Frobenius F se define como

F(r)=r^p

para todo r de R. Se puede ver como esta aplicación respecta la multiplicación de elementos de R: F(rs)=(rs)^p = r^ps^p así como la suma en R. La expresión (r + s)^p puede ser desarrollada usando el teorema del binomio, y como p es primo, los coeficientes de todos los términos excepto r^p y s^p son divisibles por p, la característica, por lo que son iguales a cero. Finalmente vemos que claramente F(1)=1, por lo que acabamos de demostrar que F es un homomorfismo de anillos.

En general, F no es un automorfismo. Por ejemplo, sea K el cuerpo F_p(t), es decir, un cuerpo finito con p elementos junto con un solo elemento trascendente. Podemos afirmar que la imagen de F no contiene t. Demostraremos este hecho por contradicción: Suponemos que existe un elemento de K cuya imagen al aplicarle F es t. Dicho elemento es una función racional q(t)/r(t) cuya potencia p-esima (q(t)/r(t))^p es igual a t. Esto implica que p(deg q - deg r) = 1, lo cual es imposible. Por lo que F no esexhaustiva (suprayectiva) y por tanto no es un automorfismo. Incluso es posible que F no sea inyectiva. Esto ocurre si y solo si R tiene un elemento nilpotente de orden inferior o igual a p.

Puntos fijos en el endomorfismo de Frobenius

Iterando la aplicación de Frobenius obtenemos una secuencia de elementos de R:

x, x^p, x^{p^2}, x^{p^3}, \ldots

Aplicando iterativamente e veces F a un anillo que contenga un cuerpo K de p^e elementos se obtiene un conjunto de puntos fijos igual a K, similar al ejemplo anterior. Los iterados de la aplicación de Frobenius se usan para definir la clausura de Frobenius y la clausura estricta de un ideal.

Frobenius para cuerpos finitos

Sea F_q el cuerpo finito de q elementos, donde q=p^e.

F deja fijo F_p con dicho argumento. Si q=2, entonces F², la segunda iteración de Frobenius, deja fijos p² elementos, por lo que deja fijo

{\bold F}_{p^2}

En general, F^e deja fijo

{\bold F}_{p^e}

Además, F genera el Grupo de Galois de cualquier extensión de cuerpos finitos.

Endomorfismo de Frobenius

En álgebra conmutativa y teoría de cuerpos, que son ramas de las matemáticas, el endomorfismo de Frobenius es un endomorfismo de anillos decaracterística un número primo. En ciertos contextos es un automorfismo, pero este hecho no es cierto en general.
Sea R un anillo conmutativo de característica un número positivo y primer p (la característica es siempre un número primo cuando R es un dominio deintegridad, por ejemplo). El endomorfismo de Frobenius F se define como

F (r) = r ^p

para todo r deR. Se puede ver cómo esta aplicación respeta la multiplicación de elementos deR: F (rs) = (rs) ^p = r ^p s ^p así como la suma en R. La expresión (r + s) ^p puede ser desarrollada usando el teorema del binomio, y como p es primo, los coeficientes de todos los términos excepto r ^p y s ^p son divisibles por p, la característica, por lo que son iguales a cero. Finalmente vemos que claramente F (1) = 1, por lo que acabamos de demostrar que F es un homomorfismo de anillos.
En general, F no es un automorfismo. Por ejemplo, sea K el cuerpo F _p (t), es decir, un cuerpo finito con p elementos junto con un solo elementotrascendente. Podemos afirmar que la imagen de F no contiene t. Demostraremos este hecho por contradicción: Supongamos que existe un elemento deK la imagen de la que al aplicarle F es t. Dicho elemento es una función racional q (t) / r (t) que su potencia p -ésima (q (t) / r (t)) ^p es igual a t. Esto implica que p (deg q - deg r) = 1, lo cual es imposible. Por que F no es exhaustiva (suprayectiva) y por tanto no es un automorfismo. Incluso es posible que F no sea inyectiva. Esto ocurre si y solo si R tiene un elemento nilpotente de orden inferior o igual a p.

Puntos fijos en el endomorfismo de Frobenius

Sea R un dominio de integridad. La aplicación de Frobenius deja fijos todos los elementos deR que satisfacen la ecuación x ^p = x. Estas son todas las raíces de la ecuación x ^p - x, y como esta ecuación tiene grado p, hay como muchop raíces. Estas son exactamente los elementos 0, 1, 2, ..., p - 1, así que el conjunto de puntos fijos de F definen un cuerpo primero.
Iterando la aplicación de Frobenius obtenemos una secuencia de elementos de R: .3}, \ ldots "src =" ../../../../ math / d / 3 / f / d3f90b10086fc5bf24d409a0455054a7.png "/ \>

escalar a los números reales, constantes o complejos que sirven para describir un fenómeno físico (o de otro tipo) con magnitud, pero sin la característicavectorial de dirección. Formalmente es un tensor de rango cero.

En términos matemáticos, se llama escalar a los elementos de un cuerpo (en algunos casos también a los elementos de un anillo), generalmente números, y en particular se usa cuando se quiere distinguirlos claramente de los vectores en el álgebra lineal y en cualquier rama que use módulos o espacios vectoriales.

Definición y propiedades

Escalares de espacios vectoriales

Un espacio vectorial se define como un conjunto de vectores, un conjunto de escalares, y una operación de producto escalar que lleva a que un escalar k y un vector v dé un nuevo vector kv. Por ejemplo, en un espacio de coordenadas , el producto escalar k(v₁,v₂,...,v_n) da (kv₁,kv₂,...,kv_n). En una función (lineal) en el espacio, kf es la función x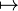

\mapsto

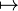k(f(x)).

Los escalares se pueden tomar de cualquier campo, incluyendo los números racionales, algebraicos, reales y complejos, así como campos finitos.

Escalares como componentes vectoriales

De acuerdo con el teorema fundamental del álgebra lineal, cada espacio vectorial tiene una base. Se deduce que cada espacio vectorial sobre un campo escalar K esisomorfo a un espacio vectorial de coordenadas, donde las coordenadas son elementos de K. Por ejemplo, cada espacio vectorial real de dimensión n es isomorfo al espacio real de n dimensiones R_n.

Producto escalar

El espacio de producto escalar es un espacio vectorial V con una operación adicional de producto escalar (o producto interno) que permite a dos vectores producir un número o escalar. Este escalar es un elemento del cuerpo de escalares sobre el que se define el espacio vectorial V

Como el producto interno de un vector consigo mismo debe ser no negativo, un espacio de producto escalar solo se puede definir sobre campos que
soportan la noción de signo (lo cuál excluye a los cuerpos finitos o los cuerpos sobre
los complejos, aunque en este último
caso se puede definir como producto interno una forma hermítica definida positiva, y el problema desaparece).

La existencia del producto escalar, hace posible introducir la noción geométrica de ángulo entre dos vectores, y permite formalizar que dos vectores sean ortogonales. La mayoría de espacios de productos escalares se pueden considerar un espacio vectorial normado de una manera natural.

Escalares en espacios vectoriales normados

Alternativamente, un espacio vectorial V puede dotarse de una función norma que asigna a cada vector v de V un escalar ||v||. Por definición, multiplicando v por un escalar k su norma queda multiplicada por |k|. Si ||v|| se interpreta como la "longitud" de v, esta operación puede describrse como un cambio de escala de la longitud de v mediante el factor k. Un espacio vectorial dotado de una nomra se llama espacio vectorial normado (o espacio lineal normado).

La norma se define usualmente como un elemento de V del campo de escalares K. Además si V tiene dimensión 2 o más el campo K debe ser cerrado bajo la extracción de raíces cuadradas. Esto hace que un espacio vectorial sobre Q no puede dotarse de una norma, ya que la raíz cuadrada de ciertos números racionales no es un número racional.

El producto escalar de dos vectores es un número real que resulta al multiplicar el producto de sus módulos por el coseno del ángulo que forman.