Teoría de anillos
elemento de un anillo es primo si satisface una condición similar a la establecida por el lema de Euclides.
|
O condensando: Un elemento k no nulo y no invertible de un anillo R se llama primo, si cada vez que k divide al producto de dos elementos de R, también divide uno de sus factores. Se ve que si a es primo, entonces todo asociado de a es primo.1
Esto es equivalente a la condición que el ideal principal generado por el elemento p sea un ideal primo distinto de cero.
Relación con elementos irreducibles
La definición usual de número primo estable que es aquél que sólo tiene por factores a sí mismo y a la unidad. Esta condición se generaliza en teoría de anillos en el concepto de elemento irreducible:
|
Un elemento no nulo y no invertible de un anillo se llama irreducible si sus únicos divisores son los elementos invertibles del anillo y sus propios asociados.2 Ejemplo 3 es irreducible en Z, ya que sus únicos divisores son 1, -1, 3, -3.
Sin embargo, en un dominio de factorización única ambos conceptos son equivalentes (un elemento primo es irreducible y viceversa). Sin embargo, dicha relación no es válida en general.
En un dominio principal, todo elemento irreducible es primo.
En Z un elemento es primo s.s.s. es irreducible.
El anillo de los enteros es un dominio de factorización única. De ahí sigue el TFA.
esquema es un tipo de estructura abstracta que aúna estructuras de tipo geométrico, de tipo algebraico y de teoría de números. La noción de esquema se remonta a los años 1960, cuando Alexander Grothendieck formuló el concepto generalizando la noción de variedad algebraica.
Muchos matemáticos consideran que los esquemas son objetos básicos de estudio de la geometría algebraica moderna. Técnicamente, un esquema es un espacio topológico provisto de anillos conmutativos para cada uno de sus abiertos.
Definición
Un esquema es un espacio localmente anillado (X, OX ) localmente isomorfo a un esquema afín, es decir para el que existe un recubrimiento por abiertos Ui tal que (Ui,OX|Ui ) es isomorfo –como espacio anillado– a (Spec (A), Â), donde A es un anillo conmutativo y  es su haz de localizaciones.
esquema afín a todo espacio anillado (Spec'A, à ) donde A es un anillo y à es su haz de localizaciones homogéneas. Es una noción introducida por Alexander Grothendieck en la década de los 60. Los esquemas afines hacen el papel en geometría algebraica de los abiertos coordenados en geometría diferencial y son por tanto un análogo al caso local en ella.
Haz de localizaciones homogéneas
Todo anillo A da un prehaz sobre su espectro Spec_A que en cada abierto básico "Ua" vale el localizado "Aa". El haz de anillos asociado "Â" se llama haz de localizaciones homogéneas de A.
homomorfismo de anillos es una aplicación entre anillos que conserva las estructuras de ambos como anillos.
En todo el artículo 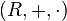 y
y  son anillos.
son anillos.
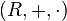 y
y  son anillos.
son anillos.Definiciones
Dado que existen distintos tipos de anillos, hay que particularizar la definición.
Caso general
Se dirá que la aplicación 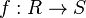 es un homomorfismo de anillos si se cumplen las siguientes dos condiciones:
es un homomorfismo de anillos si se cumplen las siguientes dos condiciones:
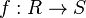 es un homomorfismo de anillos si se cumplen las siguientes dos condiciones:
es un homomorfismo de anillos si se cumplen las siguientes dos condiciones: , cualesquiera que sean
, cualesquiera que sean 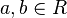 .
. , cualesquiera que sean
, cualesquiera que sean 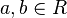 .
.
La primera condición nos dice que  es en particular un homomorfismo de grupos entre los grupos abelianos
es en particular un homomorfismo de grupos entre los grupos abelianos  y
y  . Con esta definición se ve que la imagende
. Con esta definición se ve que la imagende  ,
,  , es un subanillo de
, es un subanillo de  .
.
 es en particular un homomorfismo de grupos entre los grupos abelianos
es en particular un homomorfismo de grupos entre los grupos abelianos  y
y  . Con esta definición se ve que la imagende
. Con esta definición se ve que la imagende  ,
,  , es un subanillo de
, es un subanillo de  .
.
Se define el núcleo de f como el conjunto  , es decir,
, es decir,  . El núcleo de cualquier homomorfismo es un ideal(bilátero).
. El núcleo de cualquier homomorfismo es un ideal(bilátero).
 , es decir,
, es decir,  . El núcleo de cualquier homomorfismo es un ideal(bilátero).
. El núcleo de cualquier homomorfismo es un ideal(bilátero).Anillos unitarios
Si  y
y  son anillos unitarios (cuyos elementos unidades son respectivamente
son anillos unitarios (cuyos elementos unidades son respectivamente  y
y  ), entonces la aplicación
), entonces la aplicación  se dirá que es un homomorfismo de anillos unitarios si es un homomorfismo de anillos y además se cumple que
se dirá que es un homomorfismo de anillos unitarios si es un homomorfismo de anillos y además se cumple que  .
.
 y
y  son anillos unitarios (cuyos elementos unidades son respectivamente
son anillos unitarios (cuyos elementos unidades son respectivamente  y
y  ), entonces la aplicación
), entonces la aplicación  se dirá que es un homomorfismo de anillos unitarios si es un homomorfismo de anillos y además se cumple que
se dirá que es un homomorfismo de anillos unitarios si es un homomorfismo de anillos y además se cumple que  .
.
El resto de conceptos definidos en el apartado Caso general son válidos sin modificar nada para anillos unitarios.
Propiedades
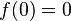 . En efecto,
. En efecto,  , luego
, luego 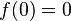 .
.
- Si R' es subanillo de R, entonces
 es subanillo de S.
es subanillo de S.
- Si S' es subanillo de S, entonces
 es subanillo de R.
es subanillo de R.
- Sean R y S dos anillos y ƒ un homomorfismo de R en S, entonces el núcleo de ƒ es un ideal bilátero.
- Sean R y S dos anillos y ƒ un homomorfismo de anillos de R en S. Entonces:
- si J es un ideal bilátero de S,
 es un ideal bilátero de R. Si, además, J es un ideal primo de S, entonces
es un ideal bilátero de R. Si, además, J es un ideal primo de S, entonces  es un ideal primo de R.
es un ideal primo de R.
- si J es un ideal bilátero de S,
- Si I es ideal por la izquierda de S, entonces
 es ideal por la izquierda de R.
es ideal por la izquierda de R.
- Si I es ideal por la izquierda de S, entonces
- Si I es ideal por la derecha de S, entonces
 es ideal por la derecha de R.
es ideal por la derecha de R.
- Si I es ideal por la derecha de S, entonces
- Sea R un anillo e I un ideal bilátero de R, entonces la aplicación canónica de R en el anillo cociente R/I es un homomorfismo suprayectivo.
- Si ƒ es homomorfismo exhaustivo e I es ideal por la izquierda de R, entonces
 es ideal por la izquierda de R.
es ideal por la izquierda de R.
- Si ƒ es homomorfismo exhaustivo e I es ideal por la izquierda de R, entonces
- Si ƒ es homomorfismo exhaustivo e I es ideal por la derecha de R, entonces
 es ideal por la derecha de R.
es ideal por la derecha de R.
- Si ƒ es homomorfismo exhaustivo e I es ideal por la derecha de R, entonces
- Si ƒ es homomorfismo exhaustivo e I es ideal de R, entonces
 es ideal de R.
es ideal de R.
- Si ƒ es homomorfismo exhaustivo e I es ideal de R, entonces
- Sean R y S dos anillos, y ƒ un homomorfismo de anillos de R en S. Usemos la notación s para la aplicación canónica de R en el anillo cociente R/I e i para el homomorfismo de ƒ(R) en S que a b asocia b. Entonces, i es un homomorfismo inyectivo, s es suprayectivo y existe una biyección b tal que:

Tipos de homomorfismos de anillos
Se dice que  es un monomorfismo si es una aplicación inyectiva, es decir,
es un monomorfismo si es una aplicación inyectiva, es decir,  implica que
implica que  , cualesquiera que sean
, cualesquiera que sean 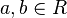 . Esto es equivalente a decir que
. Esto es equivalente a decir que  .
.
 es un monomorfismo si es una aplicación inyectiva, es decir,
es un monomorfismo si es una aplicación inyectiva, es decir,  implica que
implica que  , cualesquiera que sean
, cualesquiera que sean 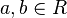 . Esto es equivalente a decir que
. Esto es equivalente a decir que  .
.
Se dice que  es un epimorfismo si es una aplicación sobreyectiva, es decir,
es un epimorfismo si es una aplicación sobreyectiva, es decir,  . No obstante, muchos autores prefieren no utilizar esta denominación, y hablar sólo de homomorfismos sobreyectivos (u homomorfismos exhaustivos). La razón es que el término epimorfismo tiene un significado más general en Teoría de Categorías. Desde este punto de vista (categórico), un epimorfismo de anillos no es necesariamente una aplicación sobreyectiva, aunque todos los homomorfismos de anillos sobreyectivos sí resultan ser epimorfismos.
. No obstante, muchos autores prefieren no utilizar esta denominación, y hablar sólo de homomorfismos sobreyectivos (u homomorfismos exhaustivos). La razón es que el término epimorfismo tiene un significado más general en Teoría de Categorías. Desde este punto de vista (categórico), un epimorfismo de anillos no es necesariamente una aplicación sobreyectiva, aunque todos los homomorfismos de anillos sobreyectivos sí resultan ser epimorfismos.
 es un epimorfismo si es una aplicación sobreyectiva, es decir,
es un epimorfismo si es una aplicación sobreyectiva, es decir,  . No obstante, muchos autores prefieren no utilizar esta denominación, y hablar sólo de homomorfismos sobreyectivos (u homomorfismos exhaustivos). La razón es que el término epimorfismo tiene un significado más general en Teoría de Categorías. Desde este punto de vista (categórico), un epimorfismo de anillos no es necesariamente una aplicación sobreyectiva, aunque todos los homomorfismos de anillos sobreyectivos sí resultan ser epimorfismos.
. No obstante, muchos autores prefieren no utilizar esta denominación, y hablar sólo de homomorfismos sobreyectivos (u homomorfismos exhaustivos). La razón es que el término epimorfismo tiene un significado más general en Teoría de Categorías. Desde este punto de vista (categórico), un epimorfismo de anillos no es necesariamente una aplicación sobreyectiva, aunque todos los homomorfismos de anillos sobreyectivos sí resultan ser epimorfismos.
Se dice que  es un isomorfismo si existe el homomorfismo inverso
es un isomorfismo si existe el homomorfismo inverso  de manera que
de manera que  y
y  . Esto ocurre si y sólo
. Esto ocurre si y sólo  si es una aplicación biyectiva, es decir,
si es una aplicación biyectiva, es decir,  , es a la vez monomorfismo y homomorfismo exhaustivo.
, es a la vez monomorfismo y homomorfismo exhaustivo.
 es un isomorfismo si existe el homomorfismo inverso
es un isomorfismo si existe el homomorfismo inverso  de manera que
de manera que  y
y  . Esto ocurre si y sólo
. Esto ocurre si y sólo  si es una aplicación biyectiva, es decir,
si es una aplicación biyectiva, es decir,  , es a la vez monomorfismo y homomorfismo exhaustivo.
, es a la vez monomorfismo y homomorfismo exhaustivo.
No hay comentarios:
Publicar un comentario