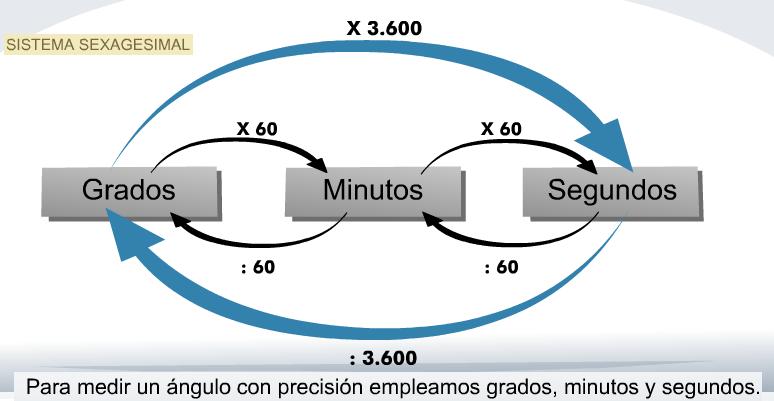
Unidades de ángulo
El minuto terrestre es una unidad de ángulo. Equivale al ángulo que gira la Tierra en un minuto. Esta unidad es utilizada en Astronomíay vale 15 minutos sexagesimales o un cuarto de grado sexagesimal.
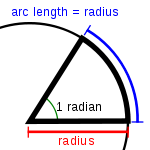
radián es la unidad de ángulo plano en el Sistema Internacional de Unidades. Representa el ángulo central en una circunferencia y abarca un arco cuya longitud es igual a la del radio. Su símbolo es rad. Hasta 1995 tuvo la categoría de unidad suplementaria en el Sistema Internacional de Unidades, junto con el estereorradián. A partir de ese año, y hasta el momento presente, ambas unidades figuran en la categoría de unidades derivadas.
Esta unidad se utiliza primordialmente en física, cálculo infinitesimal, trigonometría, goniometría, etc.
Definición
El ángulo formado por dos radios de una circunferencia, medido en radianes, es igual a la longitud del arco que delimitan los radios dividida entre el radio; es decir, θ = s/r, donde θ es ángulo, s es la longitud de arco, y r es el radio. Por tanto, el ángulo completo,  , que subtiende una circunferencia de radio r, medido en radianes, es:
, que subtiende una circunferencia de radio r, medido en radianes, es:
 , que subtiende una circunferencia de radio r, medido en radianes, es:
, que subtiende una circunferencia de radio r, medido en radianes, es:Utilidad
El radián es una unidad sumamente útil para medir ángulos, puesto que simplifica los cálculos, ya que los más comunes se expresan mediante sencillos múltiplos o divisores de π.
Análisis dimensional
El radián es la unidad natural en la medida de los ángulos. Por ejemplo, la función seno de un ángulo x expresado en radianes cumple:
donde x se expresa en radianes.
Equivalencias
- La equivalencia entre grados sexagesimales y radianes es: π rad = 180°. Por tanto
1 radián = 57.29577951... grados sexagesimales y
1 grado sexagesimal = 0.01745329252... radianes.
- La equivalencia entre grados centesimales y radianes es: π rad = 200g
La tabla muestra la conversión de los ángulos más comunes.
| Grados | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
| Radianes | 0 | π/6 | π/4 | π/3 | π/2 | 2π/3 | 3π/4 | 5π/6 | π | 7π/6 | 5π/4 | 4π/3 | 3π/2 | 5π/3 | 7π/4 | 11π/6 | 2π |
Otras unidades de medida de ángulos convencionales son el grado sexagesimal, el grado centesimal y, en astronomía, la hora.
- El Radián tiene una unidad derivada llamada radián por segundo (rad/s) (velocidad angular). Esta tiene una equivalencia con las rpm. Las equivalencias se pueden calcular fácilmente con la ecuación que sigue:
- De rpm a π rad/s
 que con la ecuación simplificada:
que con la ecuación simplificada:
- De π rad/s a rpm
 que con la ecuación simplificada:
que con la ecuación simplificada:
Conversiones entre grados y radianes
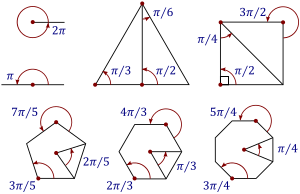
Los grados y los radianes son dos diferentes sistemas para medir ángulos. Un ángulo de 360° equivale a 2π radianes; un ángulo de 180° equivale a π radianes (recordemos que el número π ≈ 3,14159265359…).
Las equivalencias de los principales ángulos se muestran en las siguientes figuras:
Para convertir grados en radianes o viceversa, partimos de que 180° equivalen a π radianes; luego planteamos una regla de tres y resolvemos.
-
- Ejemplo A
Convertir 38° a radianes:
Primero planteamos la regla de tres. Nótese que la x va arriba, en la posición de los radianes.
Despejamos x, también simplificamos.
Por último obtenemos el equivalente decimal:
x = 0,6632 radianes.
-
- Ejemplo B
Convertir 2,4 radianes a grados.
Primero planteamos la regla de tres. Nótese que la x va abajo, en la posición de los grados.
Despejamos x.
Por último obtenemos el equivalente decimal:
x = 137.5099°".
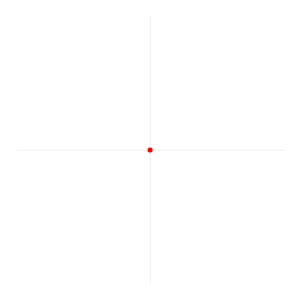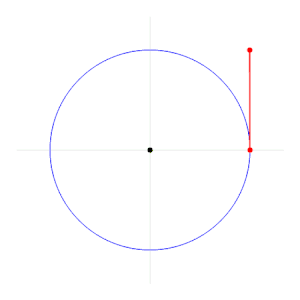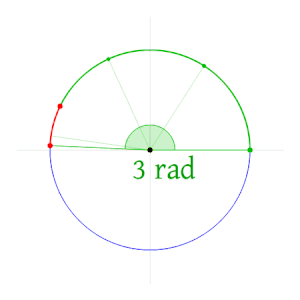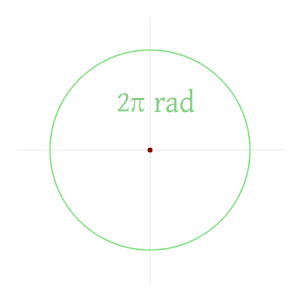
Un ángulo de 1 radián corresponde al arco de circunferencia cuya longitud es su radio. Una circunferencia completa corresponde a 2π radianes.
Segundo sexagesimal, segundo de arco o arcosegundo es una unidad de medida angular. Su valor equivale a 1/60 del minuto de arco y a 1/3600 del grado sexagesimal. Su abreviatura estándar es la doble prima (″), de forma que un arcosegundo se escribiría 1″. También pueden usarse las abreviaturas asec o arcsec. No deben confundirse esta última con la abreviación de la función trigonométrica arcosecante, siendo ambas abreviaturas idénticas (arcsec).
Uso astronómico
Dado que las estrellas se encuentran tan lejanas, que sus posiciones relativas no dependen del observador situado en la Tierra, sin importar las distancias reales a las que se encuentre, se utiliza un sistema angular para indicar la posición de ellas. El 'segundo de arco' es útil cuando se trabaja con objetos que no se encuentren muy lejanos de la Tierra, o sobre grupos mayores de estrellas, ya que es una medida demasiado grande para mediciones precisas. Para estas se ocupa los milisegundo de arco (msa, mas); microsegundo de arco (μsa, μas), etc, que entregan mayor precisión.
Parsec
El parsec es una unidad astronómica de longitud, igual a la distancia de un cuerpo celeste desde el que se viera el semieje mayor de la órbita terrestre con un ángulo de un segundo de arco. Equivale a 3,26 años luz (símb. pc). Un objeto visto a unas 206.265 veces su diámetro forma un segundo de arco. Un pársec es una medida de distancia que se define como la distancia a la que debería estar un objeto de una unidad astronómica de diámetro, para que al ser observado mostrara una paralaje de un arcosegundo. El pársec o parsec (símbolo pc) es una unidad de longitud utilizada en astronomía. Su nombre se deriva del inglés parallax of one arc second (paralaje de un segundo de arco o arcosegundo). En sentido estricto pársec se define como la distancia a la que una unidad astronómica (ua) subtiende un ángulo de un segundo de arco (1"). En otras palabras, una estrella dista un pársec si su paralaje es igual a 1 segundo de arco. De la definición resulta que: 1 pársec = 206.265 ua = 3,2616 años luz = 3,0857 × 1016 m.





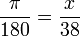

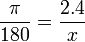

No hay comentarios:
Publicar un comentario