AMIGOS PARA SIEMPRE: Unidades de medida

Unidades de densidad

La densidad de Planck es la unidad de densidad, denotada por ρ_P, en el sistema de unidades naturales conocido como las unidades de Planck.

\rho_P = \frac{m_P}{l_P^3} = \frac{c^5}{\hbar G^2} \; \approx \; 5.1 \times 10^{96} \; \cfrac{kg}{m^3}

donde

m_P es la masa de Planck

l_P es la longitud de Planck

c es la velocidad de la luz en el vacío

\hbar

es la constante reducida de Planck

G es la constante de gravitación universal

Esta unidad es enorme. Equivale aproximadamente a 10²³ masas solares comprimidas en el espacio de un solo núcleo atómicos. Se piensa que, una unidad de tiempo de Planck después del Big Bang, la densidad del universo era de aproximadamente una unidad de densidad de Planck.

Cuando una estrella agota su combustible nuclear de hidrógeno y se sale de la secuencia principal, comienza una carrera desesperada para lograr estabilizarse. Es que el colapso debido a la gravedad, a causa del peso de las capas exteriores, hace que la estrella se derrumbe sobre sí misma. La manera en que este colapso se detiene es que exista una fuerza o presión interna que lo detenga. Mientras la estrella está "quemando" combustible nuclear: fusión de hidrógeno, helio, carbono, oxígeno…, la presión de radiación es la que detiene el colapso. Para una estrella cuya masa final, luego de perder mucha materia expulsándola al espacio, sea inferior a las 1,44 masas solares (límite de Chandrasekhar), la presión generada por el principio de exclusión entre electrones hace que el colapso se detenga. Teóricamente, esta materia se mantiene estable gracias al principio de exclusión entre partículas subatómicas de Wolfgang Pauli. En concreto, esta estrella es denominada enana blanca, y se estabiliza a partir al principio de exclusión entre electrones.

Pero si la estrella remanente, habiendo agotado el combustible nuclear, llega a poseer más de 1,44 masas solares; el colapso continuará ocurriendo hasta llegar a un nuevo tipo de estabilidad, ahora entre neutrones. Una estrella de este tipo se denomina estrella de neutrones y se mantiene rígida y estable gracias al principio de exclusión de Pauli para neutrones.

By NASA/Swift/Mary Pat Hrybyk-Keith and John Jones [Public domain]

Rayos gamma provenientes de colapso estelar (ilustración)

Ahora bien, Si el núcleo de neutrones, también denominado neutronium, posee una masa por debajo de las 3 masas solares, permanecerá así en este estado degenerado. Si, por el contrario, el neutronium supera ese límite, denominado Límite de Tolman-Oppenheimer-Volkoff, el núcleo no soportará su propia gravedad y continuará colapsando hasta llegar al punto de convertirse en una estrella de Planck

Este tipo de estrellas, según un trabajo reciente de Carlo Rovelli, Francesca Vidotto y titulado Planck stars, se mantendrían estables por sí solas, sin ningún tipo de presión interna. Es decir, este estado de la materia, el más denso posible, mantendría a cualquier objeto de manera rígida por más masa que tuviese. De esta forma se evitaría llegar a una singularidad, donde la densidad sería infinita.

La existencia de una estrella de Planck sería muy efímera desde un sistema de referencia situado en la estrella misma, pero debido a la intensa gravedad reinante en ella, para un sistema de referencia exterior esta estrella viviría lo suficiente (por dilatación temporal) como para permitir que el agujero negro se evaporase a partir de la radiación de Hawking.

Como se puede apreciar, la existencia de una estrella de Planck no niega la existencia de un agujero negro, pues la gravedad en la superficie de esta estrella sería lo suficientemente intensa como para no permitir que la radiación electromagnética escape.

Una estrella de Plack posee una densidad igual a la densidad de Planck, la cual sería la más alta posible para la materia en este Universo y la que reinaba en el tiempo de Planck, una vez ocurrido el Big-Bang. Para calcular la densidad de Planck simplemente se ha de dividir la masa de Planck sobre la longitud de Planck elevada al cubo. Para obtener los tres valores de densidad, tiempo y masa de Planck se puede recurrir al análisis dimensional como se ve a continuación.

Ahora, para obtener la densidad de Planck, dividimos, como se dijo, masa sobre longitud elevada al cubo:

Donde dice el signo = se puede y se debe reemplazar por un aproximado. De esta manera la presión cuántica contrarrestaría el colapso gravitatorio de la estrella.

Según los autores del trabajo, el radio de una estrella de Planck sería el indicado en la ecuación de la siguiente imagen:

DPCM es un codificador de forma de onda que parte de la base de PCM pero añade algunas funcionalidades basadas en la predicción de las muestras de la señal. Se parte de una señal analógica (continua en el tiempo) la cual se quiere codificar. El primer paso a realizar es el proceso de muestreo (tomar el valor de la señal cada cierto período regular de tiempo). Con eso se consigue una señal discreta en el tiempo (compuesta por toda una serie de muestras equiespaciadas). El siguiente paso es la cuantificación: se preestablecen unos niveles (amplitudes) y (2 opciones):

[opción 1] se coge el valor de dos muestras consecutivas, se resta el valor de la segunda menos la primera, se cuantifica el resultado y finalmente se codifica, o bien
[opción 2] se hace la predicción de una muestra a partir de las muestras anteriores y se calcula la diferencia entre el valor de la muestra actual real y la predicción (el resultado es el error de predicción), se cuantifica el error y se codifica.

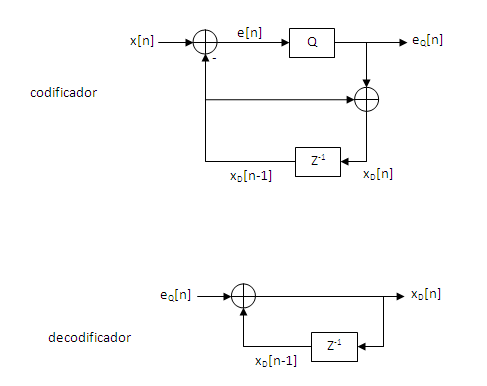
Aplicando uno de estos dos procesos se elimina la redundancia de la señal a corto término y se consiguen factores de compresión del orden de 4 (el tamaño del fichero se divide por 4). El motivo por el cual se reduce el tamaño del fichero es porque como se hace la diferencia entre dos muestras, el resultado será un valor pequeño y hasta cercano a cero y, por lo tanto, en codificación se necesitarán menos bits. En resumen, se puede decir que la potencia de la señal “diferencia” es mucho menor que la de la señal discreta original. A continuación se presentan los diagramas del codificador y decodificador de las dos versiones comentadas:

Opción 1 (diferencia entre dos muestras consecutivas)

Versión 1

El codificador hace la función de diferenciador (también conocido como derivador), mientras que el decodificador actúa como un acumulador (también integrador) El cuantificador (Q) reduce el número de bits mientras que el cuantificador inverso (

Q^{-1}

) recupera el número de bits original de la señal discreta inicial.

Versión 2 [Análisis-por-síntesis]

Incorporación del decodificador dentro del propio codificador

Opción 2 (predicción de la muestra actual)

Incorporación de un predictor lineal

escala Baumé es una escala usada en la medida de las concentraciones de ciertas soluciones (jarabes, ácidos). Fue creada por el químico y farmacéutico francés Antoine Baumé (1728–1804) en 1768 cuando construyó su aerómetro. Cada elemento de la división de la escalera Baumé se denomina grado Baumé y se simboliza por ºB o ºBé.

La graduación de un aerómetro en grados Baumé se establece en referencia a una disolución acuosa de cloruro de sodio (NaCl) al 10% en masa y agua destilada. Se marca el valor 0 para el agua destilada y el valor 10 para la disolución al 10%, y se divide el espacio entre ambos en 10 grados Baumé. La escala se puede alargar por abajo para líquidos menos densos que el agua destilada (ρ=1 g/cm³). Para líquidos más densos que el agua la escala es un poco diferente: se mantiene el valor 0ºBé para el agua destilada y se pone el valor 15ºBé cuando el aerómetro está dentro de una disolución al 15% de cloruro de sodio. Esto hace que las dos escalas no se correspondan; por ejemplo los 25ºBé (densidad alta) no coinciden con los 25ºBé (densidad baja), y por esta razón se la considera una escala confusa.

La relación entre la densidad, ρ, de la disolución y los grados Baumé se ha expresado de diversas formas durante el tiempo que se ha empleado. Actualmente a 20ºC la relación entre la densidad, ρ, y los grados Baumé de una disolución viene dada por las siguientes relaciones:¹

Para líquidos más densos que el agua (ρ > 1 g/cm³):
ºBé = 145 – 145/ρ
ρ = 145/(145 - ºBé)
Para líquidos menos densos que el agua (ρ < 1 g/cm³):
ºBé = 140/ρ – 130
ρ = 140/(130 + ºBé)

Su ventaja es que permite evaluar la concentración de cualquier solución con una misma unidad (grados Baumé) y un mismo aparato (elaerómetro Baumé), pero hace falta emplear una tabla específica para determinar la concentración de cada tipo de sustancia. Se sigue empleando en la actualidad en la producción industrial de cerveza, vino, miel y ácidos concentrados.

Los grados Baumé se relacionan con la gravedad especifica (GE) de la misma forma, se debe tomar en cuenta que la temperatura de referencia es de 60 °F en lugar de 4 °C: GE((60°)/(60°))F.

Para líquidos más pesados que el agua:
GE = 145/(145 - ºBé)
Para líquidos más ligeros que el agua:
GE = 140/(130 + ºBé)

Con base en la escala Baumé, el American Petroleum Institute (API) desarrolló una escala un poco diferente. Las fórmulas son:

Para líquidos más ligeros que el agua:
GE = 141.5/(131.5 + ºAPI)
API = (141.5/GE) - 131.5)
La escala Baumé es una escala que mide las concentraciones de ciertas soluciones (jarabes, ácidos, etc.). Fue creada por el químico y farmacéutico francés Antoine Baumé. Un grado Baumé equivale a 17 gramos de azúcar por litro o peso potencial del mosto -que son conceptos equivalentes- ya que 17 gramos de azúcar por litro producen un grado de alcohol.

Por su parte la escala Brix expresa el porcentaje de azúcar en peso dentro de una solución a una temperatura dada. Un grado brix corresponde a 1% en peso de azúcar.

Un grado Brix es la densidad que tiene (a 20° C) una solución de sacarosa al 1 %, y a esta concentración corresponde también a un determinado índice de refracción (el índice de refracción de un medio es el cociente entre la velocidad de la luz en el vacío ( 3.108 m/s ) y la velocidad de la luz en ese medio, no tiene unidades y siempre es mayor o igual que 1).

De acuerdo a esta definición tenemos varios elementos que comprender:

1.-) densidad = Relación entre la masa y el volumen de una sustancia o cuerpo

2.-) “que tiene a (20° C)” o sea temperatura = Grado mayor o menor de calor de un cuerpo o de la atmósfera

3.-) solución de sacarosa al 1% o sea azúcar = solución de azucar

4.-) Índice de refracción = determina la reducción de la velocidad de la luz al propagarse por un medio homogéneo

Una vez desglosado el concepto, es importante es entender que:
- Cuánto mayor sea la concentración de los azúcares de un mosto, más denso será éste y menor la velocidad con que la luz lo atraviese, provocando un cambio en el índice de refracción. (Así se puede establecer una relación entre la concentración de azúcar y el índice de refracción)
- El índice de refracción varía con la temperatura.
- Un mosto tiene una concentración de sólidos solubles disueltos de un grado Brix, cuando su índice de refracción sea igual al de una solución de sacarosa al 1 % ( p/v ).
- Como los sólidos no son solamente sacarosa, sino que hay otros azúcares, ácidos y sales, un grado Brix no equivale a una concentración de sólidos disueltos de 1g/10ml (sino, sólo de azúcares).
- Para determinar los grados Brix se usa un aparato llamado refractómetro de ABBE, es el más común y mide los índices de refracción de cualquier producto. (El refractómetro es un instrumento que se usa para determinar el contenido en azúcar midiendo el índice de refracción del mosto).
- Para determinar los grados Baumé se utiliza un densímetro que posee su escala en “grados Baumé” y que se llama aerómetro.
La relación entre ºBrix y ºBaumé se refleja de la siguiente manera:

Los grados Baumé ºBe se multiplica por 1,8 (aproximadamente) para determinar los grados ºBrix:

º Be x 1,8 = º Brix 10º Be x 1,8 = 18º Brix

Ahora bien, ¿cuál es su importancia dentro del mundo de vino? Hay muchas razones, algunas de ellas es que a través de estas escalas se mide -por ejemplo- la madurez de la uva y sus índices de azúcar (lo que posteriormente se transformará en grados alcohólicos) lo cual puede influir a su vez, en la fecha de la vendimia, tipo de fermentación, etc. Estas escalas también se utilizan para controlar los mostos en fermentación, como por ejemplo en los vinos de Oporto donde se corta la fermentación (añadiendo alcohol vínico) cuándo ésta alcanza los 7 u 8 grados Baumé.