División de Voltaje y de Corriente
División de voltaje
Se usa para calcular el voltaje de alguno de los resistores que se han unido en un arreglo en serie, en función del voltaje del arreglo. Si no hay resistores en serie no es posible aplicar divisor de voltaje.
Dos resistores en serie
En un arreglo en serie, el voltaje menor se localiza sobre el resistor menor.
N resistores en serie
Si la red se generaliza a N resistores en serie se tiene:}
Dos resistores en serie del mismo valor
Para dos resistores del mismo valor se tiene:
Tres resistores en serie del mismo valor
Para tres resistores del mismo valor se tiene:
Fracción de voltaje
Se puede tomar una fracción cualquiera del voltaje de la fuente colocando de forma adecuada resistores en serie. Es decir, si se requiere obtener 1/3 del voltaje de la fuente se colocan tres resistores en serie, y se toma el voltaje de uno de ellos.
Si se requiere 4/5 del voltaje de la fuente se configura así:
Se conectan 5 resistores en serie, y se toma el voltaje de salida sobre 4 de ellos.
Ejemplo 1 Divisor de voltaje
La división de voltaje y la reducción de resistores pueden aplicarse simultáneamente.
División de corriente
El dual de la división de voltaje es la división de corriente.
Se usa para calcular la corriente de alguno de los resistores que se han unido en un arreglo en paralelo, en función de la corriente del arreglo. Si no hay resistores en paralelo, no es posible aplicar la división de corriente.
Dos resistores en paralelo
En un arreglo en paralelo, la corriente menor circula siempre por el resistor mayor.
Dos conductancias en paralelo
N resistores en paralelo
Dos resistores en paralelo del mismo valor
Tres resistores en paralelo del mismo valor
Fracción de corriente
Se puede tomar una fracción cualquiera de la corriente de la fuente colocando de forma adecuada resistores en paralelo. Es decir, si se requiere obtener 1/5 de la corriente de la fuente se conectan cinco resistores en paralelo, y se toma la corriente de uno de ellos.
Ejemplo 1 división de corriente
Uso simultáneo de la división de corriente y la reducción de resistores
Resumen divisor de voltaje vs divisor de corriente
Ejemplo 2 divisor de voltaje y de corriente
- Use métodos de reducción de resistencias para hallar Req
- Use división de corriente para calcular I1
- Use división de voltaje para calcular Vs
- Use división de corriente para calcular I3
Un divisor de tensión es una configuración de circuito eléctrico que reparte la tensión de una fuente entre una o más impedanciasconectadas en serie.
Supóngase que se tiene una fuente de tensión  , conectada en serie con n impedancias.
, conectada en serie con n impedancias.
 , conectada en serie con n impedancias.
, conectada en serie con n impedancias.

Sustituyendo la segunda ecuación en la primera se obtiene que el voltaje en la impedancia genérica 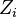 será:
será:
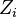 será:
será:
Obsérvese que cuando se calcula la caída de voltaje en cada impedancia y se recorre la malla cerrada, el resultado final es cero, respetándose por tanto la segunda ley de Kirchhoff.
Un circuito análogo al divisor de tensión en el dominio de la corriente es el divisor de corriente.
Divisor de corriente resistivo
Una fórmula general para la corriente IX que atraviesa una resistencia RX que está en paralelo con otras resistencias de resistencia equivalente RT, según la Figura 1 es:

donde IT es la corriente total entregada por la fuente. Obsérvese que si RT representa una combinación en paralelo de varias resistencias Ri (i=1, 2, ...) la resistencia equivalente se expresa como:
Caso general
Aunque es común el divisor resistivo, éste también puede ser elaborado con impedancias que dependen de la frecuencia de la señal alimentada a la red divisora como se muestra en la Figura 2. En el caso general, la corrienteIna través de una impedancia Zn se expresa como:

La corriente que circula por cada impedancia es el producto de la corriente proporcionada por el generador por todas las demás impedancias (es decir, todas menos por la que pasa la corriente que queremos calcular) dividido entre la suma de todas las posibles combinaciones de productos de impedancias en grupos de n-1 en n-1:

Que también se puede escribir como:

Uso de admitancias
Las ecuaciones se simplifican bastante si trabajamos con admitancias en lugar de impedancias, sabiendo que :

quedando la expresión de la siguiente forma:





































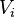 en la impedancia genérica
en la impedancia genérica 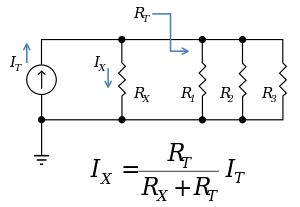


No hay comentarios:
Publicar un comentario