Paralajes Fotométricas y Espectroscópicas
Cuando las estrellas están más lejos y su paralaje es tan pequeña que no se puede medir, usamos mediciones indirectas basadas en el conocimiento de los tipos espectrales o la fotometría de esas estrellas.Ciertos tipos de estrellas tienen el brillo bien determinado, y pueden ser usados como indicadores de distancias. Las más útiles son als estrellas pulsantes RR Lyrae y Cefeidas. Usando sus curvas de luz se puede encontrar una relación muy precisa entre los períodos y las luminosidades de estas estrellas.
Estrellas pulsantes P - L
Curvas de luz
no existe un método único que nos permita medir las distancias en el cosmos. Dependiendo de la distancia que nos separe del objeto, hay que utilizar uno distinto, y éstos necesitan verificar su funcionamiento con otro anterior, lo que nos lleva a una especie de escalera de métodos que nos permitirían ir de los alrededores del Sol (estrellas más cercanas) hasta las mayores distancias conocidas, al borde del universo visible.
Otra división posible de estos métodos es si el método permite medir distancias de forma directa (estaríamos hablando de medidores primarios) o necesita apoyarse en algún método primario para realizar la medición (en este caso hablaríamos de medidores secundarios).
En esta primera entrega describiremos los medidores primarios.
Tipos de medidores
Hay dos grandes grupos de medidores, según la propiedad física de aprovecha para hallar la distancia al objeto:
- Candelas
- Reglas
Las candelas aprovechan las leyes físicas que gobiernan la emisión de energía que producen los objetos astronómicos. La energía de esos objetos la recibimos en forma de radiación electromagnética, que podemos medir. Si por alguna propiedad de los objetos podemos también calcular su luminosidad intrínseca, estas dos magnitudes están relacionadas en una expresión que contiene la distancia al objeto. Con lo que podemos hallarla finalmente. Esta expresión es la siguiente:
F = L / (4*pi*D2)
Donde F es el flujo, medido en la Tierra, L su luminosidad y D la distancia al objeto.
Las reglas aprovechan la geometría para hallar la distancia. Si obtenemos el tamaño aparente de un objeto al telescopio o en una fotografía, y sabemos por algún otro motivo su tamaño real, utilizando la geometría podemos relacionar estas dos magnitudes con la distancia que nos separa de ellas. Para ángulos pequeños la expresión que relaciona estos parámetros es
q = T / D
Donde q es el tamaño del objeto visto desde la Tierra, T su tamaño real y D la distancia que nos separa de él.
Medidores primarios
Los siguientes métodos están en el grupo de los primarios, describiremos uno a uno su metodología
- Paralaje trigonométrico
- Método de los cúmulos en movimiento
- Método del punto de convergencia
- Ajuste de secuencia principal
- Estrellas variables: Cefeidas y RRLyrae
- Paralaje espectroscópico
Los tres primeros métodos son reglas, mientras que los tres últimos son candelas.
Paralaje trigonométrico
En este método se utiliza el fenómeno de la paralaje en dos observaciones separadas seis meses de un objeto relativamente cercano enfrentado al fondo “fijo” del cielo. Se resuelve el triángulo rectángulo de la figura, donde se conoce el ángulo de paralaje (mitad del desplazamiento medido entre las dos observaciones separadas 6 meses) y la distancia Tierra-Sol (150 millones de kilómetros) por trigonometría simple se resuelve la cantidad D, distancia que nos separa del objeto.
En el ejemplo de la figura, se está midiendo la unidad patrón, el parsec, que da un ángulo de paralaje de 1”
Este método es válido sólo para estrellas cercanas. Los mejores datos disponibles, provenientes del satélite Hipparcos, alcanzan a estrellas distantes 200 pc con un error medio para esa distancia del 20%. Estos datos serán mejorados con el lanzamiento de la misión GAIA.
Método de los cúmulos en movimiento
Este método está basado en la variación que sufre con el tiempo el diámetro de un cúmulo debido a su movimiento radial relativo al Sol. A partir del diámetro angular del cúmulo, su velocidad radial y la variación del diámetro con el tiempo, se obtiene la distancia.
Este método también se restringe a distancias relativamente próximas, en las que las variaciones de tamaño de los cúmulos abiertos son apreciables, que se acota a los alrededores del brazo de nuestra galaxia.
Método del punto de convergencia
Este método aprovecha la propiedad que tienen todas las estrellas que pertenecen a un mismo cúmulo abierto, es decir, que han nacido de la misma nube de hidrógeno primigenia. Por este hecho, todas las estrellas de un mismo cúmulo comparten en sus primeros tiempos, la misma dinámica (todas las estrellas llevan la misma dirección de desplazamiento). Observados desde la Tierra, estas estrellas parecen converger en un punto.
Si se conoce las dos componentes de la velocidad de las estrellas del cúmulo (tangencial y radial), se puede calcular la distancia que nos separa del cúmulo.
La imagen de arriba corresponde al estudio del cúmulo de las Hyades mediante este método y la estimación de su punto de convergencia.
Ajuste de secuencia principal
Es un método que utiliza la fotometría de dos grupos de estrellas que pertenezcan a la secuencia principal y que estén a dos distancias diferentes (por ejemplo, pertenecientes a dos cúmulos diferentes). De uno de los cúmulos se conoce ya su distancia. Al representar los dos grupos de estrellas en el diagrama HR, se puede apreciar dos franjas diferenciadas de secuencia principal, perteneciente una a cada cúmulo. Las dos franjas están separadas en la gráfica verticalmente, que corresponde a una magnitud dm=M-m. La franja de secuencia principal más baja, que corresponde al cúmulo más lejano, estará 10 0.2dm más lejos.
Estrellas variables: Cefeidas y RR Lyrae
Es el método principal, más fructífero y exacto de cálculo de distancias de estrellas de nuestra galaxia y de galaxias espirales próximas. Utiliza el método de candela, calculando magnitudes aparentes y absolutas de este tipo de estrellas. Las magnitudes aparentes se calculan por fotometría y las absolutas se calculan por una propiedad física típica de cada uno de los tipos de estrellas variables.
La primera descubierta fue la de las Cefeidas, realizada por la astrónoma Henrietta Leavitt en 1907. Se descubrió que hay una ley matemática que relaciona el periodo de la variable con su magnitud absoluta. Concretamente:
M = -2.78 log(P/10) – 4.13
Posteriormente se descubrió otra relación muy similar para las RR Lyrae.
El procedimiento sería el siguiente:
- Calcular la magnitud aparente media (m) por fotometría.
- Estudiar la variación de brillo, mediante la observación continua de su brillo, extraer de esas observaciones el periodo de pulsación.
- Aplicar la fórmula de arriba para calcular su magnitud absoluta (M).
- Aplicar la fórmula de las candelas m – M = 5 log (d/10) para calcular la distancia a la cefeida.
Los periodos de las RR Lyrae son de 12 a 24 horas, mientras que los de las cefeidas de 2 a 150 días. Las ventajas del método de las cefeidas son que son fácilmente distinguibles, son muy luminosas, lo que permite encontrar cefeidas hasta en galaxias a 5 MPc.
Aquí podéis apreciar la curva de luz típica de una cefeida.
Paralaje espectroscópico
Los dos métodos anteriores necesitaban de la fotometría de la estrella. En este último método se utiliza la espectroscopía de la luz que proviene de la estrella y el diagrama HR que distribuye las estrellas según su temperatura y su clase de luminosidad. La espectroscopía estelar es el estudio de las propiedades de una estrella estudiando su espectro, que es la distribución de la luz que recibimos de esa estrella separada por longitud de onda. Por la posición y número de las líneas de absorción del espectro podemos averiguar qué tipo espectral posee (O, B, A, F, G, K, M, L). Esto equivale a saber su temperatura superficial y a poderla colocar en el eje X del diagrama HR. Del mismo modo, la anchura de las líneas espectrales nos habla de la clase de luminosidad (I – Supergigantes, II – Gigantes brillantes, III – Gigantes, IV – Subgigantes, V – Enanas, VI – Enanas blancas). Esta clasificación nos permite colocar a la estrella en el eje Y del diagrama HR. Una vez colocada, podemos hacer corresponder esa posición con una luminosidad absoluta. Finalmente con la fórmula de las candelas estándar, podremos calcular la distancia que nos separa de ella.
El principal inconveniente de esta técnica es que como mucho se obtiene una precisión de 0,7 a 1,25 magnitudes en la magnitud absoluta, lo que puede llegar a una imprecisión del 60% en la distancia. Este problema se puede minimizar calculando el diagrama HR para estrellas de un mismo cúmulo, que por tener las estrellas con tipos espectrales parecidos, se minimiza el error.
paralaje estelar al efecto de paralaje en las estrellas distantes. Es paralaje en una escala interestelar, y puede ser utilizado para determinar la distancia desde la Tierra a otra estrella en forma directa utilizando astrometríade precisión. Este tema fue durante siglos un tema sumamente debatido en la astronomía, pero era tan difícil de establecer que sólo a comienzos del siglo XIX pudo lograrse medir para las estrellas más próximas. Aún en el siglo XXI, las estrellas para las que se han podido realizar mediciones de paralaje son aquellas que se encuentran relativamente cercanas en la escala galáctica, y la mayoría de las mediciones de distancia se realizan utilizando corrimiento al rojo u otros métodos.
La paralaje es por lo general producto de las diferentes posiciones que ocupa la Tierra en suórbita, que hace que las estrella próximas parezca se desplazan con respecto a las estrellas más distantes. Al observar la paralaje, midiendo ángulos y utilizando elementos de geometría, se puede determinar la distancia a distintos objetos en el espacio, como ser estrellas y planetas.
A causa de que las otras estrellas se encuentran muy distantes, el ángulo a medir es pequeño y se puede utilizar la aproximación paraxial, por lo que la distancia a un objeto (medida enparsecs) es la recíproca del paralaje (medido en segundos de arco):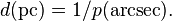 
Por ejemplo, la distancia a Proxima Centauri es 1/0.7687=4.243 ly.1 La primera medición con éxito de una paralaje estelar la realizó Friedrich Bessel en 1838 sobre la estrella 61 Cygniutilizando un heliómetro de Fraunhofer en el Observatorio de Königsberg.
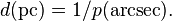Por ejemplo, la distancia a Proxima Centauri es 1/0.7687=4.243 ly.1 La primera medición con éxito de una paralaje estelar la realizó Friedrich Bessel en 1838 sobre la estrella 61 Cygniutilizando un heliómetro de Fraunhofer en el Observatorio de Königsberg.
La paralaje estelar se suele medir utilizando la paralaje anual, definida esta como la variación en la posición de una estrella vista desde la Tierra y el Sol, es decir, el ángulo subtendido a una estrella desde el radio medio de la órbita de la Tierra alrededor del Sol. El parsec, o pársec, (3.2616 años luz) se define entonces como la distancia para la que la paralaje anual es de unarcosegundo. La paralaje anual se mide normalmente observando la posición de una estrella en diferentes momentos del año a medida que la Tierra se mueve en su órbita. La medición de la paralaje anual fue el primer método fiable para medir la distancia a las estrellas más cercanas. La primera medición con éxito de una paralaje estelar la realizó Friedrich Bessel para la estrella Cygni 61 usando un heliómetro.2 6
Dado que es tan difícil de medir, sólo se había logrado unas 60 paralajes estelares a finales del siglo XIX, la mayoría utilizando un micrómetro astronómico. Los astrógrafos lograron acelerar el proceso mediante la utilización de placas fotográficas astronómicas a principios del siglo XX. La llegada de máquinas de medición de placas automáticas7 y de tecnología informática más sofisticada en la década de 1960 permitió una recopilación más eficiente de catálogos de estrellas. En la década de 1980, los dispositivos de carga acoplada (CCDs) substituyeron a las placas fotográficas y lograron reducir el margen de error hasta un miliarcosegundo.
La paralaje estelar se mantiene como el medio para calibrar otros métodos de medición de laEscalera de distancias cósmicas. El cálculo preciso de la distancia basándose en la paralaje estelar requiere la medición de la distancia entre la Tierra y el Sol, que ahora se obtiene con el reflejo del radar que devuelven la superficie de los planetas.8
Los ángulos que implican estos cálculos son muy pequeños y por ello difíciles de medir. La estrella más cercana al Sol (y por lo tanto la de mayor paralaje) es Próxima Centauri, y tiene una paralaje de 0,7687 ± 0,0003 arcosegundos.1 Este ángulo sería aproximadamente el que subtendería un objeto de 2 centímetros de diámetro situado a 5.3 kilómetros de distancia.
No hay comentarios:
Publicar un comentario