lunes, 4 de abril de 2016

Astronomía y astrofísica

MEDICION DE PROPIEDADES ESTELARES

DETERMINACIÓN DE MASAS

Medidas directas en binarias:
De la tercera ley de Kepler se tiene:


\begin{displaymath}G (M_1 + M_2) = \frac{4 \pi^2 a^3}{P^2} \end{displaymath}


$a = d \: \theta$
P es medido, pero necesitamos calcular a $\longmapsto$ distancia $\longmapsto$ errores . Además debemos conocer la órbita absoluta de una estrella al menos con respecto a las estrellas fijas $\longmapsto$ binarias visuales. 

\begin{displaymath}\frac{M_2}{M_1 + M_2} = \frac{a_1}{a} \end{displaymath}


Existe una relación entre la masa M y la luminosidad L de una estrella: 
Relación M-L: (sólo para estrellas MS) $\: \: \: \: \: \:$ $L \propto M^x$ con $\: \: \: \: \: \: \: x = 4$ para $L > L_{\odot}$ 
x = 2.8 para $L < L_{\odot}$ 
DETERMINACIÓN DE MASAS ATÓMICAS Y MASAS MOLECULARES RELATIVAS



 
La interpretación de los datos volumétricos a la luz de la hipótesis de Avogadro permitió obtener fórmulas correctas de muchos elementos y compuestos, evitando la regla de máxima simplicidad. Adicionalmente, la combinación de estos conocimientos con los resultados del análisis químico también sirvió para obtener masas atómicas y masas moleculares relativas.
 
Síntesis del cloruro de hidrógeno
       
 
 
1 vol. de hidrógeno
 
 1 vol. de cloro
   
2 vol. cloruro de hidrógeno
       
H2
+
Cl2
 
 
2 HCl

 

   

 
Veamos, como ejemplo, la reacción de síntesis del cloruro de hidrógeno, representada en el esquema adjunto. Los resultados experimentales sobre esta reacción informan de que cada gramo de hidrógeno reacciona con 35.5 gramos de cloro. Por tanto, como las moléculas de cloro y de hidrógeno son ambas di-atómicas, se deduce que cada átomo de cloro debería tener una masa 35.5 veces mayor que el de hidrógeno. 
La realidad es un poco más complicada. En la naturaleza se encuentran dos isótopos estables de cloro: uno 35 veces y el otro 37 veces más masivo que el hidrógeno. Estos isótopos tienen unas proporciones relativas de 3:1 respectivamente, lo que da el resultado de una masa atómica relativa para el cloro de 35.5.
 
De los datos de la reacción anterior también se deduce la obviedad de que la molécula de hidrógeno gaseoso (H2) tiene una masa doble que la del átomo de hidrógeno y que la molécula de cloruro de hidrógeno (HCl) debería tener una masa 36.5 (35.5 + 1) veces mayor que la del átomo de hidrógeno.
 
Cannizzaro (1826-1910)
 
Dalton (entre 1803 y 1805), y Berzelius (entre 1808 y 1826), fueron los primeros en determinar masas atómicas y masas moleculares relativas de bastantes elementos conocidos. Dichas masas fueron definidas inicialmente en relación al elemento más ligero, el hidrógeno, al que se atribuyó en esta escala de masas relativas el valor 1. Posteriormente Cannizzaro (1826-1910) refinó estos conceptos aplicando la hipótesis de Avogadro. En un Congreso celebrado en Karlsruhe en 1860, formuló la siguiente ley para determinar las masas atómicas de los elementos: las distintas cantidades del mismo elemento contenido en distintas moléculas son todas múltiplos enteros de la masa atómica.
Cannizzaro determinó experimentalmente masas atómicas y masas moleculares comparando la densidad de vapor de un conjunto de gases con moléculas conteniendo uno o más átomos del elemento químico en cuestión.
 
Sobre la base de estos hallazgos y hasta mediados del siglo XX, los químicos y físicos utilizaron dos escalas de masa atómicas relativas. Los químicos usaban una escala tal que la mezcla natural de isótopos de oxígeno tenía una masa atómica de 16, mientras que los físicos asignaron el mismo número 16 a la masa atómica del isótopo de oxígeno más común (oxígeno-16). Como en el oxígeno natural están presentes el oxígeno-17 y el oxígeno-18, esto conducía a 2 tablas diferentes de masas atómicas relativas.
 
Entre 1959 y 1960 ambas organizaciones acordaron una escala unificada, basada en el carbono-12 (el carbono-12 es el más abundante de los dos isótopos estables del elemento carbono, representando el 98,89% de todo el carbono terrestre). Esta escala cumplía el requerimiento de los físicos de basar la escala en un isótopo puro y a la vez se hacía numéricamente cercana a la escala de los químicos. Atendiendo a esta escala unificada se define:
 
 
Masa atómica relativa: Número que indica cuántas veces mayor es la masa de un átomo con respecto a 1/12 de la masa del isótopo del C-12.
 
Masa molecular relativa: Número que indica cuántas veces mayor es la masa de una molécula de una sustancia con respecto a 1/12 de la masa del isótopo del C-12. Se puede determinar sumando las masas atómicas relativas de los elementos cuyos átomos constituyen una molécula de dicha sustancia.
 
La unidad de masa atómica relativa y de masa molecular relativa se llama Dalton o unidad de masa atómica y se abrevia u (antes uma).



RADIOS ESTELARES

Las estrellas son distantes, y la proyección de sus radios en el cielo es:

\begin{displaymath}f_{obs} = \frac{R^2 F}{d^2} = \frac{\theta^2}{4} F \hspace{3 cm} \theta = \frac{2R}{d} \end{displaymath}

Dadas que son tan importantes, las mediciones de radios estelares se realizan usando distintas técnicas:
$\longmapsto$ Interferometría, estrellas binarias, ocultaciones, flujo infrarojo. 
Para estrellas binarias eclipsantes, tenemos las siguientes relaciones de los eclipses:
Fase $\:$ $\theta = \frac{2 \pi}{P} (t - t_0) \: \: \: $t0 = mínimo primario r1 , r2 = K r1 
\begin{displaymath}l_1 + l_2 = 1 \hspace{2cm} l_{ocul} = l_1 = 1 - l_2 \hspace{2cm} l_{trans} = 1 - K^2 l_1 = 1 - K^2 l_{ocul} \end{displaymath}


\begin{displaymath}K^2 = \frac{1 - l_{trans}}{l_{ocul}} \end{displaymath}

Durante el contacto exterior : 
\begin{displaymath}r_1 + r_2 = r_1 (1 + K) = d(\sin^2 \theta^\prime \sin^2 i \: + \: \cos^2 i)^{1/2} \end{displaymath}


\begin{displaymath}r_1 - r_2 = r_1 (1 - K) = d(\sin^2 \theta^{\prime\prime} \sin^2 i + \cos^2 i)^{1/2} \end{displaymath}

$\longmapsto \frac{d}{r_1} \:, \: \cos i$

\begin{displaymath}d _{(pc)} = \frac{1}{p^{\prime\prime}} = \frac{(M_1 + M_2)^{1/3} P^{2/3}}{a^{\prime\prime}} \end{displaymath}


Curvas de isoradio

El diagrama HR ilustra la luminosidad y temperatura de una estrella. Por otra parte, la ley de radiación del cuerpo negro une la luminosidad de una estrella con su temperatura y radio.
Se deduce que la repartición de los radios estelares en el diagrama HR no se hace al azar. La relación :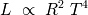
L oc R2 T 4
implica que en el diagrama HR en coordenadas 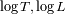logT,log L las líneas de isoradio estelar son rectas de pendiente -4. 
hrrayon.pngrayonstel.png

De las enanas a las gigantes

Lo que precede está en acuerdo con la clase de luminosidades. Se nota que la secuencia corresponde a las estrellas enanas, aunque el radio sea un poco mayor para estrellas calientes. 





DIAGRAMA HERTZSPRUNG-RUSSELL

El diagrama H-R también se conoce como Diagrama Color - Magnitud grafica magnitudes o luminosidad de las estrellas vs colores o temperaturas. este gráfico es muy importante, porque nos permite relacionar parámetros físicos con las observaciones de las estrellas.
Teoría $\longleftrightarrow$ Observación 
$L , T_{eff} \longleftrightarrow V , (B - V)_0$
Para conocer las magnitudes absolutas o luminosidades de las estrellas necesitamos conocer sus distancias, usando:

\begin{displaymath}V - M_V = 5 \log d - 5 \end{displaymath}

La medición de distancias es importante en Astronomía, y le mejor fuente disponible al presente es el catálogo de la misión Hipparcos. Este fué un satélite astrométrico de la Agencia Espacial Europea ESA, que durante un par de años midió paralajes muy precisas de estrellas cercanas (con D<500 pc).
$\longmapsto$ Hipparcos.
Además, para conocer las luminosidades necesitamos las correcciones bolométricas para cada estrella, dada por:

\begin{displaymath}M_V - M_{V \odot} = M_{bol} - M_{bol \odot} - (BC - BC_{\odot}) = 2.5 \log \frac{L}{L_{\odot}} - (BC - BC_{\odot}) \end{displaymath}

Para ello usamos los datos solares como referencia. 
\begin{displaymath}\begin{array}{ccc} magnitud \: visual \: aparente & m_{V\odo... ...olor & B-V & = 0.68 \\ color & U-B & = 0.17 \\ \end{array} \end{displaymath}

ABSORCIÓN INTERESTELAR:
La luz de las estrellas se extingue y se enrojece debido a la absorción de polvo interestelar. La relación entre el color intrínseco de la estrella y su color observado es:

B - V = (B- V)0 + EB- V

Donde EB- V es el enrojecimiento, y la extinción es:
$A(\lambda)$ $A_V = R \: E_{B-V}$ $R \approx 3$. 
En general, la relación entre el color B-V t la temperatura de color para estrellas de la Secuencia Principal (MS) es:
$T_c = \frac{7300}{[(B - V)_0 + E_{B - V}]}$
DIAGRAMA H-R:
Definimos el diagrama H-R, que veremos en detalle más adelante.
  • Secuencia principal $0.1 R_{\odot}$ a $\sim 10 R_{\odot} \longmapsto$ enanas, subenanas.
  • Gigantes $\sim 100 R_{\odot}$, $\: \:$ supergigantes $\sim 1000 R_{\odot}$. Estos radios se obtienen a partir de $L = 4 \pi R^2 \sigma T_{eff} \: ^4$
  • Enanas blancas
  • Enanas marrones
  • Pre-secuencia principal


Las estrellas en el diagrama Herztsprung-Russell

En el diagrama HR, con la temperatura en abscisas y la luminosidad en ordenadas, las estrellas no se distribuyen al azar, sino que pueblan zonas bien definidas. Se distinguen tres zonas : la región de la secuencia principal, una larga banda diagonal que se despliega desde las estrellas luminosas y calientes (azul) hacia las estrellas poco brillantes y frías (rojas); encima, la rama de las gigantes y supergigantes ; y abajo la región poblada por estrellas calientes pero poco luminosas, las enanas blancas. 
hrclasses.png

Las clases de luminosidad

Las diferentes clases de luminosidad están representadas en el diagrama HR. Las líneas que dibujan las diferentes clases de luminosidad corresponden a los valores medios de la magnitud absoluta para un conjunto de estrellas de misma clase de luminosidad. La clase I de las supergigantes se subdivide en dos clases : Ia e Ib con diferentes luminosidades. 

Los ejes del diagrama HR

Las magnitudes físicas que definen los ejes del diagrama HR pueden ser medidas por diferentes parámetros, dando origen a diferentes versiones del diagrama HR.
Los tipos espectrales de una estrella son una medida cualitativa de la temperatura efectiva, este parametros puede por lo tanto ser utilizado en abscisas. Más fácilmente observable, el índice de color también es un medidor de la temperatura. Se llama al diagrama resultante diagrama color-magnitud.
En ordenadas, la magnitud absoluta y la luminosidad son equivalentes.

Los parámetros del diagrama HR
AbscisaTemperatura efectiva - Índice de color - Tipo espectral...
OrdenadaLuminosidad (en W o en luminosidad solar) - Magnitud absoluta ...

Los diferentes parametros en abscisas y ordenadas del diagrama HR

La utilidad del diagrama HR

La representación en diagrama HR tiene múltiples intereses :
  • Tratar un gran numero de estrellas
  • Presentar de forma sintética diversos resultados
  • Distinguir los objetos estelares y revelar la física subyacente
Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)