Electrónica básica

Teorema de Norton

Teorema de Thévenin. Resolveremos el problema anterior usando el teorema de Norton.

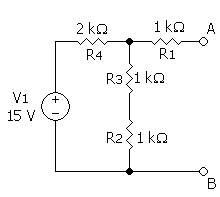
a) Calcular la I_L cuando R_L = 1,5 kW.
b) Calcular la I_L cuando R_L = 3 kW.
c) Calcular la I_L cuando R_L = 4,5 kW.

• Norton.

1. Quitar la carga R_L y poner un cortocircuito (R_L = 0).
   
   
2. Hacemos mallas y calculamos V_Th:
   
   
3.  Cortocircuitar las fuentes de tensión independientes y abrir las fuentes de corriente independientes.
   
4. Unir la carga al circuito equivalente conseguido.
   
   

Ahora aplicando Thévenin es mucho más fácil resolver el problema que teníamos.
a)

b)

c)

El teorema de Norton para circuitos eléctricos es dual del teorema de Thévenin. Se conoce así en honor al ingeniero Edward Lawry Norton, de los Laboratorios Bell, que lo publicó en un informe interno en el año 1926.¹El alemán Hans Ferdinand Mayer llegó a la misma conclusión de forma simultánea e independiente.

Establece que cualquier circuito lineal se puede sustituir por una fuente equivalente de intensidad en paralelo con una impedancia equivalente.

Al sustituir un generador de corriente por uno de tensión, el borne positivo del generador de tensión deberá coincidir con el borne positivo del generador de corriente y viceversa.

Una caja negra que contiene exclusivamente fuentes de tensión, fuentes de corriente y resistencias puede ser sustituida por un circuito Norton equivalente.

Cálculo del circuito Norton equivalente

El circuito Norton equivalente consiste en una fuente de corriente I_No en paralelo con una resistencia R_No. Para calcularlo:

1. Se calcula la corriente de salida, I_AB, cuando se cortocircuita la salida, es decir, cuando se pone una carga (tensión) nula entre A y B. Al colocar un cortocircuito entre A y B toda la intensidad I_No circula por la rama AB, por lo que ahora I_AB es igual a I_No.
2. Se calcula la tensión de salida, V_AB, cuando no se conecta ninguna carga externa, es decir, cuando se pone una resistencia infinita entre A y B. R_No es ahora igual a V_AB dividido entre I_No porque toda la intensidad I_No ahora circula a través de R_No y las tensiones de ambas ramas tienen que coincidir ( V_AB = I_NoR_No ).

Circuito Thévenin equivalente a un circuito Norton

Para analizar la equivalencia entre un circuito Thévenin y un circuito Norton pueden utilizarse las siguientes ecuaciones:

Ejemplo de un circuito equivalente Norton

Paso 1: El circuito original

Paso 2: Calculando la intensidad de salida equivalente al circuito en cuestión

Paso 3: Calculando la resistencia equivalente al circuito en cuestión

Paso 4: El circuito equivalente

En el ejemplo, I_total viene dado por:

Usando la regla del divisor, la intensidad de corriente eléctrica tiene que ser:

Y la resistencia Norton equivalente sería:

Por lo tanto, el circuito equivalente consiste en una fuente de intensidad de 3.75mA en paralelo con una resistencia de 2 kΩ

Paso de circuito Thévenin a circuito Norton y de circuito Norton a circuito Thévenin

Paso de circuito Thévenin a circuito Norton

Tenemos el circuito siguiente:

Cortocircuitamos la carga (R_L) y obtenemos el valor de la intensidad Norton, la R_N es la misma que la R_Th.

Paso de circuito Norton a circuito Thévenin

Tenemos este circuito:

Abrimos la carga (R_L) y calculamos la V_Th, la R_Th es la misma que la R_N.