Campo eléctrico
Cuando vemos un objeto pensamos en él como "un todo" simplemente masa, y todos sabemos que esta masa está compuesta por átomos. Si penetramos un poco más adentro de la estructura tenemos que los átomos están constituidos por dos partes básicas, los electrones y el núcleo y aquí hay que tener en cuenta que estos elementos mas internos tienen otra característica, la carga eléctrica. Las cargas eléctricas de ambas partes generan fuerzas que mantienen la integridad del átomo.
Una particularidad de las cargas eléctricas es que pueden ser de dos signos, y, que su signo determina la dirección de las fuerzas de interacción entre ellas. El átomo es eléctricamente neutro, los electrones tienen una carga que se ha convenido en asumir negativa, mientras el núcleo tiene una carga resultante de igual magnitud pero de signo contrario o positiva.
La evidencia que condujo al descubrimiento de las cargas eléctricas y de las fuerzas eléctricas depende más de las propiedades de la masa en su conjunto y solo indirectamente al hecho de que la materia está constituida por átomos. La propiedad más importante de los cuerpos para el caso que nos ocupa es su conductividad eléctrica, esto es, la facilidad con la que los electrones se pueden desplazar dentro del material. En términos generales y sin entrar en exactitudes las propiedades eléctricas de los diferentes materiales los separan en dos grupos: aquellos en los que las cargas negativas (electrones) se trasladan con facilidad y que se denominan conductores y los que el movimiento de los electrones es difícil, losaisladores.
Cuando frotamos un material aislador con otro del mismo tipo, por ejemplo, una varilla de teflón con un trozo de piel con sus pelos, la barra de teflón adquiere una carga eléctrica mientras que la piel adquiere una carga igual pero de sentido contrario. Esto hace suponer que se han transferido electrones de un cuerpo al otro y por lo tanto se ha perdido la neutralidad. En realidad, en el experimento, el teflón ha quedado con un exceso de electrones, está cargado negativamente y la piel con una deficiencia por lo que su carga será positiva, pero recuerde que esto es convencional por lo que es irrelevante para los resultados.
Ahora asumimos que tenemos una pequeña bola de corcho a la que transferimos la carga del teflón y otra, que hacemos lo mismo con las cargas del trozo de piel. Ambas bolas las colgamos de sendos hilos y las acercamos, el resultado será una fuerza de atracción entre ellas aun sin tocarse. Pero si transferimos a las dos bolas las cargas desde uno de los cuerpos, es decir del teflón o de la piel, al acercarlas se produce el efecto contrario se repelen, es decir en ambos casos hay una fuerza interactuando entre los cuerpos. Este comportamiento da la primera conclusión sobre los cuerpos cargados de electricidad:
El concepto de la acción a distancia, donde una fuerza podía actuar a través de un espacio abierto, incluso en el vacío, fue siempre difícil de aceptar. La acción a distancia sugería que de alguna manera debía llegar la fuerza creada por uno de los cuerpos al otro. Michael Faraday sugirió una vía para resolver esta dificultad, el primer cuerpo influye en el espacio que lo rodeaba por un campo que estaba presente, aunque el otro cuerpo existiera o no, dando origen al concepto de campo eléctrico. En la figura 1 se muestra una visualización del campo eléctrico usando hilos muy finos que flotan en aceite alrededor de una pequeña esfera cargada.
Observe que los hilos se orientan radialmente a la esferita cargada representada en negro en el centro, lo que indica que el campo eléctrico es radial y uniforme en todas direcciones (en la figura se ve en un plano pero en realidad es tridimensional). La orientación de los hilos sugirió un concepto muy útil, las lineas de fuerza. Es decir, se supuso que del centro del cuerpo cargado partían en todas direcciones unas lineas que representaban una fuerza y por lo tanto con una dirección definida. Se asumió dirigidas hacia afuera las lineas de fuerza que salen de un cuerpo cargado positivo y hacia adentro las de uno cargado negativo.
En resumen:
Un cuerpo cargado eléctricamente tiene a su alrededor un espacio de influencia que se denomina campo eléctrico y que al interactuar con otro cuerpo cargado adquiere la naturaleza de una fuerza.
* Se usa el símbolo ≡ para indicar que es una definición. Los símbolos ∣...∣ se usan para indicar que se refiere solo a la magnitud sin tener en cuenta el signo.
La definición está referida a la magnitud (intensidad) del campo eléctrico cuya unidad en el sistema internacional (SI) es newton por coulomb (N/C), sin embargo, el campo eléctrico es una cantidad vectorial y:
Observe que E en la figura 2a, dada la definición, es horizontal y hacia la derecha. Sin embargo, en la figura 2b es horizontal y hacia la izquierda debido a que la carga pequeña positiva recibe una fuerza de atracción hacia el cuerpo con carga negativa grande.
Note algo importante, en ambos casos nos referimos a una carga de prueba pequeña y debe ser así para que la definición realmente funcione. Veamos:
Considere el uso de la esfera de prueba con carga q0 de la figura 3 colocada en el punto P en las inmediaciones del cuerpo que produce el campo eléctrico cuya intensidad queremos determinar, esta esfera de prueba con carga relativamente grande influye sobre la distribución de las cargas en la esfera que produce el campo eléctrico, y la consecuencia de esta reorganización es que la fuerza ejercida sobre la carga de prueba resulta diferente a lo que debía ser si no se hubieran reorganizado. Por lo tanto, la intensidad de campo eléctrico medido difiere del que existe en realidad en ausencia de la carga de prueba, lo que significa que ladefinición de E implica el uso de cargas de prueba lo suficientemente pequeñas (puntuales) como para que su influencia en el otro cuerpo sea despreciable.
1.- Las lineas comienzan en las cargas positivas dirigidas en todas direcciones y terminan en las cargas negativas, si la carga es solitaria entonces terminan en el infinito. Se dibujan de forma que la tangente a la linea de fuerza en cualquier punto coincida con la dirección del campo eléctrico E en ese punto.
Usemos las figuras 4, 5 y 6 para ilustrar lo que decimos.
En la figura 4 se representan las lineas de fuerza para dos cargas de igual magnitud pero de signo contrario. Esta configuración de cargas se denomina dipolo y en este caso la cantidad de lineas de fuerza que nacen en la carga positiva es igual a las que terminan en la carga negativa. En las regiones muy cercanas a las cargas, la lineas de fuerza son casi radiales y el pequeño espacio entre las lineas (alta densidad) indica un campo eléctrico fuerte en esas zonas.
En la figura 5 se muestran las lineas de fuerza en las proximidades de dos cargas iguales positivas. De la misma forma, las lineas son casi radiales en las zonas cercanas a las cargas y se han dibujado la misma cantidad de lineas de fuerza emergiendo de cada carga debido a que ambas son de la misma magnitud. Todas las lineas nacen en las cargas positivas, pero como no hay carga negativa, estas se extienden hasta el infinito. La lineas de fuerza no están próximas en la zona entre las cargas lo que indica que allí el campo eléctrico es débil.
Finalmente en la figura 6 se muestra la distribución de las lineas de fuerza para dos cargas de magnitud diferente y signo contrario, una +2q y la otra -q. Note que la cantidad de lineas de fuerza dibujadas en la carga +2q es el doble que las dibujadas en la carga -q. Evidentemente el exceso de lineas de fuerza que nacen en la carga positiva y no pueden encontrar su final en la carga negativa se extenderán hasta el infinito.
Una particularidad de las cargas eléctricas es que pueden ser de dos signos, y, que su signo determina la dirección de las fuerzas de interacción entre ellas. El átomo es eléctricamente neutro, los electrones tienen una carga que se ha convenido en asumir negativa, mientras el núcleo tiene una carga resultante de igual magnitud pero de signo contrario o positiva.
La evidencia que condujo al descubrimiento de las cargas eléctricas y de las fuerzas eléctricas depende más de las propiedades de la masa en su conjunto y solo indirectamente al hecho de que la materia está constituida por átomos. La propiedad más importante de los cuerpos para el caso que nos ocupa es su conductividad eléctrica, esto es, la facilidad con la que los electrones se pueden desplazar dentro del material. En términos generales y sin entrar en exactitudes las propiedades eléctricas de los diferentes materiales los separan en dos grupos: aquellos en los que las cargas negativas (electrones) se trasladan con facilidad y que se denominan conductores y los que el movimiento de los electrones es difícil, losaisladores.
Cuando frotamos un material aislador con otro del mismo tipo, por ejemplo, una varilla de teflón con un trozo de piel con sus pelos, la barra de teflón adquiere una carga eléctrica mientras que la piel adquiere una carga igual pero de sentido contrario. Esto hace suponer que se han transferido electrones de un cuerpo al otro y por lo tanto se ha perdido la neutralidad. En realidad, en el experimento, el teflón ha quedado con un exceso de electrones, está cargado negativamente y la piel con una deficiencia por lo que su carga será positiva, pero recuerde que esto es convencional por lo que es irrelevante para los resultados.
Ahora asumimos que tenemos una pequeña bola de corcho a la que transferimos la carga del teflón y otra, que hacemos lo mismo con las cargas del trozo de piel. Ambas bolas las colgamos de sendos hilos y las acercamos, el resultado será una fuerza de atracción entre ellas aun sin tocarse. Pero si transferimos a las dos bolas las cargas desde uno de los cuerpos, es decir del teflón o de la piel, al acercarlas se produce el efecto contrario se repelen, es decir en ambos casos hay una fuerza interactuando entre los cuerpos. Este comportamiento da la primera conclusión sobre los cuerpos cargados de electricidad:
Los cuerpos cargados con signo contrario se atraen, mientras que con el mismo signo se repelen.
El concepto de la acción a distancia, donde una fuerza podía actuar a través de un espacio abierto, incluso en el vacío, fue siempre difícil de aceptar. La acción a distancia sugería que de alguna manera debía llegar la fuerza creada por uno de los cuerpos al otro. Michael Faraday sugirió una vía para resolver esta dificultad, el primer cuerpo influye en el espacio que lo rodeaba por un campo que estaba presente, aunque el otro cuerpo existiera o no, dando origen al concepto de campo eléctrico. En la figura 1 se muestra una visualización del campo eléctrico usando hilos muy finos que flotan en aceite alrededor de una pequeña esfera cargada.
Observe que los hilos se orientan radialmente a la esferita cargada representada en negro en el centro, lo que indica que el campo eléctrico es radial y uniforme en todas direcciones (en la figura se ve en un plano pero en realidad es tridimensional). La orientación de los hilos sugirió un concepto muy útil, las lineas de fuerza. Es decir, se supuso que del centro del cuerpo cargado partían en todas direcciones unas lineas que representaban una fuerza y por lo tanto con una dirección definida. Se asumió dirigidas hacia afuera las lineas de fuerza que salen de un cuerpo cargado positivo y hacia adentro las de uno cargado negativo.
En resumen:
Un cuerpo cargado eléctricamente tiene a su alrededor un espacio de influencia que se denomina campo eléctrico y que al interactuar con otro cuerpo cargado adquiere la naturaleza de una fuerza.
Intensidad del campo eléctrico
Para definir la intensidad del campo eléctrico apoyémonos en la figura 2a, en ella se muestra un objeto con una carga positiva pequeña q0 en las inmediaciones de otro objeto cargado con una carga positiva grande Q. La intensidad del campo eléctrico (E) producido por Q en la localización de q0 se define como la magnitud de la fuerza que actúa sobre q0 (F) dividida por la magnitud de su carga.Figura 2. Interacción entre la carga de prueba y un cuerpo con una carga grande. Figura 3. Influencia de una carga de prueba grande. Figura 4. Figura 5. Figura 6. |
E ≡ ∣F∣ / ∣q0∣*
* Se usa el símbolo ≡ para indicar que es una definición. Los símbolos ∣...∣ se usan para indicar que se refiere solo a la magnitud sin tener en cuenta el signo.
La definición está referida a la magnitud (intensidad) del campo eléctrico cuya unidad en el sistema internacional (SI) es newton por coulomb (N/C), sin embargo, el campo eléctrico es una cantidad vectorial y:
La dirección del campo eléctrico en un punto se define como la dirección de la fuerza que se ejerce sobre una carga pequeña positiva colocada en ese punto.
Observe que E en la figura 2a, dada la definición, es horizontal y hacia la derecha. Sin embargo, en la figura 2b es horizontal y hacia la izquierda debido a que la carga pequeña positiva recibe una fuerza de atracción hacia el cuerpo con carga negativa grande.
Note algo importante, en ambos casos nos referimos a una carga de prueba pequeña y debe ser así para que la definición realmente funcione. Veamos:
Considere el uso de la esfera de prueba con carga q0 de la figura 3 colocada en el punto P en las inmediaciones del cuerpo que produce el campo eléctrico cuya intensidad queremos determinar, esta esfera de prueba con carga relativamente grande influye sobre la distribución de las cargas en la esfera que produce el campo eléctrico, y la consecuencia de esta reorganización es que la fuerza ejercida sobre la carga de prueba resulta diferente a lo que debía ser si no se hubieran reorganizado. Por lo tanto, la intensidad de campo eléctrico medido difiere del que existe en realidad en ausencia de la carga de prueba, lo que significa que ladefinición de E implica el uso de cargas de prueba lo suficientemente pequeñas (puntuales) como para que su influencia en el otro cuerpo sea despreciable.
Lineas de fuerza
Las lineas de fuerza en realidad son un artificio práctico que sirve para darle carácter físico tangible al espacio de influencia continuo que rodea un cuerpo cargado, pero esto no significa que el cuerpo cargado deba interpretarse como una suerte de erizo de mar del que parten lineas individuales entre las cuales no existe el campo eléctrico. Sin duda el concepto de lineas de fuerza fue una idea brillante de Faraday que permitió utilizar herramientas algebraicas para cuantificarlo numéricamente y darle una alternativa más cómoda a la representación visual.Propiedades de las lineas de fuerza
Las lineas de fuerza son lineas continuas direccionales en el espacio que están determinadas por el campo eléctrico de acuerdo a tres reglas simples:1.- Las lineas comienzan en las cargas positivas dirigidas en todas direcciones y terminan en las cargas negativas, si la carga es solitaria entonces terminan en el infinito. Se dibujan de forma que la tangente a la linea de fuerza en cualquier punto coincida con la dirección del campo eléctrico E en ese punto.
2.- El número de lineas que abandonan o llegan a una carga es proporcional a la magnitud de la carga, o lo que es lo mismo; la densidad espacial de lineas de fuerza alrededor de un punto en particular es proporcional a la intensidad del campo eléctrico en ese punto.
3.- Nunca las lineas de fuerza se cruzan.Usemos las figuras 4, 5 y 6 para ilustrar lo que decimos.
En la figura 4 se representan las lineas de fuerza para dos cargas de igual magnitud pero de signo contrario. Esta configuración de cargas se denomina dipolo y en este caso la cantidad de lineas de fuerza que nacen en la carga positiva es igual a las que terminan en la carga negativa. En las regiones muy cercanas a las cargas, la lineas de fuerza son casi radiales y el pequeño espacio entre las lineas (alta densidad) indica un campo eléctrico fuerte en esas zonas.
En la figura 5 se muestran las lineas de fuerza en las proximidades de dos cargas iguales positivas. De la misma forma, las lineas son casi radiales en las zonas cercanas a las cargas y se han dibujado la misma cantidad de lineas de fuerza emergiendo de cada carga debido a que ambas son de la misma magnitud. Todas las lineas nacen en las cargas positivas, pero como no hay carga negativa, estas se extienden hasta el infinito. La lineas de fuerza no están próximas en la zona entre las cargas lo que indica que allí el campo eléctrico es débil.
Finalmente en la figura 6 se muestra la distribución de las lineas de fuerza para dos cargas de magnitud diferente y signo contrario, una +2q y la otra -q. Note que la cantidad de lineas de fuerza dibujadas en la carga +2q es el doble que las dibujadas en la carga -q. Evidentemente el exceso de lineas de fuerza que nacen en la carga positiva y no pueden encontrar su final en la carga negativa se extenderán hasta el infinito.
Campo eléctrico y potencial de una carga puntual
El campo eléctrico de una carga puntual Q en un punto P distante r de la carga viene representado por un vector de- módulo
- dirección radial
- sentido hacia afuera si la carga es positiva, y hacia la carga si es negativa
Un campo eléctrico puede representarse por líneas de fuerza, líneas que son tangentes a la dirección del campo en cada uno de sus puntos.
En la figura, se representan las líneas de fuerza de una carga puntual, que son líneas rectas que pasan por la carga. Las equipotenciales son superficies esféricas concéntricas.
Campo eléctrico de un sistema de dos cargas eléctricas
Cuando varias cargas están presentes el campo eléctrico resultante es la suma vectorial de los campos eléctricos producidos por cada una de las cargas. Consideremos el sistema de dos cargas eléctricas de la figura.| El módulo del campo eléctrico producido por cada una de las cargas es Y las componentes del campo total son |
| Como el campo es tangente a las líneas de fuerza, la ecuación de las líneas de fuerza es tal como se muestra en la figura. |
Las superficies equipotenciales cortan perpendicularmente a las líneas de campo. Representaremos en el applet la intersección de las superficies equipotenciales con el plano XY.
La ecuación de las líneas equipotenciales es
La ley de Coulomb nos describe la interacción entre dos cargas eléctricas del mismo o de distinto signo. La fuerza que ejerce la carga Q sobre otra carga q situada a una distancia r es.
La fuerza F es repulsiva si las cargas son del mismo signo y es atractiva si las cargas son de signo contrario.
Concepto de campo
Es más útil, imaginar que cada uno de los cuerpos cargados modifica las propiedades del espacio que lo rodea con su sola presencia. Supongamos, que solamente está presente la carga Q, después de haber retirado la carga q del punto P. Se dice que la carga Q crea un campo eléctrico en el punto P. Al volver a poner la carga q en el punto P, cabe imaginar que la fuerza sobre esta carga la ejerce el campo eléctrico creado por la carga Q.| Cada punto P del espacio que rodea a la carga Q tiene una nueva propiedad, que se denomina campo eléctrico E que describiremos mediante una magnitud vectorial, que se define como la fuerza sobre la unidad de carga positiva imaginariamente situada en el punto P. |
La unidad de medida del campo en el S.I. de Unidades es el N/C
En la figura, hemos dibujado el campo en el punto P producido por una carga Q positiva y negativa respectivamente.
Energía potencial
La fuerza de atracción entre dos masas es conservativa, del mismo modo se puede demostrar que la fuerza de interacción entre cargas es conservativa.El trabajo de una fuerza conservativa, es igual a la diferencia entre el valor inicial y el valor final de una función que solamente depende de las coordenadas que denominamos energía potencial.
El trabajo infinitesimal es el producto escalar del vector fuerza F por el vector desplazamiento dl, tangente a la trayectoria.
dW=F·dl=F·dl·cosθ=F·dr.
donde dr es el desplazamiento infinitesimal de la partícula cargada q en la dirección radial.
Para calcular el trabajo total, integramos entre la posición inicial A, distante rA del centro de fuerzas y la posición final B, distante rB del centro fijo de fuerzas.
El trabajo W no depende del camino seguido por la partícula para ir desde la posición A a la posición B. La fuerza de atracción F, que ejerce la carga fija Q sobre la carga q esconservativa. La fórmula de la energía potencial es
El nivel cero de energía potencial se ha establecido en el infinito, para r=∞, Ep=0
El hecho de que la fuerza de atracción sea conservativa, implica que la energía total (cinética más potencial) de la partícula es constante, en cualquier punto de la trayectoria.Concepto de potencial
Del mismo modo que hemos definido el campo eléctrico, el potencial es una propiedad del punto P del espacio que rodea la carga Q. Definimos potencial V como la energía potencial de la unidad de carga positiva imaginariamente situada en P, V=Ep/q. El potencial es una magnitud escalar.La unidad de medida del potencial en el S.I. de unidades es el volt (V).
Relaciones entre fuerzas y campos
| Una carga en el seno de un campo eléctrico E experimenta una fuerza proporcional al campo cuyo módulo es F=qE, cuya dirección es la misma, pero el sentido puede ser el mismo o el contrario dependiendo de que la carga sea positiva o negativa. |
Relaciones entre campo y diferencia de potencial
La relación entre campo eléctrico y el potencial es.En la figura, vemos la interpretación geométrica. La diferencia de potencial es el área bajo la curva entre las posiciones A y B. Cuando el campo es constante
VA-VB=E·d que es el área del rectángulo sombreado.
El campo eléctrico E es conservativo lo que quiere decir que en un camino cerrado se cumple
Dado el potencial V podemos calcular el vector campo eléctrico E, mediante el operador gradiente.
Trabajo realizado por el campo eléctrico
El trabajo que realiza el campo eléctrico sobre una carga q cuando se mueve desde una posición en el que el potencial es VA a otro lugar en el que el potencial es VB es- El campo eléctrico realiza un trabajo W cuando una carga positiva q se mueve desde un lugar A en el que el potencial es alto a otro B en el que el potencial es más bajo. Siq>0 y VA>VB entonces W>0.
- El campo eléctrico realiza un trabajo cuando una carga negativa q se mueve desde un lugar B en el que el potencial es más bajo a otro A en el que el potencial es más alto.
- Una fuerza externa tendrá que realizar un trabajo para trasladar una carga positiva q desde un lugar B en el que el potencial es más bajo hacia otro lugar A en el que el potencial más alto.
- Una fuerza externa tendrá que realizar un trabajo para trasladar una carga negativa q desde un lugar A en el que el potencial es más alto hacia otro lugar B en el que el potencial más bajo.
El campo eléctrico es un campo físico que es representado mediante un modeloque describe la interacción entre cuerpos y sistemas con propiedades de naturalezaeléctrica.1 Se describe como un campo vectorial en el cual una carga eléctricapuntual de valor  sufre los efectos de una fuerza eléctrica
sufre los efectos de una fuerza eléctrica  dada por la siguiente ecuación:
dada por la siguiente ecuación:
 sufre los efectos de una fuerza eléctrica
sufre los efectos de una fuerza eléctrica  dada por la siguiente ecuación:
dada por la siguiente ecuación:(1)
En los modelos relativistas actuales, el campo eléctrico se incorpora, junto con elcampo magnético, en campo tensorial cuadridimensional, denominado campo electromagnético Fμν.2
Los campos eléctricos pueden tener su origen tanto en cargas eléctricas como encampos magnéticos variables. Las primeras descripciones de los fenómenos eléctricos, como la ley de Coulomb, solo tenían en cuenta las cargas eléctricas, pero las investigaciones de Michael Faraday y los estudios posteriores de James Clerk Maxwell permitieron establecer las leyes completas en las que también se tiene en cuenta la variación del campo magnético.
Esta definición general indica que el campo no es directamente medible, sino que lo que es observable es su efecto sobre alguna carga colocada en su seno. La idea de campo eléctrico fue propuesta por Faraday al demostrar el principio de inducción electromagnética en el año 1832.
La unidad del campo eléctrico en el SI es Newton por Culombio (N/C), Voltio por metro (V/m) o, en unidades básicas, kg·m·s−3·A−1 y la ecuación dimensional es MLT-3I-1.


 .
. por una distribución de carga
por una distribución de carga  en forma de diferencial de línea (
en forma de diferencial de línea (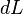 ), lo que produce un campo eléctrico
), lo que produce un campo eléctrico  .
.
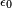 es la permitividad eléctrica del vacío, constante definida en el
es la permitividad eléctrica del vacío, constante definida en el  son las cargas que interactúan,
son las cargas que interactúan, es la distancia entre ambas cargas,
es la distancia entre ambas cargas, , es el vector de posición relativa de la carga 2 respecto a la carga 1.
, es el vector de posición relativa de la carga 2 respecto a la carga 1. es el
es el 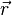 . Nótese que en la fórmula se está usando
. Nótese que en la fórmula se está usando 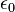 , esta es la permitividad en el vacío. Para calcular la interacción en otro medio es necesario cambiar la permitividad de dicho medio. (
, esta es la permitividad en el vacío. Para calcular la interacción en otro medio es necesario cambiar la permitividad de dicho medio. ( )
)
 , la que es una de las definiciones más conocidas acerca del campo eléctrico. Para una distribución continua de cargas el campo eléctrico viene dado por:
, la que es una de las definiciones más conocidas acerca del campo eléctrico. Para una distribución continua de cargas el campo eléctrico viene dado por:
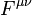 definido por un potencial cuadrivectorial de la forma:
definido por un potencial cuadrivectorial de la forma:
 es el
es el  es el
es el 
 es la
es la  es su
es su  la
la  , donde
, donde  es el diferencial de la posición definida
es el diferencial de la posición definida 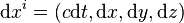 y
y  es la velocidad de la partícula, se obtiene:
es la velocidad de la partícula, se obtiene:


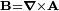 donde
donde  es el campo magnético; y por otro, el segundo representa la muy conocida descripción del campo como el gradiente de un potencial.
es el campo magnético; y por otro, el segundo representa la muy conocida descripción del campo como el gradiente de un potencial. se obtiene de la siguiente manera:
se obtiene de la siguiente manera:
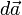 es el diferencial de área en dirección normal a la superficie. Aplicando la ecuación (
es el diferencial de área en dirección normal a la superficie. Aplicando la ecuación (
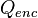 es la
es la 
 es la densidad volumétrica de carga. Esto indica que el campo eléctrico diverge hacia una distribución de carga; en otras palabras, que el campo eléctrico comienza en una carga y termina en otra.
es la densidad volumétrica de carga. Esto indica que el campo eléctrico diverge hacia una distribución de carga; en otras palabras, que el campo eléctrico comienza en una carga y termina en otra.




 , conocida como
, conocida como 
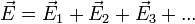


 y el observador en reposo respecto a la carga
y el observador en reposo respecto a la carga 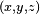 :
:


 es el ángulo formado por el vector de posición del punto donde se mide el campo (respecto a la carga) y la velocidad del movimiento. De esta última expresión se observa que si se considera una esfera de radio r alrededor de la carga el campo es más intenso en el "ecuador", tomando como polos norte y sur la interasección de la esfera con la trayectoria de la partícula, puede verse que el campo sobre la esfera varía entre un máximo
es el ángulo formado por el vector de posición del punto donde se mide el campo (respecto a la carga) y la velocidad del movimiento. De esta última expresión se observa que si se considera una esfera de radio r alrededor de la carga el campo es más intenso en el "ecuador", tomando como polos norte y sur la interasección de la esfera con la trayectoria de la partícula, puede verse que el campo sobre la esfera varía entre un máximo  y un mínimo
y un mínimo  dados por:
dados por:
![\bold{E} = \frac{1}{4\pi\epsilon} \left[
\frac{q(1-\frac{v^2}{c^2})}{(r-\frac{\bold{r}\cdot\bold{v}}{c})^3}(\bold{r}-\frac{\bold{v}}{c}r) +
\frac{q}{c^2(R-\frac{\bold{r}\cdot\bold{v}}{c})^3} \left[ \bold{r}
\times \left( (\bold{r}-\frac{\bold{v}}{c}r) \times \dot{\bold{v}} \right) \right]
\right]](https://upload.wikimedia.org/math/8/c/b/8cb721fac4318c480449c45573f049cc.png)
 y tiene una variación 1/R que representa la intensidad decreciente de una onda esférica de
y tiene una variación 1/R que representa la intensidad decreciente de una onda esférica de 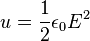
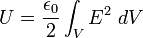
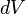 es el diferencial de volumen.
es el diferencial de volumen.
No hay comentarios:
Publicar un comentario