INGENIERÍA ELECTRÓNICA - CIRCUITOS ANALÓGICOS

 red eléctrica antimétrica es una red eléctrica que exhibe propiedades eléctricas anti- simétricas . El término se encuentra a menudo en la teoría de filtros , pero se aplica al análisis general de redes eléctricas . Antimétrico es el opuesto diametral de simétrico; no significa simplemente "asimétrico" (es decir, "carece de simetría"). Es posible que las redes sean simétricas o antimétricas en sus propiedades eléctricas sin ser física o topológicamente simétrica o antimétrica.

Definición [ editar ]

Figura 1. Ejemplos de simetría y antimetría: ambas redes son filtros de paso bajo pero una es simétrica (izquierda) y la otra es antimétrica (derecha). Para una escalera simétrica la primera elemento es igual a la n º, el segundo igual a la ( n -1) -ésima y así sucesivamente. Para una escalera antimétrica, el primer elemento es el dual de la n y así sucesivamente.

Las referencias a simetría y antimetría de una red generalmente se refieren a las impedancias de entrada ^{[nota 1]} de una red de dos puertos cuando se termina correctamente. ^{[nota 2]} Una red simétrica tendrá dos impedancias de entrada iguales, Z _i1 y Z _i2 . Para una red antimétrica, las dos impedancias deben ser la doble entre sí con respecto a alguna impedancia nominal R ₀ . Es decir, ^[1]

$${\ displaystyle {\ frac {Z_ {i1}} {R_ {0}}} = {\ frac {R_ {0}} {Z_ {i2}}}}

o equivalente

$${\ displaystyle Z_ {i1} Z_ {i2} = {R_ {0}} ^ {2}.}

Es necesario para la antimetría que las impedancias de terminación también sean duales entre sí, pero en muchos casos prácticos las dos impedancias de terminación son resistencias y ambas son iguales a la impedancia nominal R ₀ . Por lo tanto, ambos son simétricos y antimétricos al mismo tiempo. ^[1]

Antimetry física y eléctrica [ editar ]

Figura 2. Agregando otra sección en T a las escaleras de la figura 1

Figura 3. Ejemplos de redes simétricas (arriba) y antimétricas (abajo) que no exhiben simetría topológica ni antimetría.

Las redes simétricas y antimétricas a menudo también son topológicamente simétricas y antimétricas, respectivamente. La disposición física de sus componentes y valores es simétrica o antimétrica como en el ejemplo de escalera anterior. Sin embargo, no es una condición necesaria para la antimetría eléctrica. Por ejemplo, si las redes de ejemplo de la figura 1 tienen una sección en T idéntica adicional agregada al lado izquierdo como se muestra en la figura 2, entonces las redes permanecen topológicamente simétricas y antimétricas. Sin embargo, la red resultante de la aplicación del teorema de bisección de Bartlett ^[2]aplicados a la primera sección en T de cada red, como se muestra en la figura 3, no son ni físicamente simétricos ni antimétricos, sino que conservan sus propiedades eléctricas simétricas (en el primer caso) y antimétricas (en el segundo caso). ^[3]

Parámetros de dos puertos [ editar ]

Las condiciones para la simetría y la antimetría se pueden establecer en términos de parámetros de dos puertos . Para una red de dos puertos descrita por parámetros de impedancia ( z- parámetros ),

$${\ displaystyle z_ {11} = z_ {22}}

si la red es simétrica, y

$${\ displaystyle z_ {11} = - z_ {22}}

Si la red es antimétrica. Las redes pasivas del tipo ilustrado en este artículo también son recíprocas , lo que requiere que

$${\ displaystyle z_ {12} = z_ {21}}

y da como resultado una matriz de parámetros z de,

{\ displaystyle \ left [\ mathbf {z} \ right] = {\ begin {bmatrix} z_ {11} & z_ {12} \\ z_ {12} & z_ {11} \ end {bmatrix}}}

para redes simétricas y

{\ displaystyle \ left [\ mathbf {z} \ right] = {\ begin {bmatrix} z_ {11} & z_ {12} \\ z_ {12} & - z_ {11} \ end {bmatrix}}}

Para redes antimetricas. ^[4]

Para una red de dos puertos descrita por parámetros de dispersión ( parámetros S ),

$${\ displaystyle S_ {11} = S_ {22}}

si la red es simétrica, y

$${\ displaystyle S_ {11} = - S_ {22}}

Si la red es antimétrica. ^[5] La condición para la reciprocidad es,

$${\ displaystyle S_ {12} = S_ {21}}

dando como resultado una matriz de parámetros S de

{\ displaystyle \ left [\ mathbf {S} \ right] = {\ begin {bmatrix} S_ {11} & S_ {12} \\ S_ {12} & S_ {11} \ end {bmatrix}}}

para redes simétricas y

{\ displaystyle \ left [\ mathbf {S} \ right] = {\ begin {bmatrix} S_ {11} & S_ {12} \\ S_ {12} & - S_ {11} \ end {bmatrix}}}

Para redes antimetricas. ^[6]

Aplicaciones [ editar ]

Algunos diseños de circuitos producen naturalmente redes antimétricas. Por ejemplo, un filtro Butterworth depaso bajo implementado como una red de escalera con un número par de elementos será antimétrico. Del mismo modo, un paso de banda Butterworth con un número par de resonadores será antimétrico, al igual que un filtro mecánico Butterworth con un número par de resonadores mecánicos.

El modelo de ganancia asintótica ^[1] [2] (también conocido como el método de Rosenstark ^[3] ) es una representación de la ganancia de amplificadores de retroalimentación negativa dada por la relación de ganancia asintótica:

$${\ displaystyle G = G _ {\ infty} \ left ({\ frac {T} {T + 1}} \ right) + G_ {0} \ left ({\ frac {1} {T + 1}} \ right ) \,}

dónde $${\ displaystyle T}es la relación de retorno con la fuente de entrada deshabilitada (igual al negativo de la ganancia de bucle en el caso de un sistema de un solo bucle compuesto por bloques unilaterales ), G _∞ es la ganancia asintótica y G ₀ es el término de transmisión directa. Esta forma de ganancia puede proporcionar una visión intuitiva del circuito y, a menudo, es más fácil de obtener que un ataque directo a la ganancia.

Figura 1: Diagrama de bloques para el modelo de ganancia asintótica ^[4]

La Figura 1 muestra un diagrama de bloques que conduce a la expresión de ganancia asintótica. La relación de ganancia asintótica también se puede expresar como un gráfico de flujo de señal . Consulte la Figura 2. El modelo de ganancia asintótica es un caso especial del teorema del elemento adicional .

Figura 2: Posible gráfico de flujo de señal equivalente para el modelo de ganancia asintótica

Definición de términos [ editar ]

Como se deduce directamente de los casos limitantes de la expresión de ganancia, la ganancia asintótica G _∞ es simplemente la ganancia del sistema cuando la relación de retorno se acerca al infinito:

$${\ displaystyle G _ {\ infty} = G \ {\ Big |} _ {T \ rightarrow \ infty} \,}

mientras que el término de transmisión directa G ₀ es la ganancia del sistema cuando la relación de retorno es cero:

$${\ displaystyle G_ {0} = G \ {\ Big |} _ {T \ rightarrow 0} \.}

Ventajas [ editar ]

• Este modelo es útil porque caracteriza completamente los amplificadores de realimentación, incluidos los efectos de carga y las propiedades bilaterales de los amplificadores y las redes de realimentación.
• A menudo, los amplificadores de retroalimentación están diseñados de tal manera que la relación de retorno T es mucho mayor que la unidad. En este caso, y suponiendo que el término de transmisión directa G ₀ es pequeño (como suele ocurrir ), la ganancia G del sistema es aproximadamente igual a la ganancia asintótica G _∞ .
• La ganancia asintótica es (generalmente) solo una función de los elementos pasivos en un circuito, y a menudo se puede encontrar por inspección.
• La topología de realimentación (serie-serie, serie-derivación, etc.) no necesita identificarse de antemano ya que el análisis es el mismo en todos los casos.

Implementación [ editar ]

La aplicación directa del modelo implica estos pasos:

1. Seleccione una fuente dependiente en el circuito.
2. Encuentra la relación de retorno para esa fuente.
3. Encuentre la ganancia G _∞ directamente del circuito reemplazando el circuito con uno correspondiente a T= ∞.
4. Encuentre la ganancia G ₀ directamente del circuito reemplazando el circuito con uno correspondiente a T= 0.
5. Sustituye los valores de T, G _∞ y G ₀ en la fórmula de ganancia asintótica.

Estos pasos se pueden implementar directamente en SPICE utilizando el circuito de pequeña señal del análisis manual. En este enfoque, se puede acceder fácilmente a las fuentes dependientes de los dispositivos. Por el contrario, para las mediciones experimentales que usan dispositivos reales o simulaciones SPICE que usan modelos de dispositivos generados numéricamente con fuentes dependientes inaccesibles, la evaluación de la relación de retorno requiere métodos especiales .

Conexión con la teoría clásica de retroalimentación [ editar ]

La teoría de la retroalimentación clásica descuida el avance ( G ₀ ). Si se abandona feedforward, la ganancia del modelo de ganancia asintótica se convierte en

$${\ displaystyle G = G _ {\ infty} {\ frac {T} {1 + T}} = {\ frac {G _ {\ infty} T} {1 + {\ frac {1} {G _ {\ infty}} } G _ {\ infty} T}} \,}

mientras que en la teoría de retroalimentación clásica, en términos de la ganancia A de bucle abierto , la ganancia con retroalimentación (ganancia de bucle cerrado) es:

$${\ displaystyle A _ {\ mathrm {FB}} = {\ frac {A} {1 + {\ beta} _ {\ mathrm {FB}} A}} \.}

La comparación de las dos expresiones indica que el factor de realimentación β _FB es:

$${\ displaystyle \ beta _ {\ mathrm {FB}} = {\ frac {1} {G _ {\ infty}}} \,}

mientras que la ganancia de bucle abierto es:

$${\ displaystyle A = G _ {\ infty} \ T \.}

Si la precisión es adecuado (por lo general es), estas fórmulas sugieren una evaluación alternativa de T : evaluar la ganancia en lazo abierto y G _∞ y el uso de estas expresiones para encontrar T . A menudo, estas dos evaluaciones son más fáciles que la evaluación de T directamente.

Ejemplos [ editar ]

Los pasos para obtener la ganancia utilizando la fórmula de ganancia asintótica se describen a continuación para dos amplificadores de retroalimentación negativa. El ejemplo de un solo transistor muestra cómo funciona el método en principio para un amplificador de transconductancia, mientras que el segundo ejemplo de dos transistores muestra el enfoque de casos más complejos utilizando un amplificador de corriente.

Amplificador de transistor de una etapa [ editar ]

Figura 3: amplificador de realimentación FET

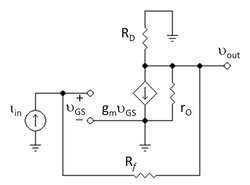
Considere la sencilla FET amplificador de realimentación en la Figura 3. El objetivo es encontrar el de baja frecuencia, de circuito abierto, transresistenciaganancia de este circuito G = v _fuera / i _en utilizando el modelo de ganancia asintótica.

Figura 4: Circuito de pequeña señal para amplificador transresistente; la resistencia de realimentación R _f se coloca debajo del amplificador para parecerse a la topología estándar

Figura 5: Circuito de pequeña señal con la ruta de retorno rota y el amplificador de voltaje de prueba en la interrupción

El circuito equivalente de pequeña señal se muestra en la Figura 4, donde el transistor se reemplaza por su modelo híbrido-pi .

Relación de retorno [ editar ]

Es más sencillo comenzar encontrando la relación de retorno T , porque G ₀ y G _∞ se definen como formas limitantes de la ganancia, ya que T tiende a cero o infinito. Para tomar estos límites, es necesario saber de qué parámetros depende T. Solo hay una fuente dependiente en este circuito, por lo que como punto de partida, la relación de retorno relacionada con esta fuente se determina como se describe en el artículo sobre la relación de retorno .

La relación de retorno se encuentra en la Figura 5. En la Figura 5, la fuente de corriente de entrada se establece en cero. Al cortar la fuente dependiente del lado de salida del circuito y cortocircuitar sus terminales, el lado de salida del circuito es aislado de la entrada y el bucle de retroalimentación se rompe. Una corriente de prueba i _treemplaza la fuente dependiente. Luego se encuentra la corriente de retorno generada en la fuente dependiente por la corriente de prueba. La relación de retorno es entonces T = - i _r / i _t . Usando este método, y notando que R _D está en paralelo con r _O , T se determina como:

$${\ displaystyle T = g _ {\ mathrm {m}} \ left (R _ {\ mathrm {D}} \ || r _ {\ mathrm {O}} \ right) \ approx g _ {\ mathrm {m}} R_ { \ mathrm {D}} \,}

donde la aproximación es exacta en el caso común donde r _O >> R _D . Con esta relación, está claro que los límites T → 0, o ∞ se realizan si permitimos la transconductancia g _m → 0, o ∞. ^[5]

Ganancia asintótica [ editar ]

Encontrar la ganancia asintótica G _∞ proporciona una visión y, por lo general, se puede hacer por inspección. Para encontrar G _∞dejamos g _m → ∞ y encontramos la ganancia resultante. La corriente de drenaje, i _D = g _m v _GS , debe ser finita. Por lo tanto, cuando g _{m se} aproxima al infinito, v _GS también debe aproximarse a cero. Como la fuente está conectada a tierra, v _GS = 0 implica v _G = 0 también. ^[6] Con v _G = 0 y el hecho de que toda la corriente de entrada fluye a través de R_f (como el FET tiene una impedancia de entrada infinita), el voltaje de salida es simplemente - i _en R _f . Por lo tanto

$${\ displaystyle G _ {\ infty} = {\ frac {v _ {\ mathrm {out}}} {i _ {\ mathrm {in}}}} = - R _ {\ mathrm {f}} \.}

Alternativamente, G _∞ es la ganancia que se encuentra al reemplazar el transistor por un amplificador ideal con ganancia infinita, un nulo . ^[7]

Alimentación directa [ editar ]

Para encontrar la alimentación directa. $${\ displaystyle G_ {0}}simplemente dejamos g _m → 0 y calculamos la ganancia resultante. Las corrientes a través de R _f y la combinación paralela de R _D || r _O , por lo tanto, debe ser igual e igual a i _en . Por lo tanto, la tensión de salida es i _en (R _D || r _O ) .

Por lo tanto

$${\ displaystyle G_ {0} = {\ frac {v_ {out}} {i_ {in}}} = R_ {D} \ | r_ {O} \ approx R_ {D} \,}

donde la aproximación es exacta en el caso común donde r _O >> R _D .

Ganancia general [ editar ]

La ganancia de transresistencia general de este amplificador es por lo tanto:

$${\ displaystyle G = {\ frac {v_ {out}} {i_ {in}}} = - R_ {f} {\ frac {g_ {m} R_ {D}} {1 + g_ {m} R_ {D }}} + R_ {D} {\ frac {1} {1 + g_ {m} R_ {D}}} = {\ frac {R_ {D} \ left (1-g_ {m} R_ {f} \ derecha)} {1 + g_ {m} R_ {D}}} \.}

Al examinar esta ecuación, parece ser ventajoso hacer que R _{D sea} grande para que la ganancia general se acerque a la ganancia asintótica, lo que hace que la ganancia sea insensible a los parámetros del amplificador ( g _m y R _D ). Además, un primer término grande reduce la importancia del factor de avance directo, que degrada el amplificador. Una forma de aumentar R _D es reemplazar esta resistencia por una carga activa , por ejemplo, un espejo de corriente .

Figura 6: amplificador de realimentación de dos transistores; cualquier impedancia de la fuente R _S se agrupa con la resistencia de base R _B .

Amplificador de transistor de dos etapas [ editar ]

Figura 7: Esquemas para usar el modelo de ganancia asintótica; parámetro α = β / (β + 1); resistencia R _C = R _C1 .

La Figura 6 muestra un amplificador de dos transistores con una resistencia de realimentación R _f . Este amplificador se refiere a menudo como una retroalimentación de la serie shunt amplificador, y se analizó en base a que la resistencia R ₂ está en serie con la corriente de salida de salida y las muestras, mientras que R _f está en derivación (paralela) con la entrada y la resta de la corriente de entrada. Vea el artículo sobre amplificador de retroalimentación negativa y referencias de Meyer o Sedra. ^[8] [9]Es decir, el amplificador utiliza retroalimentación actual. Con frecuencia, es ambiguo el tipo de retroalimentación involucrada en un amplificador, y el enfoque de ganancia asintótica tiene la ventaja / desventaja de que funciona, ya sea que usted entienda el circuito o no.

La Figura 6 indica el nodo de salida, pero no indica la elección de la variable de salida. En lo que sigue, la variable de salida se selecciona como la corriente de cortocircuito del amplificador, es decir, la corriente de colector del transistor de salida. Otras opciones para la salida se discuten más adelante.

Para implementar el modelo de ganancia asintótica, se puede usar la fuente dependiente asociada con cualquiera de los transistores. Aquí se elige el primer transistor.

Relación de retorno [ editar ]

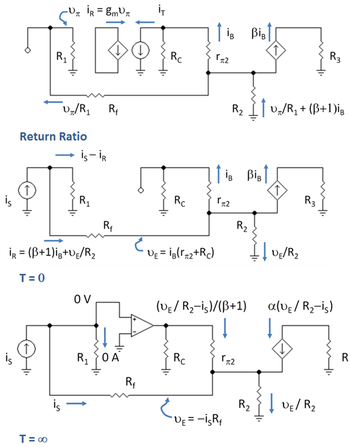
El circuito para determinar la relación de retorno se muestra en el panel superior de la Figura 7. Las etiquetas muestran las corrientes en las distintas ramas que se encuentran utilizando una combinación de la ley de Ohm y las leyes de Kirchhoff . Resistor R ₁ = R _B // r _π1 y R ₃ = R _C2 // R _L . KVL desde el suelo de R ₁ al suelo de R ₂proporciona:

$${\ displaystyle i _ {\ mathrm {B}} = - v _ {\ pi} {\ frac {1 + R_ {2} / R_ {1} + R _ {\ mathrm {f}} / R_ {1}} {( \ beta +1) R_ {2}}} \.}

KVL proporciona el voltaje del colector en la parte superior de R _C como

$${\ displaystyle v _ {\ mathrm {C}} = v _ {\ pi} \ left (1 + {\ frac {R _ {\ mathrm {f}}} {R_ {1}}} \ right) -i _ {\ mathrm {B}} r _ {\ pi 2} \.}

Por último, KCL en este colector proporciona

$${\ displaystyle i _ {\ mathrm {T}} = i _ {\ mathrm {B}} - {\ frac {v _ {\ mathrm {C}}} {R _ {\ mathrm {C}}}} \.}

Sustituyendo la primera ecuación en la segunda y la segunda en la tercera, la relación de retorno se encuentra como

$${\ displaystyle T = - {\ frac {i _ {\ mathrm {R}}} {i _ {\ mathrm {T}}}} = - g _ {\ mathrm {m}} {\ frac {v _ {\ pi}} {i _ {\ mathrm {T}}}}}

$${\ displaystyle = {\ frac {g _ {\ mathrm {m}} R _ {\ mathrm {C}}} {\ left (1 + {\ frac {R _ {\ mathrm {f}}} {R_ {1}} } \ right) \ left (1 + {\ frac {R _ {\ mathrm {C}} + r _ {\ pi 2}} {(\ beta +1) R_ {2}}} \ right) + {\ frac { R _ {\ mathrm {C}} + r _ {\ pi 2}} {(\ beta +1) R_ {1}}}}} \.}

Ganar G ₀ con T = 0 [ editar ]

El circuito para determinar G ₀ se muestra en el panel central de la Figura 7. En la Figura 7, la variable de salida es la corriente de salida β i _B (la corriente de carga de cortocircuito), que conduce a la ganancia de corriente de cortocircuito del Amplificador, es decir, β i _B / i _S :

$${\ displaystyle G_ {0} = {\ frac {\ beta i_ {B}} {i_ {S}}} \.}

Usando la ley de Ohm , el voltaje en la parte superior de R ₁ se encuentra como

$${\ displaystyle (i_ {S} -i_ {R}) R_ {1} = i_ {R} R_ {f} + v_ {E} \ \,}

o, reorganizando los términos,

$${\ displaystyle i_ {S} = i_ {R} \ left (1 + {\ frac {R_ {f}} {R_ {1}}} \ right) + {\ frac {v_ {E}} {R_ {1 }}} \.}

Usando KCL en la parte superior de R ₂ :

$${\ displaystyle i_ {R} = {\ frac {v_ {E}} {R_ {2}}} + (\ beta +1) i_ {B} \.}

El voltaje del emisor v _E ya se conoce en términos de i _B del diagrama de la Figura 7. Sustituyendo la segunda ecuación en la primera, i _B se determina en términos de i _S solo, y G _{0 se} convierte en:

$${\ displaystyle G_ {0} = {\ frac {\ beta} {(\ beta +1) \ left (1 + {\ frac {R_ {f}} {R_ {1}}} \ right) + (r_ { \ pi 2} + R_ {C}) \ left [{\ frac {1} {R_ {1}}} + {\ frac {1} {R_ {2}}} \ left (1 + {\ frac {R_ {f}} {R_ {1}}} \ right) \ right]}}}

La ganancia G ₀ representa el avance a través de la red de retroalimentación, y comúnmente es despreciable.

Gana G _∞ con T → ∞ [ editar ]

El circuito para determinar G _∞ se muestra en el panel inferior de la Figura 7. La introducción del amplificador operacional ideal (un nulo ) en este circuito se explica a continuación. Cuando T → ∞, la ganancia del amplificador también va a infinito, y en tal caso, la tensión diferencial que impulsa el amplificador (la tensión a través del transistor de entrada r _π1 ) se lleva a cero y (según la ley de Ohm cuando hay sin voltaje) no consume corriente de entrada. Por otro lado, la corriente de salida y la tensión de salida son lo que exige el circuito. Este comportamiento es como un nulo, por lo que se puede introducir un nulo para representar el transistor de ganancia infinita.

La ganancia actual se lee directamente del esquema:

$${\ displaystyle G _ {\ infty} = {\ frac {\ beta i_ {B}} {i_ {S}}} = \ left ({\ frac {\ beta} {\ beta +1}} \ right) \ left (1 + {\ frac {R_ {f}} {R_ {2}}} \ derecha) \.}

La comparación con la teoría clásica de retroalimentación [ editar ]

Usando el modelo clásico, se descuida el avance y el factor de realimentación β _FB es (asumiendo que el transistor β >> 1):

$${\ displaystyle \ beta _ {FB} = {\ frac {1} {G _ {\ infty}}} \ approx {\ frac {1} {(1 + {\ frac {R_ {f}} {R_ {2} }})}} = {\ frac {R_ {2}} {(R_ {f} + R_ {2})}} \,}

y la ganancia A de bucle abierto es:

$${\ displaystyle A = G _ {\ infty} T \ approx {\ frac {\ left (1 + {\ frac {R_ {f}} {R_ {2}}} \ right) g_ {m} R_ {C}} {\ left (1 + {\ frac {R_ {f}} {R_ {1}}} \ right) \ left (1 + {\ frac {R_ {C} + r _ {\ pi 2}} {(\ beta +1) R_ {2}}} \ right) + {\ frac {R_ {C} + r _ {\ pi 2}} {(\ beta +1) R_ {1}}}}} \.}

Ganancia general [ editar ]

Las expresiones anteriores se pueden sustituir en la ecuación del modelo de ganancia asintótica para encontrar la ganancia general G. La ganancia resultante es la ganancia actual del amplificador con una carga de cortocircuito.

Ganancia usando variables de salida alternativas [ editar ]

En el amplificador de la Figura 6, R _L y R _C2 están en paralelo. Para obtener la ganancia de transresistencia, digamos A _ρ , es decir, la ganancia que usa el voltaje como variable de salida, la ganancia de corriente de cortocircuito G se multiplica por R _C2 // R _L de acuerdo con la ley de Ohm :

$${\ displaystyle A _ {\ rho} = G \ left (R _ {\ mathrm {C2}} // R _ {\ mathrm {L}} \ right) \.}

La ganancia de voltaje en circuito abierto se encuentra en A _ρ configurando R _L → ∞.

Para obtener la ganancia de corriente cuando la corriente de carga i _L en la resistencia de carga R _L es la variable de salida, digamos A _i , se usa la fórmula para la división de corriente : i _L = i _out × R _C2 / (R _C2 + R _L ) y la ganancia de cortocircuito en corriente G se multiplica por este factor de carga :

$${\ displaystyle A_ {i} = G \ left ({\ frac {R_ {C2}} {R_ {C2} + R_ {L}}} \ right) \.}

Por supuesto, la ganancia de corriente de cortocircuito se recupera configurando R _L = 0 Ω.