INGENIERÍA ELECTRÓNICA - CIRCUITOS ANALÓGICOS

El teorema de bisección de Bartlett es un teorema eléctrico en el análisis de redes atribuido a Albert Charles Bartlett . El teorema muestra que cualquier red simétrica de dos puertos se puede transformar en una red de celosía . ^[1] El teorema a menudo aparece en la teoría del filtro, donde la red de celosía a veces se conoce como una sección X del filtro siguiendo la práctica común de la teoría del filtro de nombrar secciones después de las letras alfabéticas con las que se parecen.

El teorema según lo originalmente declarado por Bartlett requería que las dos mitades de la red fueran topológicamente simétricas. Wilhelm Cauer extendió el teorema para aplicarla a todas las redes que fueran eléctricamente simétricas. Es decir, la implementación física de la red no tiene ninguna relevancia. Solo se requiere que su respuesta en ambas mitades sea simétrica.

Aplicaciones [ editar ]

Los filtros de topología de celosía no son muy comunes. La razón de esto es que requieren más componentes (especialmente inductores ) que otros diseños. La topología de escalera es mucho más popular. Sin embargo, tienen la propiedad de ser intrínsecamente equilibrados y una versión equilibrada de otra topología , como las secciones en T, puede terminar usando más inductores. Una aplicación es para todos los pases.Filtros de corrección de fase en líneas de telecomunicaciones balanceadas. El teorema también hace una aparición en el diseño de filtros de cristal en las frecuencias de RF. Aquí, las topologías de escalera tienen algunas propiedades indeseables, pero una estrategia de diseño común es comenzar desde una implementación de escalera debido a su simplicidad. El teorema de Bartlett se usa luego para transformar el diseño a una etapa intermedia como un paso hacia la implementación final (usar un transformador para producir una versión desequilibrada de la topología de celosía). ^[3]

Definición y prueba [ editar ]

Definición [ editar ]

Comience con una red de dos puertos , N, con un plano de simetría entre los dos puertos . Luego, corte N a través de su plano de simetría para formar dos nuevos puertos idénticos, ½N. Conecte dos generadores de voltaje idénticos a los dos puertos de N. De la simetría se desprende claramente que ninguna corriente fluirá a través de ninguna rama que pase por el plano de simetría. La impedancia medida en un puerto de N en estas circunstancias será la misma que la medida si todas las ramas que pasaban por el plano de simetría estuvieran en circuito abierto. Por lo tanto, es la misma impedancia que la impedancia de circuito abierto de ½N. Llamemos a eso impedancia.$${\ displaystyle Z_ {oc}}.

Ahora considere la red N con dos generadores de voltaje idénticos conectados a los puertos pero con polaridad opuesta. Al igual que la superposición de corrientes a través de las ramas en el plano de simetría debe ser cero en el caso anterior, por analogía y aplicando el principio de dualidad , la superposición de voltajes entre nodos en el plano de simetría también debe ser cero en este caso. La impedancia de entrada es, por lo tanto, la misma que la impedancia de cortocircuito de ½N. Llamemos a eso impedancia.$${\ displaystyle Z_ {sc}}.

El teorema de bisección de Bartlett establece que la red N es equivalente a una red de celosía con series de ramas de $${\ displaystyle Z_ {sc}} y cruzar ramas de $${\ displaystyle Z_ {oc}}. ^[4]

Prueba [ editar ]

Considere la red de celosía que se muestra con generadores idénticos, E, conectados a cada puerto. De la simetría y la superposición se desprende que no fluye corriente en las ramas de la serie.$${\ displaystyle Z_ {sc}}. Esas ramas se pueden quitar y dejar el circuito abierto sin ningún efecto en el resto del circuito. Esto deja un circuito de circuito con un voltaje de 2E y una impedancia de$${\ displaystyle 2Z_ {oc}} dando una corriente en el bucle de;

$${\ displaystyle I = {\ frac {2E} {2Z_ {oc}}}}

y una impedancia de entrada de;

$${\ displaystyle {\ frac {E} {I}} = Z_ {oc}}

ya que se requiere que sea por equivalencia a los dos puertos originales.

De manera similar, revertir uno de los generadores resulta, mediante un argumento idéntico, en un bucle con una impedancia de $${\ displaystyle 2Z_ {sc}} y una impedancia de entrada de;

$${\ displaystyle {\ frac {E} {I}} = Z_ {sc}}

Recordando que estas configuraciones de generador son la forma precisa en que $${\ displaystyle Z_ {oc}} y $${\ displaystyle Z_ {sc}}Cuando se definieron en los dos puertos originales, se demostró que la red es equivalente para esos dos casos. Se demuestra que esto es así para todos los casos considerando que todas las demás condiciones de entrada y salida se pueden expresar como una superposición lineal de los dos casos ya probados.

Ejemplos [ editar ]

Rejilla equivalente a un filtro de paso alto de sección en T

Rejilla equivalente a un filtro de paso bajo de Zobel bridge-T

Es posible utilizar la transformación de Bartlett a la inversa; es decir, para transformar una red de celosía simétrica en alguna otra topología simétrica. Los ejemplos mostrados arriba podrían igualmente haberse mostrado al revés. Sin embargo, a diferencia de los ejemplos anteriores, el resultado no siempre es físicamente realizable con componentes pasivos lineales. Esto se debe a que existe la posibilidad de que la transformación inversa genere componentes con valores negativos. Las cantidades negativas solo pueden realizarse físicamente con componentes activos presentes en la red.

Ampliación del teorema [ editar ]

Ejemplo de impedancia y escala de frecuencia utilizando un prototipo de filtro de paso bajo de sección. En la primera transformación, el prototipo se divide en dos y la frecuencia de corte se vuelve a escalar de 1 rad / sa 10 ⁵  rad / s (15.9 kHz). En la segunda transformación, la red dividida se vuelve a escalar en el lado izquierdo para operar a 600 Ω y en el lado derecho para operar a 50 Ω.

Hay una extensión del teorema de Bartlett que permite modificar una red de filtro simétrico que opera entre terminaciones iguales de impedancia de entrada y salida para obtener impedancias de fuente y carga desiguales. Este es un ejemplo de escala de impedancia de un filtro prototipo . La red simétrica se divide en dos a lo largo de su plano de simetría. Una mitad es la escala de impedancia a la impedancia de entrada y la otra escala a la impedancia de salida. La forma de respuesta del filtro sigue siendo la misma. Esto no equivale a una coincidencia de impedanciaEn la red, las impedancias que miran a los puertos de la red no tienen relación con las impedancias de terminación. Esto significa que una red diseñada por el teorema de Bartlett, aunque tiene exactamente la respuesta de filtro predicha, también agrega una atenuación constante además de la respuesta de filtro. En las redes de adaptación de impedancia, un criterio de diseño habitual es maximizar la transferencia de potencia. La respuesta de salida es "la misma forma" en relación con el voltaje del generador ideal teórico que controla la entrada. No es lo mismo con respecto a la tensión de entrada real que es suministrada por el generador ideal teórico a través de su impedancia de carga. ^[5] [6]

La ganancia constante debida a la diferencia en las impedancias de entrada y salida viene dada por;

$${\ displaystyle A = {\ frac {V_ {2}} {E}} = {\ frac {2R_ {2}} {R_ {1} + R_ {2}}}}

Tenga en cuenta que es posible que esto sea mayor que la unidad, es decir, es posible una ganancia de voltaje, pero la potencia siempre se pierde.

La ecuación de Biryukov (o oscilador de Biryukov ), llamada Vadim Biryukov (1946), es una ecuación diferencial no lineal de segundo orden utilizada para modelar osciladores amortiguados . ^[1]

La ecuación está dada por

$${\ displaystyle {\ frac {d ^ {2} y} {dt ^ {2}}} + f (y) {\ frac {dy} {dt}} + y = 0, \ qquad \ qquad (1)}

donde ƒ ( y ) es una función constante por partes que es positiva, excepto por la pequeña y como

{\ displaystyle f (y) = {\ begin {cases} -F, & | y | \ leq Y_ {0}; \\ F, & | y |> Y_ {0}. \ end {cases}}}

{\ displaystyle F = {\ text {constant}}> 0, \ quad Y_ {0} = {\ text {constant}}> 0.}

Ec. (1) es un caso especial de la ecuación de Lienard ; Describe las auto-oscilaciones.

La solución (1) en intervalos de tiempo separados cuando f (y) es constante viene dada por ^[2]

$${\ displaystyle y_ {k} (t) = A_ {1, k} \ exp (s_ {1, k} t) + A_ {2, k} \ exp (s_ {2, k} t) \ qquad \ qquad (2)}

aquí $${\ displaystyle s_ {k} = F / 2 \ mp {\ sqrt {(F / 2) ^ {2} -1}}} , a {\ displaystyle | y |  y $${\ displaystyle s_ {k} = - F / 2 \ mp {\ sqrt {(F / 2) ^ {2} -1}}} de otra manera. La expresión (2) se puede utilizar para valores reales y complejos de$${\ displaystyle s_ {k}}.

La solución del primer semestre en $${\ displaystyle y (0) = \ pm Y_ {0}} es

Oscilaciones de relajación F = 4

{\ displaystyle y (t) = {\ begin {cases} y_ {1} (t), & 0 \ leq t

$${\ displaystyle y_ {1} (t) = A_ {1, k} \ cdot \ exp (s_ {1, k} t) + A_ {2, k} \ cdot \ exp (s_ {2, k} t) ,}

$${\ displaystyle y_ {2} (t) = A_ {3, k} \ cdot \ exp (s_ {3, k} t) + A_ {4, k} \ cdot \ exp (s_ {4, k} t) .}

La solución del segundo semestre es

{\ displaystyle y (t) = {\ begin {cases} -y_ {1} (tT / 2), & T / 2 \ leq t

La solución contiene cuatro constantes de integración. $${\ displaystyle A_ {1}}, $${\ displaystyle A_ {2}}, $${\ displaystyle A_ {3}}, $${\ displaystyle A_ {4}}, el período $${\ displaystyle T} y el límite $${\ displaystyle T_ {0}} Entre $${\ displaystyle y_ {1} (t)} y $${\ displaystyle y_ {2} (t)}necesita ser encontrado Una condición límite se deriva de la continuidad de$${\ displaystyle y (t)}) y $${\ displaystyle dy / dt}. ^[3]

La solución de (1) en el modo estacionario se obtiene resolviendo un sistema de ecuaciones algebraicas como

$${\ displaystyle y_ {1} (0) = - Y_ {0}}; $${\ displaystyle y_ {1} (T_ {0}) = Y_ {0}}; $${\ displaystyle y_ {2} (T_ {0}) = Y_ {0}}; $${\ displaystyle y_ {2} (T / 2) = Y_ {0}}; $${\ displaystyle \ left. {\ begin {matrix} dy_ {1} / dt \ end {matrix}} \ right | _ {T_ {0}} = \ left. {\ begin {matrix} dy_ {2} / dt \ end {matrix}} \ right | _ {T_ {0}}};$${\ displaystyle \ left. {\ begin {matrix} dy_ {1} / dt \ end {matrix}} \ right | _ {0} = - \ left. {\ begin {matrix} dy_ {2} / dt \ end {matrix}} \ right | _ {T / 2} \; \; \; (3)}.

Las constantes de integración se obtienen mediante el algoritmo de Levenberg-Marquardt . Con$${\ displaystyle f (y) = \ mu (-1 + y ^ {2})}, {\ displaystyle \ mu = const> 0}, Ec. (1) llamado oscilador de Van der Pol . Su solución no puede ser expresada por funciones elementales en forma cerrada.

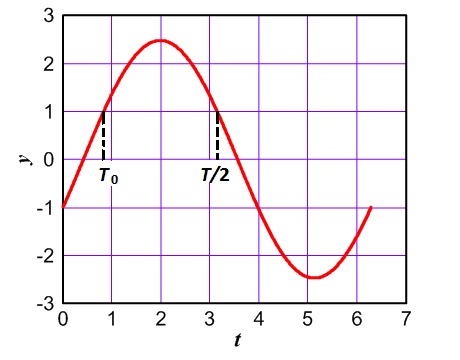
Oscilaciones sinusoidales F = 0.01