FÍSICA - CANTIDADES FÍSICAS

la velocidad angular se refiere a qué tan rápido un objeto gira o gira en relación con otro punto, es decir, qué tan rápido cambia la posición angular o la orientación de un objeto con el tiempo. Hay dos tipos de velocidad angular: velocidad angular orbital y velocidad angular de giro. La velocidad angular de giro se refiere a la rapidez con la que un cuerpo rígido gira con respecto a su centro de giro. La velocidad angular orbital se refiere a la rapidez con que el centro de rotación de un cuerpo rígido gira alrededor de un origen fijo, es decir, la tasa de tiempo de cambio de su posición angular con respecto al origen. En general, la velocidad angular se mide en ángulo por unidad de tiempo, radianes por segundo en unidades SI , y generalmente está representada por el símbolo omega (ω , a veces Ω ). Por convención, la velocidad angular positiva indica una rotación en sentido contrario a las agujas del reloj, mientras que la negativa es hacia la derecha.

Por ejemplo, un satélite geoestacionario completa una órbita por día sobre el ecuador, o 360 grados por 24 horas, y tiene una velocidad angular ω = 360/24 = 15 grados por hora, o 2π / 24 ≈ 0.26 radianes por hora. Si el ángulo se mide en radianes , la velocidad lineal es el radio multiplicado por la velocidad angular,$${\ displaystyle v = r \ omega}. Con un radio orbital a 42,000 km del centro de la Tierra, la velocidad del satélite a través del espacio es v = 42,000 × 0.26 ≈ 11,000 km / h. La velocidad angular es positiva ya que el satélite viaja hacia el este con la rotación de la Tierra (en sentido contrario a las agujas del reloj desde arriba del polo norte).

En tres dimensiones, la velocidad angular es un pseudovector , con su magnitud que mide la velocidad a la que un objeto gira o gira, y su dirección apuntando perpendicular al plano instantáneo de rotación o desplazamiento angular. La orientación de la velocidad angular se especifica convencionalmente por la regla de la mano derecha. 

Velocidad angular orbital de una partícula puntual [ editar ]

Partícula en dos dimensiones [ editar ]

La velocidad angular de la partícula en Pcon respecto al origen O está determinada por la componente perpendicular del vector de velocidad v .

En el caso más simple de movimiento circular en el radio r , con la posición dada por el desplazamiento angular$${\ displaystyle \ phi (t)} desde el eje x, la velocidad angular orbital es la velocidad de cambio del ángulo con respecto al tiempo: $${\ displaystyle \ omega = {\ tfrac {d \ phi} {dt}}}. Si$${\ displaystyle \ phi}se mide en radianes , la distancia desde el eje x alrededor del círculo a la partícula es$${\ displaystyle \ ell = r \ phi}, y la velocidad lineal es $${\ displaystyle v (t) = {\ tfrac {d \ ell} {dt}} = r \ omega (t)}, así que eso $${\ displaystyle \ omega = {\ tfrac {v} {r}}}.

En el caso general de una partícula que se mueve en el plano, la velocidad angular orbital es la velocidad a la que el vector de posición con respecto al origen elegido "arrastra" el ángulo. El diagrama muestra el vector de posición r desde el origen O hasta una partícula P , con sus coordenadas polares $${\ displaystyle (r, \ phi)}. (Todas las variables son funciones del tiempo t ). La partícula tiene una división de velocidad lineal como$${\ displaystyle \ mathbf {v} = \ mathbf {v} _ {\ |} + \ mathbf {v} _ {\ perp}}, con el componente radial $${\ displaystyle \ mathbf {v} _ {\ |}} paralelo al radio, y la componente radial transversal (o tangencial) $${\ displaystyle \ mathbf {v} _ {\ perp}}Perpendicular al radio. Cuando no hay un componente radial, la partícula se mueve alrededor del origen en un círculo; pero cuando no hay componente radial cruzado, se mueve en línea recta desde el origen. Como el movimiento radial no cambia el ángulo, solo la componente radial transversal de la velocidad lineal contribuye a la velocidad angular.

La velocidad angular ω es la tasa de cambio de la posición angular con respecto al tiempo, que se puede calcular a partir de la velocidad radial cruzada como:

$${\ displaystyle \ omega = {\ frac {d \ phi} {dt}} = {\ frac {v _ {\ perp}} {r}}.}

Aquí la velocidad radial cruzada. $${\ displaystyle v _ {\ perp}} es la magnitud firmada de $${\ displaystyle \ mathbf {v} _ {\ perp}}, positivo para el movimiento a la izquierda, negativo para el sentido de las agujas del reloj. Tomar coordenadas polares para la velocidad lineal v da la magnitud v (velocidad lineal) y el ángulo θ con respecto al vector del radio; en estos términos,$${\ displaystyle v _ {\ perp} = v \ sin (\ theta)}, así que eso

$${\ displaystyle \ omega = {\ frac {v \ sin (\ theta)} {r}}.

Estas fórmulas pueden ser derivadas de $${\ displaystyle \ mathbf {r} = (x (t), y (t))}, $${\ displaystyle \ mathbf {v} = (x '(t), y' (t))} y $${\ displaystyle \ phi = \ arctan (y (t) / x (t))}, junto con la fórmula de proyección. $${\ displaystyle v _ {\ perp} = {\ tfrac {\ mathbf {r} ^ {\ perp} \! \!} {r}} \ cdot \ mathbf {v}}, dónde $${\ displaystyle \ mathbf {r} ^ {\ perp} = (- y, x)}.

En dos dimensiones, la velocidad angular es un número con el signo más o menos que indica la orientación, pero no apunta en una dirección. El signo se toma convencionalmente como positivo si el vector del radio gira en sentido contrario a las agujas del reloj, y negativo si lo hace en el sentido de las agujas del reloj. La velocidad angular puede denominarse pseudoscalar , una cantidad numérica que cambia de signo bajo una inversión de paridad , como invertir un eje o cambiar los dos ejes.

De partículas en tres dimensiones [ editar ]

El vector de velocidad angular orbital codifica la tasa de tiempo de cambio de la posición angular, así como el plano instantáneo de desplazamiento angular. En este caso (movimiento circular en sentido contrario a las agujas del reloj) el vector apunta hacia arriba.

En el espacio tridimensional , nuevamente tenemos el vector de posición r de una partícula en movimiento. Aquí, la velocidad angular orbital es un pseudovector cuya magnitud es la velocidad a la que el vector de posición se desplaza hacia el ángulo y cuya dirección es perpendicular al plano instantáneo de desplazamiento angular. Sin embargo, como hay dos direcciones perpendiculares a cualquier plano, es necesaria una condición adicional para especificar de forma única la dirección de la velocidad angular; Convencionalmente, se usa la regla de la mano derecha .

Deja que el seudovector $${\ displaystyle \ mathbf {u}} sea ​​el vector unitario perpendicular al plano del desplazamiento angular instantáneo, de modo que la dirección instantánea del desplazamiento angular sea en sentido contrario a las agujas del reloj mirando desde la parte superior de $${\ displaystyle \ mathbf {u}}. Tomando coordenadas polares$${\ displaystyle (r, \ phi)} en este plano, como en el caso bidimensional anterior, uno puede definir el vector de velocidad angular orbital como:

$${\ displaystyle {\ boldsymbol {\ omega}} = \ omega \ mathbf {u} = {\ tfrac {d \ phi} {dt}} \ mathbf {u} = {\ frac {v \ sin (\ theta)} {r}} \ mathbf {u},}

donde θ es el ángulo entre r y v . En términos del producto cruzado, esto es:

$${\ displaystyle {\ boldsymbol {\ omega}} = {\ frac {\ mathbf {r} \ times \ mathbf {v}} {r ^ {2}}}.}

Tenga en cuenta que, según la definición del producto cruzado, el vector de velocidad angular orbital $${\ displaystyle {\ boldsymbol {\ omega}}} Siempre es perpendicular a ambos. $${\ displaystyle \ mathbf {r}} y $${\ displaystyle \ mathbf {v}}. A la inversa,$${\ displaystyle {\ boldsymbol {\ omega}}} define el plano en el que $${\ displaystyle \ mathbf {r}} y $${\ displaystyle \ mathbf {v}} mentira.

De la ecuación anterior, uno puede recuperar la velocidad tangencial como:

$${\ displaystyle \ mathbf {v} _ {\ perp} = {\ boldsymbol {\ omega}} \ times \ mathbf {r}}

Adición de vectores de velocidad angular [ editar ]

Construcción esquemática para la adición de vectores de velocidad angular para marcos rotativos

Si un punto gira con velocidad angular orbital $${\ displaystyle \ omega _ {1}}Sobre su centro de rotación en un marco de coordenadas. $${\ displaystyle F_ {1}} que a su vez gira con una velocidad angular de espín. $${\ displaystyle \ omega _ {2}} con respecto a un marco externo $${\ displaystyle F_ {2}}, podemos definir $${\ displaystyle \ omega _ {1} + \ omega _ {2}} para ser el vector de velocidad angular orbital compuesto del punto alrededor de su centro de rotación con respecto a $${\ displaystyle F_ {2}}. Esta operación coincide con la adición usual de vectores, y le da a la velocidad angular la estructura algebraica de un vector verdadero , en lugar de solo un pseudo-vector.

La única propiedad no obvia de la adición anterior es la conmutatividad . Esto se puede demostrar por el hecho de que el tensor de velocidad W(ver más abajo) es asimétrico, por lo que$${\ displaystyle R = e ^ {Wt}} Es una matriz de rotación que puede ser expandida como $${\ displaystyle R = I + W \ cdot dt + {\ tfrac {1} {2}} (W \ cdot dt) ^ {2} + \ ldots}. La composición de las rotaciones no es conmutativa, sino$${\ displaystyle (I + W_ {1} \ cdot dt) (I + W_ {2} \ cdot dt) = (I + W_ {2} \ cdot dt) (I + W_ {1} \ cdot dt)} es conmutativo a primer orden, y por lo tanto $${\ displaystyle \ omega _ {1} + \ omega _ {2} = \ omega _ {2} + \ omega _ {1}}.

Note que esto también define la resta como la adición de un vector negativo.

Girar vector de velocidad angular para un cuadro [ editar ]

Dado un marco giratorio de tres vectores de coordenadas de unidad, los tres deben tener la misma velocidad angular en cada instante. En dicho marco, cada vector puede considerarse como una partícula en movimiento con un radio escalar constante.

El marco giratorio aparece en el contexto de cuerpos rígidos , y se han desarrollado herramientas especiales para él: la velocidad angular de giro puede describirse como un vector o, de manera equivalente, como un tensor.

De acuerdo con la definición general, la velocidad angular de giro de un cuadro se define como la velocidad angular orbital de cualquiera de los tres vectores (la misma para todos) con respecto a su propio centro de rotación. La adición de vectores de velocidad angular para cuadros también se define por la adición de vectores habitual (composición de movimientos lineales), y puede ser útil para descomponer la rotación como en un cardán . Los componentes del vector se pueden calcular como derivados de los parámetros que definen los marcos en movimiento (ángulos de Euler o matrices de rotación). Como en el caso general, la suma es conmutativa:$${\ displaystyle \ omega _ {1} + \ omega _ {2} = \ omega _ {2} + \ omega _ {1}}.

Por el teorema de rotación de Euler , cualquier cuadro giratorio posee un eje de rotación instantáneo , que es la dirección del vector de velocidad angular, y la magnitud de la velocidad angular es consistente con el caso bidimensional.

Componentes de los vectores del marco [ editar ]

Considerando un vector de coordenadas del marco como una partícula, $${\ displaystyle \ mathbf {r} = \ mathbf {e} _ {i}} con $${\ displaystyle | \ mathbf {e} _ {i} | = 1}, obtenemos el vector de velocidad angular orbital:

$${\ displaystyle {\ boldsymbol {\ omega}} = {\ frac {\ mathbf {r} \ times \ mathbf {v}} {r ^ {2}}} = \ mathbf {e} _ {1} \ times { \ dot {\ mathbf {e}}} _ {1} = \ mathbf {e} _ {2} \ times {\ dot {\ mathbf {e}}} _ {2} = \ mathbf {e} _ {3 } \ times {\ dot {\ mathbf {e}}} _ {3}.}

aquí $${\ displaystyle \ mathbf {e} _ {i}} son las columnas de la matriz del marco, y $${\ displaystyle {\ dot {\ mathbf {e}}} _ {i}} Sus derivados del tiempo.

Componentes de los ángulos de Euler [ editar ]

Diagrama que muestra el marco de Euler en verde

Las componentes del pseudovector de velocidad angular de espín fueron calculadas por primera vez por Leonhard Euler utilizando sus ángulos de Euler y el uso de un marco intermedio:

• Un eje del marco de referencia (el eje de precesión)
• La línea de nodos del marco móvil con respecto al marco de referencia (eje de nutación)
• Un eje del cuadro móvil (el eje de rotación intrínseco)

Euler demostró que las proyecciones del pseudovector de velocidad angular en cada uno de estos tres ejes es la derivada de su ángulo asociado (que es equivalente a descomponer la rotación instantánea en tres rotaciones instantáneas de Euler ). Por lo tanto: ^[2]

$${\ displaystyle {\ boldsymbol {\ omega}} = {\ dot {\ alpha}} \ mathbf {u} _ {1} + {\ dot {\ beta}} \ mathbf {u} _ {2} + {\ punto {\ gamma}} \ mathbf {u} _ {3}}

Esta base no es ortonormal y es difícil de usar, pero ahora el vector de velocidad se puede cambiar al marco fijo o al marco en movimiento con solo un cambio de bases. Por ejemplo, cambiando al marco móvil:

$${\ displaystyle {\ boldsymbol {\ omega}} = ({\ dot {\ alpha}} \ sin \ beta \ sin \ gamma + {\ dot {\ beta}} \ cos \ gamma) \ mathbf {i} + ( {\ dot {\ alpha}} \ sin \ beta \ cos \ gamma - {\ dot {\ beta}} \ sin \ gamma) \ mathbf {j} + ({\ dot {\ alpha}} \ cos \ beta + {\ dot {\ gamma}}) \ mathbf {k}}

dónde $${\ displaystyle \ mathbf {i}, \ mathbf {j}, \ mathbf {k}}Son vectores unitarios para el cuadro fijo en el cuerpo móvil. Este ejemplo se ha realizado utilizando la convención ZXZ para los ángulos de Euler. ^[3]

Tensor de velocidad angular [ editar ]

Ver también: matriz simétrica sesgada.

El vector de velocidad angular. $${\ displaystyle {\ boldsymbol {\ omega}} = (\ omega _ {x}, \ omega _ {y}, \ omega _ {z})}lo definido anteriormente se puede expresar de manera equivalente como un tensor de velocidad angular , la matriz (o mapeo lineal) W = W ( t ) definida por:

{\ displaystyle W = {\ begin {pmatrix} 0 & - \ omega _ {z} & \ omega _ {y} omega _ {z} & 0 & - \ omega _ {x} \\ - \ omega _ {y } & \ omega _ {x} & 0 \\\ end {pmatrix}}}

Esta es una matriz de rotación infinitesimal . El mapeo lineal W actúa como$${\ displaystyle ({\ boldsymbol {\ omega}} \ times)}:

$${\ displaystyle {\ boldsymbol {\ omega}} \ times \ mathbf {r} = W \ cdot \ mathbf {r}.}

Cálculo a partir de la matriz de orientación [ editar ]

Un vector $${\ displaystyle \ mathbf {r}} realizar un movimiento circular uniforme alrededor de un eje satisface:

$${\ displaystyle {\ frac {d \ mathbf {r}} {dt}} = {\ boldsymbol {\ omega}} \ times \ mathbf {r} = W \ cdot \ mathbf {r}}

Dada la matriz de orientación A ( t ) de un cuadro, cuyas columnas son los vectores de coordenadas ortonormales móviles$${\ displaystyle \ mathbf {e} _ {1}, \ mathbf {e} _ {2}, \ mathbf {e} _ {3}}, podemos obtener su tensor de velocidad angular W ( t ) de la siguiente manera. La velocidad angular debe ser la misma para los tres vectores.$${\ displaystyle \ mathbf {r} = \ mathbf {e} _ {i}}Para organizar las tres ecuaciones vectoriales en columnas de una matriz, tenemos:

$${\ displaystyle {\ frac {dA} {dt}} = W \ cdot A.}

(Esto se mantiene incluso si A ( t ) no gira uniformemente). Por lo tanto, el tensor de velocidad angular es:

$${\ displaystyle W = {\ frac {dA} {dt}} \ cdot A ^ {{1} = {\ frac {dA} {dt}} \ cdot A ^ {\ mathrm {T}},}

Desde la inversa de la matriz ortogonal. $${\ displaystyle A} es su transposición $${\ displaystyle A ^ {\ mathrm {T}}}.

Propiedades de los tensores de velocidad angular [ editar ]

Ver también: Rotación infinitesimal.

En general, la velocidad angular en un espacio n -dimensional es la derivada del tiempo del tensor de desplazamiento angular, que es un tensor simétrico sesgado de segundo rango .

Este tensor W tendrá n ( n −1) / 2 componentes independientes, que es la dimensión del álgebra de Lie del grupode Lie de rotaciones de un espacio de producto interno n- dimensional. ^[4]

Dualidad con respecto al vector de velocidad [ editar ]

En tres dimensiones, la velocidad angular se puede representar mediante un pseudovector porque los tensores de segundo rango son duales a los pseudovectores en tres dimensiones. Dado que el tensor de velocidad angular W = W ( t ) es una matriz asimétrica sesgada :

{\ displaystyle W = {\ begin {pmatrix} 0 & \ omega _ {z} & - \ omega _ {y} \\ - \ omega _ {z} & 0 & \ omega _ {x} \\\ omega _ {y} & - \ omega _ {x} & 0 \\\ end {pmatrix}},}

Su Hodge dual es un vector, que es precisamente el vector de velocidad angular anterior.$${\ displaystyle {\ boldsymbol {\ omega}} = [\ omega _ {x}, \ omega _ {y}, \ omega _ {z}]}.

Exponencial de W [ editar ]

Si conocemos un cuadro inicial A (0) y nos dan un tensor de velocidad angular constante W , podemos obtener A( t ) para cualquier t dada . Recordemos la ecuación diferencial matricial:

$${\ displaystyle {\ frac {dA} {dt}} = W \ cdot A.}

Esta ecuación se puede integrar para dar:

$${\ displaystyle A (t) = e ^ {Wt} A (0),}

que muestra una conexión con el grupo de Lie de rotaciones.

W es antisimétrica [ editar ]

Probamos que el tensor de velocidad angular es asimétrico , es decir,$${\ displaystyle W = {\ frac {dA (t)} {dt}} \ cdot A ^ {\ text {T}}} satisface $${\ displaystyle W ^ {\ text {T}} = - W}.

Una matriz de rotación A es ortogonal, inversa a su transposición, por lo que tenemos$${\ displaystyle I = A \ cdot A ^ {\ text {T}}}. por$${\ displaystyle A = A (t)}Una matriz de cuadros, tomando el tiempo derivado de la ecuación da:

$${\ displaystyle 0 = {\ frac {dA} {dt}} A ^ {\ text {T}} + A {\ frac {dA ^ {\ text {T}}} {dt}}}

Aplicando la formula $${\ displaystyle (AB) ^ {\ text {T}} = B ^ {\ text {T}} A ^ {\ text {T}}},

$${\ displaystyle 0 = {\ frac {dA} {dt}} A ^ {\ text {T}} + \ left ({\ frac {dA} {dt}} A ^ {\ text {T}} \ right) ^ {\ text {T}} = W + W ^ {\ text {T}}}

Por lo tanto, W es el negativo de su transposición, lo que implica que es sesgado simétrico.

Descripción sin coordenadas [ editar ]

En cualquier instante $${\ displaystyle t}, el tensor de velocidad angular representa un mapa lineal entre el vector de posición $${\ displaystyle \ mathbf {r} (t)}y los vectores de velocidad $${\ displaystyle \ mathbf {v} (t)} de un punto sobre un cuerpo rígido que gira alrededor del origen:

$${\ displaystyle \ mathbf {v} = W \ mathbf {r}.}

La relación entre este mapa lineal y el pseudovector de velocidad angular. $${\ displaystyle \ omega} es el siguiente.

Debido a que W es el derivado de una transformación ortogonal , la forma bilineal

$${\ displaystyle B (\ mathbf {r}, \ mathbf {s}) = (W \ mathbf {r}) \ cdot \ mathbf {s}}

es sesgo-simétrico . Así podemos aplicar el hecho del álgebra exterior de que existe una forma lineal única. $${\ displaystyle L} en $${\ displaystyle \ Lambda ^ {2} V} ese

$${\ displaystyle L (\ mathbf {r} \ wedge \ mathbf {s}) = B (\ mathbf {r}, \ mathbf {s})}

dónde $${\ displaystyle \ mathbf {r} \ wedge \ mathbf {s} \ in \ Lambda ^ {2} V}es el producto exterior de$${\ displaystyle \ mathbf {r}} y $${\ displaystyle \ mathbf {s}}.

Tomando la aguda L ^♯ de L obtenemos

$${\ displaystyle (W \ mathbf {r}) \ cdot \ mathbf {s} = L ^ {\ sharp} \ cdot (\ mathbf {r} \ wedge \ mathbf {s})}

Presentando $${\ displaystyle \ omega: = {\ star} (L ^ {\ sharp})}, como el dual Hodge de L ^♯ , y aplicando la definición del dual Hodge dos veces, suponiendo que la unidad 3-vector preferida es$${\ displaystyle \ star 1}

$${\ displaystyle (W \ mathbf {r}) \ cdot \ mathbf {s} = {\ star} ({\ star} (L ^ {\ sharp}) \ wedge \ mathbf {r} \ wedge \ mathbf {s} ) = {\ star} (\ omega \ wedge \ mathbf {r} \ wedge \ mathbf {s}) = {\ star} (\ omega \ wedge \ mathbf {r}) \ cdot \ mathbf {s} = (\ omega \ times \ mathbf {r}) \ cdot \ mathbf {s},}

dónde

$${\ displaystyle \ omega \ times \ mathbf {r}: = {\ star} (\ omega \ wedge \ mathbf {r})}

por definición.

Porque $${\ displaystyle \ mathbf {s}}es un vector arbitrario, a partir de la no degeneración del producto escalar sigue

$${\ displaystyle W \ mathbf {r} = \ omega \ times \ mathbf {r}}

Velocidad angular como campo vectorial [ editar ]

Para la velocidad angular, el tensor asigna las posiciones a las velocidades, es un campo vectorial . En particular, este campo vectorial es un campo vectorial de Matanza que pertenece a un elemento del álgebra de Lie, por lo que (3) del grupo de rotación tridimensional SO (3) . Este elemento de tal (3) también puede considerarse como el vector de velocidad angular.

Consideraciones de cuerpos rígidos [ editar ]

Ver también: convenciones de ejes.

Posición del punto P ubicado en el cuerpo rígido (mostrado en azul). R _i es la posición con respecto al marco de laboratorio, centrado en O y r _i es la posición con respecto al marco de cuerpo rígido, centrado en O ' . El origen del bastidor de cuerpo rígido se encuentra en la posición vectorial R del bastidor de laboratorio.

Las mismas ecuaciones para la velocidad angular se pueden obtener razonando sobre un cuerpo rígidogiratorio . Aquí no se supone que el cuerpo rígido gira alrededor del origen. En cambio, se puede suponer que gira alrededor de un punto arbitrario que se mueve con una velocidad lineal V ( t ) en cada instante.

Para obtener las ecuaciones, es conveniente imaginar un cuerpo rígido unido a los marcos y considerar un sistema de coordenadas que esté fijo con respecto al cuerpo rígido. Luego estudiaremos las transformaciones de coordenadas entre esta coordenada y el sistema de "laboratorio" fijo.

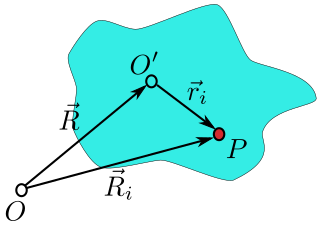
Como se muestra en la figura de la derecha, el origen del sistema de laboratorio está en el punto O , el origen del sistema de cuerpo rígido es en O ' y el vector de O a O 'es R . Una partícula ( i ) en el cuerpo rígido está ubicada en el punto P y la posición del vector de esta partícula es R _i en el marco del laboratorio, y en la posición r _i en el marco del cuerpo. Se ve que la posición de la partícula se puede escribir:

$${\ displaystyle \ mathbf {R} _ {i} = \ mathbf {R} + \ mathbf {r} _ {i}}

La característica definitoria de un cuerpo rígido es que la distancia entre dos puntos cualquiera en un cuerpo rígido no cambia en el tiempo. Esto significa que la longitud del vector$${\ displaystyle \ mathbf {r} _ {i}}es inmutable Por el teorema de rotación de Euler , podemos reemplazar el vector$${\ displaystyle \ mathbf {r} _ {i}} con $${\ displaystyle {\ mathcal {R}} \ mathbf {r} _ {io}} dónde $${\ displaystyle {\ mathcal {R}}}Es una matriz de rotación de 3 × 3 y$${\ displaystyle \ mathbf {r} _ {io}}es la posición de la partícula en algún punto fijo en el tiempo, digamos t = 0 . Este reemplazo es útil, porque ahora es solo la matriz de rotación.$${\ displaystyle {\ mathcal {R}}} Eso está cambiando en el tiempo y no el vector de referencia. $${\ displaystyle \ mathbf {r} _ {io}}, a medida que el cuerpo rígido gira alrededor del punto O ' . Además, como las tres columnas de la matriz de rotación representan los tres versores de un marco de referencia que gira junto con el cuerpo rígido, cualquier rotación sobre cualquier eje se vuelve ahora visible, mientras que el vector$${\ displaystyle \ mathbf {r} _ {i}}no giraría si el eje de rotación fuera paralelo a él, y por lo tanto solo describiría una rotación alrededor de un eje perpendicular a él (es decir, no vería la componente del pseudovector de velocidad angular paralela a él, y solo permitiría el cálculo del componente perpendicular a él). La posición de la partícula ahora se escribe como:

$${\ displaystyle \ mathbf {R} _ {i} = \ mathbf {R} + {\ mathcal {R}} \ mathbf {r} _ {io}}

Tomando el tiempo derivado se obtiene la velocidad de la partícula:

$${\ displaystyle \ mathbf {V} _ {i} = \ mathbf {V} + {\ frac {d {\ mathcal {R}}} {dt}} \ mathbf {r} _ {io}}

donde V _i es la velocidad de la partícula (en el marco de laboratorio) y V es la velocidad de O ′ (el origen del marco de cuerpo rígido). Ya que$${\ displaystyle {\ mathcal {R}}}Es una matriz de rotación, su inverso es su transposición. Así que sustituimos$${\ displaystyle {\ mathcal {I}} = {\ mathcal {R}} ^ {\ text {T}} {\ mathcal {R}}}:

$${\ displaystyle \ mathbf {V} _ {i} = \ mathbf {V} + {\ frac {d {\ mathcal {R}}} {dt}} {\ mathcal {I}} \ mathbf {r} _ { io}}

$${\ displaystyle \ mathbf {V} _ {i} = \ mathbf {V} + {\ frac {d {\ mathcal {R}}} {dt}} {\ mathcal {R}} ^ {\ text {T} } {\ mathcal {R}} \ mathbf {r} _ {io}}

$${\ displaystyle \ mathbf {V} _ {i} = \ mathbf {V} + {\ frac {d {\ mathcal {R}}} {dt}} {\ mathcal {R}} ^ {\ text {T} } \ mathbf {r} _ {i}}

o

$${\ displaystyle \ mathbf {V} _ {i} = \ mathbf {V} + W \ mathbf {r} _ {i}}

dónde $${\ displaystyle W = {\ frac {d {\ mathcal {R}}} {dt}} {\ mathcal {R}} ^ {\ text {T}}}Es el tensor de velocidad angular anterior .

Se puede demostrar que se trata de una matriz simétrica sesgada , por lo que podemos tomar su doble para obtener un pseudovector tridimensional que es precisamente el vector de velocidad angular anterior$${\ displaystyle {\ vec {\ omega}}}:

$${\ displaystyle {\ boldsymbol {\ omega}} = [\ omega _ {x}, \ omega _ {y}, \ omega _ {z}]}

Sustituyendo ω por W en la expresión de velocidad anterior, y reemplazando la multiplicación de matrices por un producto cruzado equivalente:

$${\ displaystyle \ mathbf {V} _ {i} = \ mathbf {V} + {\ boldsymbol {\ omega}} \ times \ mathbf {r} _ {i}}

Se puede ver que la velocidad de un punto en un cuerpo rígido se puede dividir en dos términos: la velocidad de un punto de referencia fijado en el cuerpo rígido más el término de producto cruzado que involucra la velocidad angular de la partícula con respecto al punto de referencia . Esta velocidad angular es el "spin" velocidad angular del cuerpo rígido en comparación con la velocidad angular del punto de referencia O ' sobre el origen O .

Consistencia [ editar ]

Hemos supuesto que el cuerpo rígido gira alrededor de un punto arbitrario. Debemos probar que la velocidad angular definida previamente es independiente de la elección del origen, lo que significa que la velocidad angular es una propiedad intrínseca del cuerpo rígido giratorio.

Demostrando la independencia de la velocidad angular de la elección del origen.

Vea el gráfico a la derecha: El origen del marco de laboratorio es O , mientras que O ₁ y O ₂ son dos puntos fijos en el cuerpo rígido, cuya velocidad es$${\ displaystyle \ mathbf {v} _ {1}} y $${\ displaystyle \ mathbf {v} _ {2}}respectivamente. Supongamos que la velocidad angular con respecto a O ₁ y O ₂ es$${\ displaystyle {\ boldsymbol {\ omega}} _ {1}} y $${\ displaystyle {\ boldsymbol {\ omega}} _ {2}}respectivamente. Dado que los puntos P y O ₂ tienen una sola velocidad,

$${\ displaystyle \ mathbf {v} _ {1} + {\ boldsymbol {\ omega}} _ {1} \ times \ mathbf {r} _ {1} = \ mathbf {v} _ {2} + {\ boldsymbol {\ omega}} _ {2} \ times \ mathbf {r} _ {2}}

$${\ displaystyle \ mathbf {v} _ {2} = \ mathbf {v} _ {1} + {\ boldsymbol {\ omega}} _ {1} \ times \ mathbf {r} = \ mathbf {v} _ { 1} + {\ boldsymbol {\ omega}} _ {1} \ times (\ mathbf {r} _ {1} - \ mathbf {r} _ {2})}

Los dos rendimientos anteriores que

$${\ displaystyle ({\ boldsymbol {\ omega}} _ {1} - {\ boldsymbol {\ omega}} _ {2}) \ times \ mathbf {r} _ {2} = 0}

Desde el punto P (y por lo tanto$${\ displaystyle \ mathbf {r} _ {2}}) es arbitrario, se deduce que

$${\ displaystyle {\ boldsymbol {\ omega}} _ {1} = {\ boldsymbol {\ omega}} _ {2}}

Si el punto de referencia es el eje de rotación instantáneo, la expresión de la velocidad de un punto en el cuerpo rígido tendrá el término de velocidad angular. Esto se debe a que la velocidad del eje de rotación instantáneo es cero. Un ejemplo de eje de rotación instantáneo es la bisagra de una puerta. Otro ejemplo es el punto de contacto de un cuerpo rígido esférico puramente rodante (o, más generalmente, convexo).