susceptibilidad eléctrica (; Latín : susceptibilis "receptivo") es una constante de proporcionalidad adimensional que indica el grado de polarización de un material dieléctrico en respuesta a un campo eléctrico aplicado . Cuanto mayor es la susceptibilidad eléctrica, mayor es la capacidad de un material para polarizarse en respuesta al campo, y por lo tanto reduce el campo eléctrico total dentro del material (y almacena energía). De este modo, la susceptibilidad eléctrica influye en la permitividad eléctrica del material y, por lo tanto, influye en muchos otros fenómenos en ese medio, desde la capacidad de los condensadores hasta la velocidad de la luz .
Definición de la susceptibilidad volumen [ editar ]
Susceptibilidad eléctrico se define como la constante de proporcionalidad (que puede ser un tensor ) en relación un campo eléctrico E a la inducida dieléctrica polarización eléctrica P tal que:
dónde
- es la densidad de polarización;
- es la permitividad eléctrica del espacio libre (constante eléctrica);
- Es la susceptibilidad eléctrica;
- Es el campo eléctrico.
Así que en el caso de un vacío:
Al mismo tiempo, el desplazamiento eléctrico D está relacionado con la densidad de polarización P por:
Con:
Polarizabilidad molecular [ editar ]
Existe un parámetro similar para relacionar la magnitud del momento dipolo p inducido de una moléculaindividual con el campo eléctrico local E que indujo el dipolo. Este parámetro es la polarizabilidad molecular ( α ), y el momento dipolar resultante del campo eléctrico local E local viene dado por:
Esto introduce una complicación, sin embargo, ya que localmente el campo puede diferir significativamente del campo aplicado en general. Tenemos:
donde P es la polarización por unidad de volumen, y N es el número de moléculas por unidad de volumen que contribuye a la polarización. Por lo tanto, si el campo eléctrico local es paralelo al campo eléctrico ambiental, tenemos:
Por lo tanto, solo si el campo local es igual al campo ambiente podemos escribir:
De lo contrario, uno debería encontrar una relación entre el campo local y el macroscópico. En algunos materiales, la relación Clausius-Mossotti se sostiene y se lee.
La ambigüedad en la definición [ editar ]
La definición de la polarizabilidad molecular depende del autor. En la definición anterior,
y están en unidades SI y la polarizabilidad molecular Tiene la dimensión de un volumen (m 3 ). Otra definición [3] sería mantener las unidades SI e integrar dentro :
En esta segunda definición, la polarizabilidad tendría la unidad SI de Cm 2 / V. Todavía existe otra definición [4]donde y se expresan en el sistema cgs y todavía se define como
Usando las unidades cgs da la dimensión de un volumen, como en la primera definición, pero con un valor que es inferior.
Susceptibilidad no lineal [ editar ]
En muchos materiales, la polarizabilidad comienza a saturarse en valores altos de campo eléctrico. Esta saturación puede ser modelada por una susceptibilidad no lineal . Estas susceptibilidades son importantes en la óptica no lineal y conducen a efectos como la segunda generación de armónicos (como la que se utiliza para convertir la luz infrarroja en luz visible, en punteros de láser verde ).
La definición estándar de susceptibilidades no lineales en unidades SI es a través de una expansión de Taylor de la reacción de polarización al campo eléctrico: [5]
(Excepto en materiales ferroeléctricos , la polarización incorporada es cero,.) El primer término de susceptibilidad, , corresponde a la susceptibilidad lineal descrita anteriormente. Si bien este primer término no tiene dimensiones, las susceptibilidades no lineales posteriorestiene unidades de (m / V) n -1 .
Las susceptibilidades no lineales pueden generalizarse a materiales anisotrópicos (donde cada susceptibilidad se convierte en un tensor de rango n + 1 ).
La dispersión y la causalidad [ editar ]
En general, un material no puede polarizarse instantáneamente en respuesta a un campo aplicado, por lo que la formulación más general en función del tiempo es
Es decir, la polarización es una convolución del campo eléctrico en momentos anteriores con una susceptibilidad dependiente del tiempo dada por. El límite superior de esta integral puede extenderse hasta el infinito también si se define para . Una respuesta instantánea corresponde a la susceptibilidad de la función delta de Dirac..
En un sistema lineal es más conveniente tomar la transformada de Fourier y escribir esta relación en función de la frecuencia. Debido al teorema de convolución , la integral se convierte en un producto,
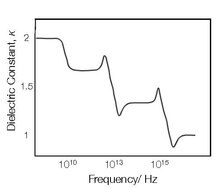
Esta dependencia de la frecuencia de la susceptibilidad conduce a la dependencia de la frecuencia de la permitividad. La forma de la susceptibilidad con respecto a la frecuencia caracteriza las propiedades de dispersión del material.
Además, el hecho de que la polarización solo puede depender del campo eléctrico en momentos anteriores (es decir, para ), una consecuencia de la causalidad , impone restricciones de Kramers-Kronigen la susceptibilidad.
Las medidas eléctricas son los métodos, dispositivos y cálculos utilizados para medir las cantidades eléctricas. La medición de las cantidades eléctricas se puede realizar para medir los parámetros eléctricos de un sistema. Usando transductores , las propiedades físicas como la temperatura, la presión, el flujo, la fuerza y muchos otros se pueden convertir en señales eléctricas, que luego pueden medirse y registrarse convenientemente. Las mediciones de alta precisión en el laboratorio de cantidades eléctricas se utilizan en experimentos para determinar propiedades físicas fundamentales como la carga del electróno la velocidad de la luz., y en la definición de las unidades para medidas eléctricas, con precisión en algunos casos del orden de unas pocas partes por millón. Se requieren medidas menos precisas todos los días en la práctica industrial. Las medidas eléctricas son una rama de la ciencia de la metrología .
Las cantidades eléctricas medibles independientes y semiindependientes comprenden:
- voltaje
- Corriente eléctrica
- Resistencia eléctrica y conductancia eléctrica.
- Reactancia eléctrica y susceptancia.
- Flujo magnético
- Carga eléctrica mediante electrómetro.
- Medición de descarga parcial
- Campo magnético mediante el sensor Hall.
- Campo eléctrico
- Electricidad mediante medidor de electricidad.
- Matriz S mediante el analizador de redes (eléctrico).
- Espectro de potencia eléctrica mediante analizador de espectro.
Las cantidades eléctricas dependientes medibles comprenden:
- Inductancia
- Capacidad
- Impedancia eléctrica definida como suma vectorial de resistencia eléctrica y reactancia eléctrica.
- La admisión eléctrica , el recíproco de la impedancia eléctrica.
- Fase entre corriente y voltaje y factor de potencia relacionado
- Densidad espectral electrica
- Ruido de la fase eléctrica
- Ruido de amplitud electrica
- Transconductancia
- Transimpedancia
- Ganancia de energía eléctrica
- Ganancia de voltaje
- Ganancia de corriente
- Frecuencia
- Retardo de propagación
La movilidad eléctrica es la capacidad de las partículas cargadas (como los electrones o los protones ) para moverse a través de un medio en respuesta a un campo eléctrico que las atrae. La separación de iones según su movilidad en fase gaseosa se denomina espectrometría de movilidad de iones , en fase líquida se llama electroforesis .
Teoría [ editar ]
Cuando una partícula cargada en un gas o líquido es activada por un campo eléctrico uniforme , se acelerará hasta que alcance una velocidad de deriva constante de acuerdo con la fórmula:
dónde
- es la velocidad de deriva ( unidades SI : ms −1 )
- es la magnitud del campo eléctrico aplicado (V m −1 )
- es la movilidad (m 2 V −1 s −1 )
En otras palabras, la movilidad eléctrica de la partícula se define como la relación entre la velocidad de deriva y la magnitud del campo eléctrico:
Por ejemplo, la movilidad del ion sodio (Na + ) en agua a 25 ° C es de 5,19 × 10 −8 m 2 V −1 s −1 . [1] Esto significa que un ión de sodio en un campo eléctrico de 1 V / m tendría una velocidad de deriva promedio de 5.19 × 10 −8m / s. Tales valores se pueden obtener a partir de mediciones de conductividad iónica en solución.
La movilidad eléctrica es proporcional a la carga neta de la partícula. Esta fue la base para la demostración de Robert Millikan de que las cargas eléctricas ocurren en unidades discretas, cuya magnitud es la carga del electrón .
La movilidad eléctrica también es inversamente proporcional al radio de Stokes. del ion, que es el radio efectivo del ion en movimiento, incluidas las moléculas de agua u otro disolvente que se mueven con él. Esto es cierto porque el ion solvatado se mueve a una velocidad de deriva constante Está sujeto a dos fuerzas iguales y opuestas: una fuerza eléctrica. y una fuerza de fricción , dónde es el coeficiente de fricción, Es la viscosidad de la solución. Para diferentes iones con la misma carga, como Li + , Na + y K +, las fuerzas eléctricas son iguales, por lo que la velocidad de deriva y la movilidad son inversamente proporcionales al radio a. [2] De hecho, las mediciones de conductividad muestran que la movilidad iónica aumenta de Li + a Cs +y, por lo tanto, el radio de Stokes disminuye de Li + a Cs + . Esto es lo opuesto al orden de los radios iónicos para los cristales, y muestra que en la solución los iones más pequeños (Li + ) están más hidratados.que el mayor (Cs + ). [2]
Movilidad en fase gaseosa [ editar ]
La movilidad se define para cualquier especie en la fase gaseosa, se encuentra principalmente en la física del plasma y se define como:
dónde
- es la carga de la especie,
- es la frecuencia de colisión de transferencia de impulso, y
- es la masa
La movilidad está relacionada con el coeficiente de difusión de la especie. a través de una ecuación exacta (requerida termodinámicamente) conocida como la relación de Einstein :
- ,
dónde
- es la constante de Boltzmann ,
- es la temperatura del gas , y
- Es una cantidad medida que puede ser estimada. Si uno define la ruta libre media en términos de transferencia de impulso , entonces obtiene:
- .
Pero tanto la ruta libre media de transferencia de momento como la frecuencia de colisión de transferencia de momento son difíciles de calcular. Se pueden definir muchos otros caminos libres medios. En la fase gaseosa,a menudo se define como la ruta libre media difusional, asumiendo que una relación aproximada simple es exacta:
- ,
dónde Es la masa de la especie difusora. Esta ecuación aproximada se vuelve exacta cuando se usa para definir la ruta libre media difusional.
Aplicaciones [ editar ]
La movilidad eléctrica es la base de la precipitación electrostática , utilizada para eliminar partículas de los gases de escape a escala industrial. Las partículas reciben una carga al exponerlas a iones de una descarga eléctricaen presencia de un campo fuerte. Las partículas adquieren una movilidad eléctrica y son conducidas por el campo a un electrodo colector.
Existen instrumentos que seleccionan partículas con un rango estrecho de movilidad eléctrica, o partículas con movilidad eléctrica más grande que un valor predefinido. [3] Los primeros se denominan generalmente "analizadores de movilidad diferencial". La movilidad seleccionada se identifica a menudo con el diámetro de una partícula esférica cargada individualmente, por lo que el "diámetro de movilidad eléctrica" se convierte en una característica de la partícula, independientemente de si es realmente esférica.
Pasar partículas de la movilidad seleccionada a un detector como un contador de partículas de condensaciónpermite medir la concentración en número de partículas con la movilidad actualmente seleccionada. Al variar la movilidad seleccionada a lo largo del tiempo, se pueden obtener datos de movilidad frente a la concentración. Esta técnica es aplicada en el escaneo de los medidores de partículas de movilidad .
























































No hay comentarios:
Publicar un comentario