INGENIERÍA ELECTRÓNICA - CIRCUITOS AÑALÓGICOS

Los filtros diseñados con la metodología de impedancia de imagen tienen un defecto peculiar en la teoría. Las características predichas del filtro se calculan asumiendo que el filtro termina con sus propias impedancias de imagen en cada extremo. Este no suele ser el caso; El filtro terminará con resistencias fijas. Esto hace que la respuesta del filtro se desvíe de lo teórico. Este artículo explica cómo se pueden tener en cuenta los efectos de las terminaciones finales del filtro de imagen .

En general, el efecto de las terminaciones es causar un redondeo de la respuesta de frecuencia en el corte. El método de imagen predice una discontinuidad aguda en la pendiente de la respuesta en el corte que no se realiza en la práctica, aunque un filtro de imagen bien diseñado puede acercarse a esto. Otra predicción del método de imagen es la pérdida cero en la banda de paso (suponiendo componentes ideales sin pérdida). Nuevamente, esto no se puede lograr en la práctica porque las reflexiones de las terminaciones finales siempre causan alguna pérdida.

Símbolos utilizados en este artículo [ editar ]

Impedancias [ editar ]

• $${\ displaystyle Z_ {I1} \, \!}La impedancia de la imagen al final 1.
• $${\ displaystyle Z_ {I2} \, \!} La impedancia de la imagen al final 2.
• $${\ displaystyle Z_ {I} \, \!} La impedancia de la imagen cuando ambos extremos son idénticos.
• $${\ displaystyle R_ {1} \, \!} La resistencia de terminación en el extremo 1.
• $${\ displaystyle R_ {2} \, \!} La resistencia de terminación en el extremo 2.
• $${\ displaystyle R \, \!} La resistencia de terminación cuando ambos extremos son idénticos.

Coeficientes [ editar ]

• $${\ displaystyle r_ {I1} \, \!}El coeficiente de reflexión al final 1.
• $${\ displaystyle r_ {I2} \, \!} El coeficiente de reflexión al final 2.
• $${\ displaystyle r_ {I} \, \!} El coeficiente de reflexión cuando ambos extremos son idénticos.
• $${\ displaystyle \ tau _ {I1} \, \!}El coeficiente de transmisión al final 1.
• $${\ displaystyle \ tau _ {I2} \, \!} El coeficiente de transmisión al final 2.
• $${\ displaystyle \ gamma \, \!}El complejo coeficiente de propagación del filtro.
• $${\ displaystyle \ alpha \, \!}El coeficiente de atenuación del filtro.
• $${\ displaystyle \ beta \, \!}El coeficiente de fase del filtro.

Tenga en cuenta que todos estos coeficientes se definen en relación con la impedancia de la imagen y no con la impedancia de entrada real del filtro.

Caso general [ editar ]

Un filtro de imagen arbitrario con terminaciones finales resistivas. Debido a que las terminaciones no son la impedancia de la imagen, la impedancia de entrada y salida no es Z _I1 y Z _I2 , ni el voltaje de entrada es V _i .

La función de transferencia de cualquier filtro conectado como se muestra en el diagrama anterior está dada por la expresión

$${\ displaystyle A (i \ omega) = {\ frac {V_ {o}} {V_ {i}}} = {\ sqrt {\ frac {Z_ {I2}} {Z_ {I1}}}} e ^ { - \ gamma} \ left [{\ frac {\ tau _ {I1} \ tau _ {I2}} {1-e ^ {- 2 \ gamma} r_ {I1} r_ {I2}}} \ right]}

dónde

$${\ displaystyle r_ {I1} = {\ frac {R_ {1} -Z_ {I1}} {R_ {1} + Z_ {I1}}}}

$${\ displaystyle r_ {I2} = {\ frac {R_ {2} -Z_ {I2}} {R_ {2} + Z_ {I2}}}}

$${\ displaystyle \ tau _ {I1} = {\ frac {2Z_ {I1}} {R_ {1} + Z_ {I1}}}}

$${\ displaystyle \ tau _ {I2} = {\ frac {2R_ {2}} {R_ {2} + Z_ {I2}}}}

Tenga en cuenta que V _i es el voltaje nominal que entregaría el generador si se terminara en su impedancia característica (es decir, R ₁ ), no aparece el voltaje real en los terminales de entrada del filtro.

Se puede observar además que la primera parte de la expresión,

$${\ displaystyle {\ sqrt {\ frac {Z_ {I2}} {Z_ {I1}}}} e ^ {- \ gamma}},

es la misma que la expresión para la función de transferencia sin tener en cuenta las terminaciones finales. La segunda parte de la expresión es, por lo tanto, la parte de la respuesta causada por las impedancias no coincidentes;

$${\ displaystyle \ left [{\ frac {\ tau _ {I1} \ tau _ {I2}} {1-e ^ {- 2 \ gamma} r_ {I1} r_ {I2}}} \ right].

Estuche simétrico [ editar ]

Cuando el filtro tiene impedancias y terminaciones de imagen simétricas , la expresión se puede reducir considerablemente. Tenga en cuenta que no hay ningún requisito para que el filtro sea simétricamente internamente, solo que las secciones finales tienen la misma impedancia de imagen enfrentada a impedancias de terminación idénticas.

$${\ displaystyle A (i \ omega) = e ^ {- \ gamma} \ left [{\ frac {4Z_ {I} R} {(R + Z_ {I}) ^ {2} -e ^ {- 2 \ gamma} (R-Z_ {I}) ^ {2}}} \ right]}

Se puede hacer una simplificación adicional si no hay pérdidas resistivas en el filtro (o se supone que son despreciables). En este caso, la impedancia de la imagen es puramente real ( R _I ) en la banda de paso y puramente imaginaria ( iX _I ) en la banda de parada. La magnitud de la función de transferencia está dada por

$${\ displaystyle \ left | A \ right | = {\ frac {1} {\ sqrt {1+ \ xi ^ {2}}}}}

donde para la banda de paso,

$${\ displaystyle \ xi = {\ frac {1} {2}} \ left ({\ frac {R_ {I}} {R}} - {\ frac {R} {R_ {I}}} \ right) \ pecado \ beta}

y para el stopband,

$${\ displaystyle \ xi = {\ frac {1} {2}} \ left ({\ frac {X_ {I}} {R}} - {\ frac {R} {X_ {I}}} \ right) \ sinh \ beta.}

Estuche antimetricos [ editar ]

Se puede hacer una simplificación similar para los filtros antimétricos sin pérdidas . En este caso la sustitución.

$${\ displaystyle Z_ {I1} Z_ {I2} = R_ {1} R_ {2} = R_ {o} ^ {2}}

Se hace en la ecuación general. Para la banda de paso,

$${\ displaystyle \ xi = {\ frac {1} {2}} \ left ({\ frac {R_ {I1}} {R}} - {\ frac {R} {R_ {I1}}} \ right) \ cos \ beta.}

y para el stopband,

$${\ displaystyle \ xi = {\ frac {1} {2}} \ left ({\ frac {X_ {I1}} {R}} - {\ frac {R} {X_ {I1}}} \ right) \ sinh \ beta.}

Antimétrico, en este contexto, significa que las impedancias y terminaciones de la imagen del filtro en cada extremo son las duales entre sí. Este será el caso si el filtro tiene una serie y una sección de derivación del mismo tipo, respectivamente, en cada extremo. Los filtros simétricos tienen un número par de medias secciones y los filtros antimétricos tienen un número impar de medias secciones. En la gran mayoría de los casos, el diseño del filtro será simétrico o antimétrico y se aplicará una de estas expresiones reducidas.

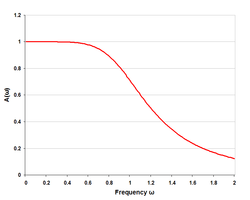
Algunos diagramas de respuesta de ejemplo [ editar ]

Respuesta teórica de un prototipo T-filtro de paso bajo correctamente terminado

Respuesta de un prototipo T-filtro de paso bajo con el efecto de las terminaciones terminales resistivas tomadas en cuenta

La respuesta del mismo filtro T con la respuesta teórica eliminada. Es decir, el componente de la respuesta se debe solo a los efectos de las terminaciones finales. La impedancia de imagen es un concepto utilizado en el diseño y análisis de redes electrónicas y, especialmente, en el diseño de filtros. El término impedancia de la imagen se aplica a la impedancia observada al mirar un puerto de una red. Por lo general , se implica una red de dos puertos, pero el concepto se puede extender a redes con más de dos puertos. La definición de impedancia de la imagen para una red de dos puertos es la impedancia, Z i 1 , observada mirando al puerto 1 cuando el puerto 2 termina con la impedancia de la imagen, Z i 2 , para el puerto 2. En general, las impedancias de imagen de los puertos 1 y 2 no serán iguales a menos que la red sea simétrica (o anti-simétrica) con respecto a los puertos. Derivación [ editar ] Red 'L' simple con impedancia en serie Z y admitancia en derivación Y. Se muestran las impedancias de imagen Z i 1 y Z i 2 Mostrando cómo se hace una sección en T a partir de dos medias secciones en L en cascada. Z i 2 se enfrenta a Z i 2 para proporcionar impedancias coincidentes Mostrando cómo se hace una sección a partir de dos medias L en cascada. Z i 1 se enfrenta a Z i 1 para proporcionar impedancias coincidentes A modo de ejemplo, a continuación se proporciona la derivación de las impedancias de imagen de una simple red 'L'. La red L consiste en una serie de impedancia , Z , y una derivación de admisión , Y . La dificultad aquí es que para encontrar Z i 1 primero es necesario terminar el puerto 2 con Z i 2 . Sin embargo, Z i 2también es un desconocido en esta etapa. El problema se resuelve al terminar el puerto 2 con una red idéntica: el puerto 2 de la segunda red está conectado al puerto 2 de la primera red y el puerto 1 de la segunda red se termina con Z i 1 . La segunda red está terminando la primera red en Z i 2según sea necesario. Matemáticamente, esto es equivalente a eliminar una variable de un conjunto de ecuaciones simultáneas. La red ahora se puede resolver para Z i 1 . Escribir la expresión para la impedancia de entrada da; $${\ displaystyle Z_ {i1} = Z + {\ frac {1} {2Y + {\ frac {1} {Z + Z_ {i1}}}}}} y resolviendo para $${\ displaystyle Z_ {i1}}, $${\ displaystyle Z_ {i1} ^ {2} = Z ^ {2} + {\ frac {Z} {Y}}} Z i 2 se encuentra por un proceso similar, pero es más sencillo trabajar en términos de reciprocidad, es decir, admisión de imágenes Y i 2 , $${\ displaystyle Y_ {i2} ^ {2} = Y ^ {2} + {\ frac {Y} {Z}}} Además, se puede ver en estas expresiones que las dos impedancias de la imagen están relacionadas entre sí por; $${\ displaystyle {\ frac {Z_ {i1}} {Y_ {i2}}} = {\ frac {Z} {Y}}} Medición [ editar ] La medición directa de la impedancia de la imagen mediante el ajuste de las terminaciones es un inconveniente iterativo y requiere componentes ajustables con precisión para efectuar la terminación. Una técnica alternativa para determinar la impedancia de imagen del puerto 1 es medir la impedancia de cortocircuito Z SC (es decir, la impedancia de entrada del puerto 1 cuando el puerto 2 está en cortocircuito) y la impedancia de circuito abierto Z OC (la entrada impedancia del puerto 1 cuando el puerto 2 está en circuito abierto). La impedancia de la imagen es dada entonces por, $${\ displaystyle Z_ {i1} = {\ sqrt {Z _ {\ mathrm {SC}} Z _ {\ mathrm {OC}}}}} Este método no requiere ningún conocimiento previo de la topología de la red que se está midiendo. Uso en diseño de filtro [ editar ] Cuando se utiliza en el diseño de filtros, la red 'L' analizada anteriormente se suele denominar media sección. Dos medias secciones en cascada formarán una sección T o una sección depending dependiendo de qué puerto de la sección L viene primero. Esto lleva a la terminología de Z i T a significar el Z i 1 en el análisis anterior y Z imean a significar Z i 2 . Relación con la impedancia característica [ editar ] La impedancia de la imagen es un concepto similar a la impedancia característica utilizada en el análisis de las líneas de transmisión . De hecho, en el caso límite de una cadena de redes en cascada en las que el tamaño de cada red única se aproxima a un elemento infinitamente pequeño, el límite matemático de la expresión de impedancia de la imagen es la impedancia característica de la cadena. Es decir, $${\ displaystyle Z_ {i} ^ {2} \ rightarrow {\ frac {Z} {Y}}} La conexión entre los dos se puede ver además al observar una definición alternativa, pero equivalente, de la impedancia de la imagen. En esta definición, la impedancia de la imagen de una red es la impedancia de entrada de una cadena infinitamente larga de redes idénticas en cascada (con los puertos dispuestos de tal manera que se enfrenta la impedancia similar). Esto es directamente análogo a la definición de impedancia característica como la impedancia de entrada de una línea infinitamente larga. A la inversa, es posible analizar una línea de transmisión con componentes agrupados , como uno que utiliza bobinas de carga , en términos de un filtro de impedancia de imagen. Función de transferencia [ editar ] La función de transferencia de la media sección, como la impedancia de la imagen, se calcula para una red terminada en sus impedancias de imagen (o, de manera equivalente, para una única sección en una cadena infinitamente larga de secciones idénticas) y viene dada por, $${\ displaystyle A (i \ omega) = {\ sqrt {\ frac {Z_ {I2}} {Z_ {I1}}}} e ^ {- \ gamma}} donde γ se denomina función de transmisión, función de propagación o parámetro de transmisión y viene dado por, $${\ displaystyle \ gamma = \ sinh ^ {- 1} {\ sqrt {ZY}}} los $${\ displaystyle {\ sqrt {\ frac {Z_ {I2}} {Z_ {I1}}}}término representa la relación de voltaje que se observaría si la potencia máxima disponible se transfiriera de la fuente a la carga. Sería posible absorber este término en la definición de γ , y en algunos tratamientos se toma este enfoque. En el caso de una red con impedancias de imagen simétricas, como una cadena de un número par de secciones L idénticas, la expresión se reduce a $${\ displaystyle A (i \ omega) = e ^ {- \ gamma} \, \!} En general, γ es un número complejo tal que, $${\ displaystyle \ gamma = \ alpha + i \ beta \, \!} La parte real de γ representa un parámetro de atenuación, α en nepers y la parte imaginaria representa un parámetro de cambio de fase, β en radianes . Los parámetros de transmisión para una cadena de n medias secciones, siempre que la impedancia similar siempre se enfrente, están dados por; $${\ displaystyle \ gamma _ {n} = n \ gamma \, \!} Al igual que con la impedancia de la imagen, los parámetros de transmisión se aproximan a los de una línea de transmisión cuando la sección del filtro se vuelve infinitamente pequeña, de modo que, $${\ displaystyle \ gamma \ rightarrow {\ sqrt {ZY}}} con α , β , γ , Z e Y, todos medidos ahora por metro en lugar de por media sección. Relación con los parámetros de red de dos puertos [ editar ] Parámetros ABCD [ editar ] Para una red recíproca ( AD - BC = 1 ), las impedancias de la imagen se pueden expresar [1] en términos de los parámetros ABCD como, $${\ displaystyle Z_ {I1} = {\ sqrt {\ frac {AB} {CD}}}} $${\ displaystyle Z_ {I2} = {\ sqrt {\ frac {DB} {CA}}}}. El término de propagación de la imagen, γ puede expresarse como, $${\ displaystyle \ gamma = \ cosh ^ {- 1} {\ sqrt {AD}}}. Tenga en cuenta que el término de propagación de la imagen para un segmento de línea de transmisión es equivalente a la constante de propagación de la línea de transmisión por la longitud.