MECÁNICA

La lubricación acústica o sónica se produce cuando el sonido (medible en un vacío al colocar un micrófono en un elemento del sistema deslizante) permite que la vibración introduzca separación entre las caras deslizantes. Esto podría ocurrir entre dos placas o entre una serie de partículas. La frecuencia de sonido requerida para inducir una vibración óptima y, por lo tanto, causa lubricación sónica, varía con el tamaño de las partículas (las frecuencias altas tendrán el efecto deseado, o no deseado, sobre la arena y las frecuencias más bajas tendrán este efecto sobre las rocas).

Ejemplos [ editar ]

Si hay un coeficiente de fricción dinámico entre dos objetos de 0.20, y la vibración hace que entren en contacto solo la mitad del tiempo, eso sería equivalente a un coeficiente de fricción constante de 0.10. ^{[ cita requerida ]} Esta reducción sustancial en la fricción puede tener un efecto profundo en el sistema. De acuerdo con una anécdota, las huellas de los tanques Panzer de la Segunda Guerra Mundial pueden haber sido lubricadas por su propio chirrido, lo que proporciona un ejemplo inesperado de lubricación acústica. ^[1]

Otro ejemplo ocurre durante los derrumbes. La mayoría de los deslizamientos no involucran este efecto, pero en ocasiones la frecuencia de las vibraciones causadas por el deslizamiento es óptima para hacer que los bloques vibren. En este caso, la retroalimentación hace que las rocas se deslicen mucho más lejos y más rápido que lo típico, lo que puede representar un peligro mayor para quienes se encuentran en su camino. Una característica notable de tal deslizamiento de tierra es que parece asemejarse al agua que fluye, o barro, y no a las rocas secas que se encontraban segundos antes. ^{[ cita requerida ]}

Aplicaciones [ editar ]

Además del estudio de deslizamientos de tierra, podría haber muchas otras aplicaciones para la lubricación acústica, particularmente cuando se requiere fricción variable o no se pueden usar lubricantes tradicionales. Un caso podría ser la perforación de pozos (para agua, petróleo, etc.) a través de arena. El tono óptimo del sonido (medición de la frecuencia) podría reducir considerablemente la fricción entre la broca y la arena. Nuevas maquinillas de afeitar con una cabeza vibrante también pueden ser un ejemplo.

En la ficción [ editar ]

• El protagonista en el videojuego Shadow Complex puede adquirir un "amortiguador de fricción" que utiliza lubricación acústica; esto le permite correr a velocidades muy altas.

La ecualización es un análisis matemático de los sistemas de anclaje de2 puntos que comparten la carga estática (también llamada distribución de carga) . Para aclarar, la ecualización es el método para encontrar tensión en dos cables que comparten una sola carga, pero con diferentes longitudes y ángulos a la carga.

Derivación [ editar ]

Considere el nodo, donde las dos patas de anclaje se unen con la línea principal. En este nodo, la suma de todas las fuerzas en la dirección x debe ser igual a cero ya que el sistema está en equilibrio mecánico . 

$${\ displaystyle F_ {x1} = F_ {x2} \,}

$${\ displaystyle F_ {1} \ sin (\ alpha) = F_ {2} \ sin (\ beta) \,}

$${\ displaystyle F_ {1} = F_ {2} {\ frac {\ sin (\ beta)} {\ sin (\ alpha)}} \,}

( 1 )

La fuerza neta en la dirección y también debe sumar cero. 

$${\ displaystyle F_ {y1} + F_ {y2} = F_ {cargar} \,}

$${\ displaystyle F_ {1} \ cos (\ alpha) + F_ {2} \ cos (\ beta) = F_ {load} \,}

( 2 )

Sustituir $${\ displaystyle F_ {1}}de la ecuación ( 1 ) a la ecuación ( 2 ) y factorizar$${\ displaystyle F_ {2}}. 

$${\ displaystyle F_ {2} {\ frac {\ sin (\ beta)} {\ sin (\ alpha)}} \ cos (\ alpha) + F_ {2} \ cos (\ beta) = F_ {load} \ ,}

$${\ displaystyle F_ {2} \ left [{\ frac {\ sin (\ beta)} {\ sin (\ alpha)}} \ cos (\ alpha) + \ cos (\ beta) \ right] = F_ {load } \,}

Resolver $${\ displaystyle F_ {2}} y simplificar.

$${\ displaystyle F_ {2} = {\ frac {F_ {load}} {\ left [{\ frac {\ sin (\ beta)} {\ sin (\ alpha)}} \ cos (\ alpha) + \ cos (\ beta) \ right]}} \,}

$${\ displaystyle F_ {2} = {\ frac {F_ {load}} {\ left [{\ frac {\ sin (\ beta) \ cos (\ alpha)} {\ sin (\ alpha)}} + {\ frac {\ cos (\ beta) \ sin (\ alpha)} {\ sin (\ alpha)}} \ right]}} \,}

$${\ displaystyle F_ {2} = {\ frac {F_ {load}} {\ left [{\ frac {\ cos (\ alpha) \ sin (\ beta) + \ sin (\ alpha) \ cos (\ beta) } {\ sin (\ alpha)}} \ right]}} \,}

$${\ displaystyle F_ {2} = F_ {load} {\ frac {\ sin (\ alpha)} {\ cos (\ alpha) \ sin (\ beta) + \ sin (\ alpha) \ cos (\ beta)} } \,}

Utilice una identidad trigonométrica para simplificar más y llegar a nuestra solución final para$${\ displaystyle F_ {2}}. 

$${\ displaystyle F_ {2} = F_ {load} {\ frac {\ sin (\ alpha)} {\ sin (\ alpha + \ beta)}} \,}

( 3 )

Entonces use $${\ displaystyle F_ {2}}de la ecuación ( 3 ) y sustitúyalo en ( 1 ) para resolver$${\ displaystyle F_ {1}}

$${\ displaystyle F_ {1} = F_ {load} {\ frac {\ sin (\ alpha)} {\ sin (\ alpha + \ beta)}} {\ frac {\ sin (\ beta)} {\ sin ( \ alpha)}} \,}

$${\ displaystyle F_ {1} = F_ {load} {\ frac {\ sin (\ beta)} {\ sin (\ alpha + \ beta)}} \,}

( 4 )

Ancla simétrica - Caso especial [ editar ]

Este diagrama muestra el caso específico cuando el ancla es simétrica. darse cuenta$${\ displaystyle 2 \ alpha = \ theta}.

Analicemos ahora un caso específico en el que los dos anclajes son "simétricos" a lo largo del eje y.

Comience notando $${\ displaystyle \ alpha} y $${\ displaystyle \ beta}son lo mismo. Empecemos por la ecuación ( 4 ) y sustituyamos$${\ displaystyle \ beta} para $${\ displaystyle \ alpha} y simplificar.

$${\ displaystyle F_ {eachAnchor} = F_ {load} {\ frac {Sin (\ alpha)} {Sin (\ alpha + \ alpha)}} \,}

$${\ displaystyle F_ {eachAnchor} = F_ {load} {\ frac {Sin (\ alpha)} {Sin (2 \ alpha)}} \,}

Y utilizando otra identidad trigonométrica podemos simplificar el denominador.

$${\ displaystyle F_ {eachAnchor} = F_ {load} {\ frac {Sin (\ alpha)} {2Sin (\ alpha) Cos (\ alpha)}} \,}

$${\ displaystyle F_ {eachAnchor} = {\ frac {F_ {load}} {2Cos (\ alpha)}} \,}

Tenga en cuenta que $${\ displaystyle \ alpha} es la mitad del angulo $${\ displaystyle \ theta}entre los dos puntos de anclaje. Para expresar la fuerza en cada ancla utilizando todo el ángulo.$${\ displaystyle \ theta}, sustituimos $${\ displaystyle \ alpha = \ theta / 2}.

$${\ displaystyle F_ {eachAnchor} = {\ frac {F_ {load}} {2Cos ({\ frac {\ theta} {2}})}} \,}

La carga está apuntando hacia abajo y está siendo sostenida por dos fuerzas que apuntan hacia arriba en varios ángulos. $${\ displaystyle \ alpha} y $${\ displaystyle \ beta}.

La mecánica aplicada (también mecánica de ingeniería ) es la rama de las ciencias físicas y la aplicación práctica de la mecánica . La mecánica pura describe la respuesta de cuerpos (sólidos y fluidos) o sistemas de cuerpos a fuerzas externas . Algunos ejemplos de sistemas mecánicos incluyen el flujo de un líquido bajo presión , la fractura de un sólido por una fuerza aplicada o la vibración de un oído en respuesta al sonido . Un practicante de la disciplina es conocido como un mecánico .

La mecánica aplicada describe el comportamiento de un cuerpo, ya sea en un estado inicial de reposo o de movimiento, sujeto a la acción de las fuerzas. ^[1] La mecánica aplicada, cierra la brecha entre la teoría física y su aplicación a la tecnología . Se utiliza en muchos campos de la ingeniería , especialmente la ingeniería mecánica y la ingeniería civil . En este contexto, se le conoce comúnmente como Mecánica de Ingeniería . Gran parte de la mecánica de ingeniería moderna se basa en las leyes de movimiento de Isaac Newton , mientras que la práctica moderna de su aplicación se remonta a Stephen Timoshenko., quien se dice que es el padre de la mecánica de ingeniería moderna.

Dentro de las ciencias prácticas, la mecánica aplicada es útil para formular nuevas ideas y teorías, descubrir e interpretar fenómenos y desarrollar herramientas experimentales y computacionales. En la aplicación de las ciencias naturales , se decía que la mecánica se complementaba con la termodinámica , el estudio del calor y, en general , la energía , y la electromecánica , el estudio de la electricidad y el magnetismo . 

En la práctica [ editar ]

Los avances e investigaciones en Mecánica Aplicada tienen una amplia aplicación en muchos campos de estudio. Algunas de las especialidades que ponen en práctica el tema son Ingeniería Mecánica , Ingeniería de la Construcción , Ciencia e Ingeniería de Materiales , Ingeniería Civil , Ingeniería Aeroespacial , Ingeniería Química, Ingeniería Eléctrica , Ingeniería Nuclear , Ingeniería Estructural y Bioingeniería . El profesor S. Marichamy dijo que "la mecánica es el estudio de los cuerpos que están en movimiento o en estado de reposo bajo la acción de las Fuerzas".

lista de segundos momentos de área de algunas formas. El segundo momento de área , también conocido como área de inercia, es una propiedad geométrica de un área que refleja cómo se distribuyen sus puntos con respecto a un eje arbitrario. La unidad de dimensión del segundo momento del área es la longitud a la cuarta potencia, L ⁴ , y no debe confundirse con el momento de inercia de masa . Sin embargo, si la pieza es delgada, el momento de inercia de masa es igual a la densidad de área por el momento de inercia de área.

Segundo momento del area [ editar ]

Descripción	Figura	Zona momento de inercia.	Comentario
Un área circular llena de radio r		$${\ displaystyle I_ {x} = {\ frac {\ pi} {4}} r ^ {4}} $${\ displaystyle I_ {y} = {\ frac {\ pi} {4}} r ^ {4}} $${\ displaystyle I_ {z} = {\ frac {\ pi} {2}} r ^ {4}} [1]	$${\ displaystyle I_ {z}}Es elmomento polar de inercia .
Un anillo de radio interior r 1y radio exteriorr 2		$${\ displaystyle I_ {x} = {\ frac {\ pi} {4}} \ left ({r_ {2}} ^ {4} - {r_ {1}} ^ {4} \ right)} $${\ displaystyle I_ {y} = {\ frac {\ pi} {4}} \ left ({r_ {2}} ^ {4} - {r_ {1}} ^ {4} \ right)} $${\ displaystyle I_ {z} = {\ frac {\ pi} {2}} \ left ({r_ {2}} ^ {4} - {r_ {1}} ^ {4} \ right)}	Para tubos delgados, $${\ displaystyle r \ equiv r_ {1} \ approx r_ {2}} y $${\ displaystyle r_ {2} \ equiv r_ {1} + t}.Entonces, para un tubo delgado,$${\ displaystyle I_ {x} = I_ {y} \ approx \ pi {r} ^ {3} {t}}. $${\ displaystyle I_ {z}}Es elmomento polar de inercia .
Un sector circular lleno de ángulo θ enradianes y radio r con respecto a un eje a través del centroide del sector y el centro del círculo		$${\ displaystyle I_ {x} = \ left (\ theta - \ sin \ theta \ right) {\ frac {r ^ {4}} {8}}}	Esta fórmula es válida solo para 0 ≤ $${\ displaystyle \ theta} ≤ $${\ displaystyle \ pi}
Un semicírculo relleno con radio r con respecto a una línea horizontal que pasa por el centroide del área		$${\ displaystyle I_ {x} = \ left ({\ frac {\ pi} {8}} - {\ frac {8} {9 \ pi}} \ right) r ^ {4} \ approx 0.1098r ^ {4 }} $${\ displaystyle I_ {y} = {\ frac {\ pi r ^ {4}} {8}}} [2]
Un semicírculo relleno como el anterior pero con respecto a un eje colineal con la base	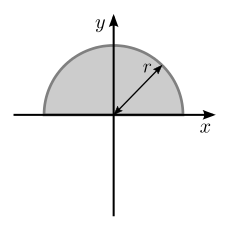	$${\ displaystyle I_ {x} = {\ frac {\ pi r ^ {4}} {8}}} $${\ displaystyle I_ {y} = {\ frac {\ pi r ^ {4}} {8}}} [2]	$${\ displaystyle I_ {x}}: Esto es una consecuencia del teorema del eje paralelo y el hecho de que la distancia entre los ejes x del anterior y este es$${\ displaystyle {\ frac {4r} {3 \ pi}}}
Un cuarto de círculo relleno con radio r con los ejes que pasan por las bases		$${\ displaystyle I_ {x} = {\ frac {\ pi r ^ {4}} {16}}} $${\ displaystyle I_ {y} = {\ frac {\ pi r ^ {4}} {16}}} [3]
Un cuarto de círculo relleno con radio r con los ejes que pasan por el centroide		$${\ displaystyle I_ {x} = \ left ({\ frac {\ pi} {16}} - {\ frac {4} {9 \ pi}} \ right) r ^ {4} \ approx 0.0549r ^ {4 }} $${\ displaystyle I_ {y} = \ left ({\ frac {\ pi} {16}} - {\ frac {4} {9 \ pi}} \ right) r ^ {4} \ approx 0.0549r ^ {4 }} [3]	Esto es una consecuencia del teorema del eje paralelo y el hecho de que la distancia entre estos dos ejes es$${\ displaystyle {\ frac {4r} {3 \ pi}}}
Una elipserellena cuyo radio a lo largo del eje x es a y cuyo radio a lo largo del eje yes b		$${\ displaystyle I_ {x} = {\ frac {\ pi} {4}} ab ^ {3}} $${\ displaystyle I_ {y} = {\ frac {\ pi} {4}} a ^ {3} b}
Un área rectangular rellena con un ancho de base de b y altura h	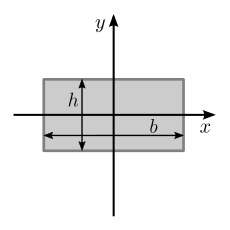	$${\ displaystyle I_ {x} = {\ frac {bh ^ {3}} {12}}} $${\ displaystyle I_ {y} = {\ frac {b ^ {3} h} {12}}} [4]
Un área rectangular rellena como la anterior pero con respecto a un eje colineal con la base.		$${\ displaystyle I_ {x} = {\ frac {bh ^ {3}} {3}}} $${\ displaystyle I_ {y} = {\ frac {b ^ {3} h} {3}}} [4]	Este es un resultado delteorema del eje paralelo.
Un rectángulohueco con un rectángulo interior cuyo ancho es b 1 y cuya altura esh 1		$${\ displaystyle I_ {x} = {\ frac {bh ^ {3} -b_ {1} {h_ {1}} ^ {3}} {12}}} $${\ displaystyle I_ {y} = {\ frac {b ^ {3} h- {b_ {1}} ^ {3} h_ {1}} {12}}}
Un área triangular rellena con un ancho de base de b , altura h y desplazamiento del vértice superior a , con respecto a un eje a través del centroide		$${\ displaystyle I_ {x} = {\ frac {bh ^ {3}} {36}}} $${\ displaystyle I_ {y} = {\ frac {b ^ {3} hb ^ {2} ha + bha ^ {2}} {36}}} [5]
Un área triangular rellena como la anterior pero con respecto a un eje colineal con la base.		$${\ displaystyle I_ {x} = {\ frac {bh ^ {3}} {12}}} $${\ displaystyle I_ {y} = {\ frac {b ^ {3} h + b ^ {2} ha + bha ^ {2}} {12}}} [5]	Esta es una consecuencia del teorema del eje paralelo.
Un ángulo de patas iguales, que se encuentra comúnmente en aplicaciones de ingeniería		$${\ displaystyle I_ {x} = I_ {y} = {\ frac {t (5L ^ {2} -5Lt + t ^ {2}) (L ^ {2} -Lt + t ^ {2})} { 12 (2L-t)}}} $${\ displaystyle I _ {(xy)} = {\ frac {L ^ {2} t (Lt) ^ {2}} {4 (t-2L)}}} $${\ displaystyle I_ {a} = {\ frac {t (2L-t) (2L ^ {2} -2Lt + t ^ {2})} {12}}} $${\ displaystyle I_ {b} = {\ frac {t (2L ^ {4} -4L ^ {3} t + 8L ^ {2} t ^ {2} -6Lt ^ {3} + t ^ {4}) } {12 (2L-t)}}}	$${\ displaystyle I _ {(xy)}} es el producto de inercia a menudo no utilizado, que se utiliza para definir la inercia con un eje girado
Un llenadohexágono regular con una longitud lateral de una		$${\ displaystyle I_ {x} = {\ frac {5 {\ sqrt {3}}} {16}} a ^ {4}} $${\ displaystyle I_ {y} = {\ frac {5 {\ sqrt {3}}} {16}} a ^ {4}}	El resultado es válido tanto para un eje horizontal como para uno vertical a través del centroide y, por lo tanto, también es válido para un eje con una dirección arbitraria que pasa por el origen.

Teorema del eje paralelo [ editar ]

Artículo principal: Teorema del eje paralelo.

El teorema del eje paralelo se puede usar para determinar el segundo momento del área de un cuerpo rígido sobre cualquier eje, dado el momento de inercia del cuerpo sobre un eje paralelo a través del centro de masa del objeto y la distancia perpendicular (d) entre los ejes.

$${\ displaystyle I_ {x '} = I_ {x} + Anuncio ^ {2}}